In questa guida spieghiamo cosa sono termini e funzioni in matematica.
Termini
Ogni espressione matematica costituita da costanti e i o variabili e (all’occasione) da segni di operazione, è per noi un termine.
Ad esempio, sono termini: 2, 3 • 4, 2n, a + bx, (a + b) (a – b), a + 2ab, ecc. Si badi, però, che in un termine non possono ricorrere né il segno ‘uguale’ (=), né il segno ‘minore’ (<), né il segno ‘maggiore’ (>).
Le espressioni 7 + 4 = 4 + 7 = 11, a + b = b + a, 5 < 7 o x > 10, non sono dunque termini. Tuttavia di ciò parleremo un po’ più avanti.
Funzioni ottenute per astrazione da termini
A) Supponiamo di avere il termine 2a, cioè il termine che designa un numero pari. Sostituiamo la variabile a con i numeri 1, 2, 3, .. . in ordine progressivo. Allora possiamo dire:
se si sostituisce I a a, allora si deve sostituire 2 a 2a;

B) Lo stesso vale anche per il termine a2, cioè per il termine che designa il quadrato di un numero. Anche qui possiamo dire:
se si sostituisce 1 a a, allora si deve sostituire 1 a a2;
C) Analogamente si ha col termine (a + 1) (a – 1), che designa il prodotto tra l’antecedente e il successivo di un determinato numero:
se si sostituisce 1I a a, allora si deve sostituire 0 a (a + 1) (a – 1);

D) La stessa operazione possiamo fare con il termine a2 -1 , che designa un numero minore di 1 rispetto a un quadrato:
se si sostituisce 1 a a, allora si deve sostituire 0 a a2 – 1;

Chiamiamo il valore da noi sostituito ad a nelle precedenti tabelle, argomento; chiamiamo funzione l’espressione costituita da a, dalle costanti e dai segni di operazione, nella quale sostituiamo l’argomento (vale a dire il termine visto in riferimento all’operazione di sostituzione); chiamiamo poi valore della funzione il risultato che si ottiene calcolando la funzione dopo la sostituzione di un determinato numero al posto di a.
Se, dunque, in un termine si sostituiscono al posto della variabile i numeri appartenenti al suo campo di variabilità uno dopo l’altro (e non un numero invariante anche se qualsiasi dello stesso campo di variabilità), si trasforma quel termine in una funzione.
Dopo quanto si è detto, si dovrebbe ammettere che `funzione’ o ‘termine’ sono la stessa cosa (se prescindiamo dal fatto che nel ‘termine’ 2a la lettera a designa un numero qualsiasi benché invariante, mentre nella `funzione’ 2a designa l’argomento percorrente l’intero campo di variabilità). Perché allora si usano due nomi diversi?
Il motivo di tale distinzione ci viene offerto dagli ultimi due esempi, C) e D). L’esempio C) contiene il termine (a + 1) (a – 1), l’esempio D) a2 – 1. Se ora prendiamo in considerazione l’andamento dei valori delle funzioni nei due esempi, si vede subito che esso è lo stesso, cioè per lo stesso argomento troviamo in ambedue gli esempi gli stessi valori delle funzioni.
La ragione di tale coincidenza sta nel fatto che ambedue i termini (a + 1) (a – 1) e a2 – 1 possono essere sostituiti l’uno con l’altro. Essi hanno infatti lo stesso valore, come si può facilmente dimostrare moltiplicando (a + 1) per (a – 1):
Se, dunque, si vogliono trovare i valori che corrispondono a determinati argomenti, è assolutamente indifferente la scelta del termine (a + 1) (a – 1) o di a2 – 1. In ogni caso, a partire dai medesimi argomenti si ottengono i medesimi valori. Infatti, il prodotto tra l’antecedente e il successore di un numero è sempre minore di un’unità rispetto al quadrato dello stesso numero.
Da quanto si è detto è facilmente intuibile perché si possa fare distinzione tra concetto di termine e concetto di funzione: due termini diversi possono rappresentare la stessa funzione, se essi sono sostituibili l’uno con l’altro in quanto coincidono nei rispettivi valori. Espressioni interscambiabili si dicono anche ‘equivalenti’ (con lo stesso valore).
Il concetto di ‘funzione’ è dunque un tipico concetto che si ottiene per astrazione: le funzioni sono astratte dai termini in quanto si prescinde dalla forma segnica dei termini e si confrontano soltanto i valori che se ne ottengono. Se ad argomenti uguali corrispondono valori uguali, si tratta della stessa funzione.
È necessario evidentemente confrontare tutti i valori. Non basta confrontare solo alcuni valori presi isolatamente. Cosi, ad esempio, i termini a, a2, a3, e a4, hanno tutti per l’argomento 0 il valore 0 e il valore 1 per l’argomento 1. Nonostante questo essi non rappresentano la stessa funzione, poiché i loro valori sono diversi per altri argomenti.
Con l’aiuto della retta numerica si può costruire una rappresentazione grafica bidimensionale della funzione per l’andamento dei valori nell’argomento e nella funzione. Si portano gli argomenti della funzione su una retta orizzontale e i valori della stessa funzione su una retta verticale. Per gli esempi sopra citati il grafico risulta
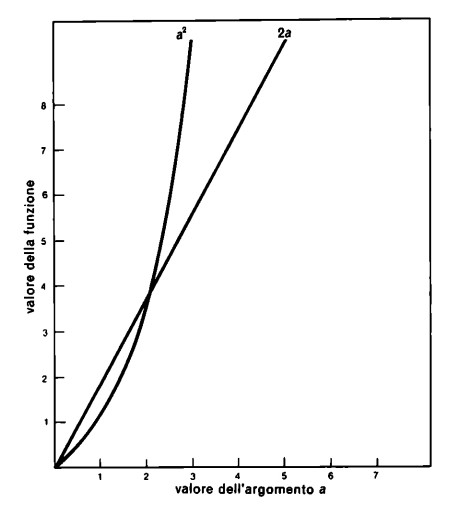
Tramite tale rappresentazione si tocca con mano il motivo per cui due termini interscambiabili rappresentano la stessa funzione: i punti dei grafici coincidono e pertanto non sono distinguibili.
Sulla base di considerazioni la cui discussione fuoriesce dall’ambito dei nostri interessi, è possibile, poi, unire sia i punti rappresentanti gli argomenti sia quelli rappresentanti i valori con una retta o una curva: almeno per ogni numero razionale a posto come argomento, esiste sempre un valore della funzione.
Le rette o curve che si ottengono unendo i punti rappresentanti gli argomenti e quelli rappresentanti i valori si chiamano grafici delle funzioni.
Normalmente per esprimere una funzione si usa il segno di uguaglianza. Ad esempio, dato il termine a2, si designa in genere con b il valore della funzione, che si ottiene sostituendo delle costanti al posto di a, il che si esprime attraverso le uguaglianze a2 = b o b = a2. Di solito, invece di a e b, si usano le lettere x e y; si arriva così alle uguaglianze: x2 = y ovvero y = x2.
Ancora, quando ci si riferisce alla rappresentazione grafica di una funzione, non si parla, solitamente, di argomeiti e valori ma semplicemente di valori x e valori y inseriti in un ‘sistema di coordinate’ costituito dall’asse orizzontale delle x e da quello verticale delle y
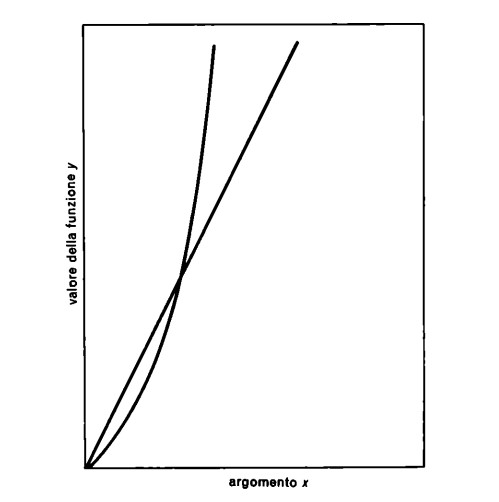
Contro questo modo di esprimere una funzione non vi sono obiezioni. Infatti è perfettamente lecito designare il termine, col quale si calcolano i valori della funzione, anche mediante una singola lettera b o y. Ciò nonostante, l’introduzione del segno di uguaglianza è fuorviante, dal momento che le funzioni sono definite mediante termini e i termini non contengono il segno di uguaglianza. E poi, per definire una funzione, abbiamo semplicemente associato agli argomenti, mediante i termini, determinati numeri, cioè i valori della funzione. Questa associazione, come tale, non richiede il segno di uguaglianza, ma solo il segno della ‘freccia’ per porre in evidenza la relazione tra argomenti e valori.
Per esprimere, dunque, la funzione astratta dal termine a2, non scriveremo più b = a2 o y = x2, ma semplicemente a → a2.
Il che significa: a ogni argomento a viene associato il rispettivo valore a2. Ce la possiamo cavare, pertanto, con un’unica lettera sia nell’argomento che nel valore.
È d’altra parte auspicabile poter designare il termine o – se prescindiamo dalla forma segnica del termine – la funzione, di cui devono essere calcolati i valori a partire dall’argomento a, con una lettera generica valida per tutti i casi.
Per questo motivo conveniamo di indicare in generale le espressioni 2a, a2, a + 1, (a + 1) (a – 1), a2 – 1, ecc. con il simbolo t o col simbolo ƒ, a seconda che quelle espressioni vengano intese rispettivamente come termini o come funzioni.
Di conseguenza, indicheremo in genere una funzione con l’espressione
![]()
dove a designa l’argomento, ƒ la funzione e ƒ(a) il valore della funzione, cioè il valore che assume la funzione qualora si sostituisce nel termine un determinato argomento al posto di a. Si deve dunque distinguere la funzione ƒ dal valore della funzione ƒ(a); la prima, infatti, è la funzione astratta da un termine contenente la variabile a, mentre il secondo è il valore da associare volta per volta ai singoli numeri a che fungono da argomenti.
Bisogna ancora osservare che una funzione è sempre univocamente determinata a destra, il che significa che a ogni argomento deve corrispondere uno e un solo valore, mentre lo stesso valore può essere associato a diversi argomenti. In altri termini: un argomento non può avere due valori diversi, mentre due diversi argomenti possono avere lo stesso valore.

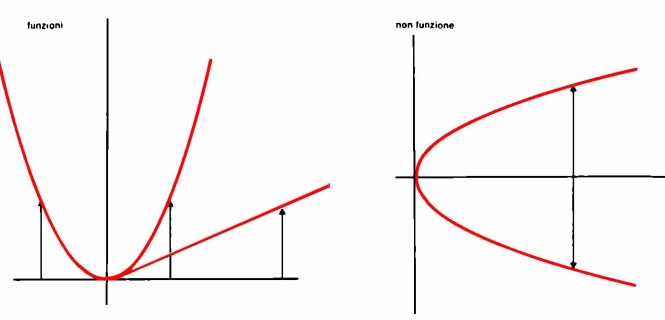
Ancora più chiaramente si può dimostrare l’univocità della funzione mediante il seguente grafico bidimensionale
Non ha importanza se due diversi argomenti, ovvero due diversi punti sull’asse orizzontale, hanno lo stesso valore (frecce verticali); al contrario, allo stesso argomento (punto sull’asse orizzontale) non possono corrispondere due valori (frecce verticali).
Esempi per funzioni univoche e non univoche possono essere quelli riportati qui di seguito.
a → a2 è una funzione univoca. Ogni numero a ha il suo quadrato (uno solo), mentre due numeri diversi, per esempio + a e – a, possono avere lo stesso quadrato. Infatti, il quadrato di + 3 e – 3 è sempre + 9.
Non univoca è la funzione inversa rispetto a a → a2, cioè a2 → a, ovvero a → √a. Infatti, ogni numero a possiede una radice quadrata positiva e una negativa, per esempio + 9 ha come radice sia + 3 che – 3.