In questa guida spieghiamo la proprietà commutativa e la proprietà associativa delle addizioni.

Nelle birrerie succede spesso di andare in compagnia. Spesso ci accompagnano amici ai quali paghiamo da bere. Per fare il conto, in questi casi, il cameriere prenderà il mio sottobicchiere e quello del mio compagno. Controllerà i segni che vi sono tracciati e dirà: « Quattro e tre fanno sette bicchieri di birra ». Che tipo di calcolo fa il cameriere? Di solito egli ragiona così: identifica la cifra I I I I del mio sottobicchiere e trova che si tratta di un ‘quattro’, identifica la cifra del sottobicchiere dell’amico e trova che si tratta di un ‘tre’. Poi dice (e questo lo sa a memoria): « Quattro e tre fanno sette ».
Il cameriere potrebbe procedere, però, anche diversamente. Potrebbe mettere i due sottobicchieri uno accanto all’altro e poi contare i trattini segnati su di essi passando direttamente dall’uno all’altro:

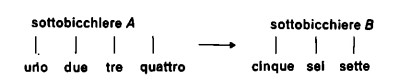
Se ‘contiamo insieme’ quattro e tre o, in altri termini, li sommiamo fra loro, si ottiene appunto sette. Ciò si può ulteriormente illustrare operando il seguente ordinamento:

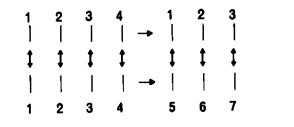
Si conta la medesima serie costituita da due gruppi di segni in due maniere diverse: la prima volta contando ogni gruppo a sé e la seconda volta passando direttamente da un gruppo all’altro. Siccome in ogni caso si ha il medesimo numero di segni (la qual cosa si dovrebbe sperimentare non soltanto con trattini segnati sulla carta, ma anche con pezzetti di legno o sassolini), si può dire:

o più brevemente:

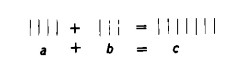
Con ciò abbiamo chiarito il concetto di addizione tra due cifre, ovvero due numeri.

L’addizione consiste nel contare i singoli segni di due cifre mediante un’unica operazione di conto, e non, come abbiamo fatto finora, con due operazioni separate.
Si possono naturalmente sommare numeri qualsiasi, grandi o piccoli che siano.
Per definire il concetto di addizione non bisogna, quindi, procedere per passi successivi in questo modo:

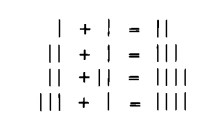
dal momento che le figure risultanti non sono ‘più semplici’ di una qualsiasi somma di figure | +| = ||, non è più facile da capire di ||| + | = ||||. Infatti, anche nel caso più semplice si deve passare da ‘uno’ e `uno’ a ‘uno, due’ e, una volta imparato a operare con numeri qualsiasi, ciò si può mostrare con una coppia qualsiasi di numeri grandi a piacere.

Commutatività

A questo punto è logico porsi una domanda. Quando il cameriere vuoi fare il conto, dovrà per forza prendere prima il sottobicchiere con quattro trattini e poi quello con tre, o potrà anche contare prima i tre bicchieri dell’amico ed aggiungervi poi i rimanenti quattro? In altri termini, è indifferente l’ordine di enumerazione dei bicchieri?
Naturalmente esso è indifferente; è l’esperienza pratica che ce lo dice. Sappiamo infatti che l’entità del conto non dipende mai dall’ordine che il cameriere segue nel sommare le singole consumazioni. Ciò nonostante, non è per niente evidente che nel caso della somma i numeri da sommare siano interscambiabili. Nell’ambito della matematica esistono molti esempi di operazioni in cui non è possibile invertire l’ordine dei numeri senza cambiare il risultato.
Per semplicità riportiamo un esempio non matematico. Le espressioni:
`il padre il cui fratello’,
`il fratello il cui padre’
non sono sinonime. Infatti il fratello del padre è lo zio, mentre il padre del fratello è il proprio padre: i fratelli hanno ovviamente lo stesso padre.

Per la medesima ragione dobbiamo ora dimostrare la interscambiabilità o commutatività dei numeri di cui si vuol trovare la somma. Innanzitutto sommiamo due numeri nel seguente ordine:

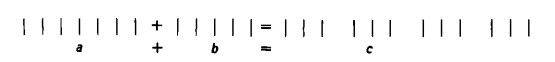
Ora, prendiamo per primo il numero che sta sulla destra, poi quello che sta sulla sinistra, sì da far corrispondere i singoli segni numerici dell’uno e dell’altro. Per visualizzare graficamente ciò, scriviamo:

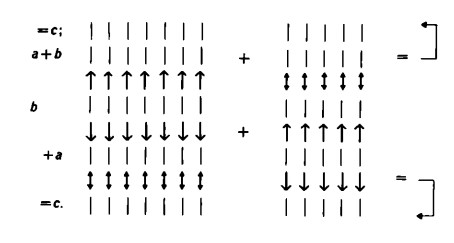
Siccome nell’addizione eseguita in senso inverso si usano gli stessi segni numerici, b + a avrà lo stesso risultato di a + b, cioè c.
Le doppie frecce stanno ad indicare la corrispondenza biunivoca esistente fra i trattini situati nella metà inferiore del disegno con quelli situati nella metà superiore dello stesso; che tali trattini si trovino, poi, in corrispondenza biunivoca tra di loro, non significa altro che essi sono i medesimi, sia che l’operazione venga eseguita in un senso sia in quello inverso.
Se avessimo dei fiammiferi anziché dei trattini stampati, potremmo dimostrare la cosa nella maniera seguente: dopo aver formato la figura

spostiamola verso il basso in modo da far scorrere prima il gruppo di destra  e poi quello di sinistra:

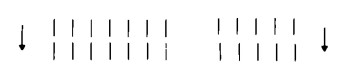
Come si può vedere, non abbiamo fatto nient’altro che riordinare quel dato insieme di fiammiferi un po’ più sotto.
Ciò è ancora più evidente se ci rifacciamo all’esempio del cameriere e dei sottobicchieri. Il cameriere ha a disposizione due sottobicchieri coi quali può calcolare il numero complessivo delle birre consumate

Ora, per calcolare il numero delle birre consumate, può seguire due strade: può controllare prima il sottobicchiere di sinistra e poi quello di destra

o, al contrario, prima il sottobicchiere di destra e poi quello di sinistra

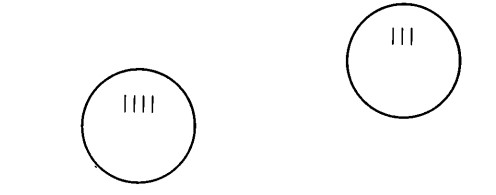
Che il numero complessivo dei segmenti debba rimanere uguale risulta evidente, in questo caso, dal fatto che il cameriere ha avuto a che fare non con singoli trattini, ma con `pacchetti’ di trattini: il numero dei trattini segnato su ognuno dei bicchieri non muta per il fatto che il cameriere inverte l’ordine con cui esegue il calcolo.
Per mostrare la commutatività dell’addizione, abbiamo analizzato degli esempi in cui veniva invertito l’ordine in cui doveva essere eseguita l’addizione dei numeri in questione, ma all’interno delle cifre che rappresentano tali numeri nulla è stato toccato: in esse, cioè, i singoli segni numerici si sono sempre considerati disposti da sinistra verso destra e tale disposizione non è stata mai sottoposta a cambiamenti.
Ora tuttavia possiamo – e per molti aspetti ciò si rivela molto utile da un punto di vista pratico – introdurre accanto all’operazione consistente nell’aggiungere (sulla carta o altrove) segni numerici, l’operazione contraria, consistente invece nel toglierli.

Nell’eventualità di segni scritti, aggiungere segni vorrebbe dire scriverli, mentre il toglierne coinciderebbe col cancellarli o depennarli. Nel primo caso si ha:

Per controllare l’uguaglianza di due numeri abbiamo in precedenza adottato il seguente metodo:

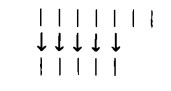
Adesso, col metodo di cancellazione, possiamo procedere anche così:

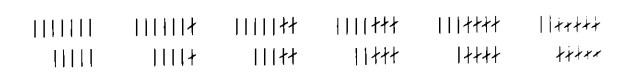
Disponiamo due numeri in maniera tale da poterli confrontare; depenniamo poi un trattino per volta nelle cifre che li rappresentano, contemporaneamente nella cifra superiore e in quella inferiore. Allora, se tutti i trattini di ciascuna cifra vengono cancellati nello stesso momento, numeri sono uguali; se, al contrario, una cifra scompare e rimangono dei raffini appartenenti all’altra, il numero rappresentato da quest’ultima cifra maggiore.
Col metodo della cancellazione la commutatività dell’addizione si può dimostrare in maniera ancora più semplice. Sia, ad esempio da svolgere addizione
Come al solito, l’ordine in cui procederemo è da sinistra verso destra:

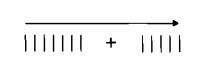
Cancelliamo, ora, seguendo l’ordine esattamente inverso, ossia da destra verso sinistra, ciascun trattino (se i segni numerici fossero fiammiferi anziché trattini stampati, dovremmo dire: `togliamo i fiammiferi’):

Invertendo la direzione del procedimento, abbiamo invertito, in primo luogo, l’ordine in cui si susseguono i numeri da sommare e, secondariamente, l’ordine all’interno di ogni singolo numero, l’ordine, cioè, di successione dei singoli segni numerici. Siccome, però, abbiamo a che fare sempre on gli stessi segni numerici, il risultato dell’addizione deve essere lo stesso. Il procedimento adottato non è privo di fondamento. Infatti, esso vale ton solo per piccoli numeri, come quelli usati nella precedente dimostrazione per motivi di carattere pratico, ma vale anche per numeri grandi a piacere, dal momento che pure in questi casi si ha a che fare con trattini già utilizzati per costruire le cifre. Mediante il metodo della corrispondenza quello della cancellazione è possibile dimostrare la commutatività dell’addizione per tutte le combinazioni numeriche possibili in generale. Si ha dunque

a+b = b + a = c.

Anche a questo punto si può sollevare l’obiezione: la dimostrazione della commutatività non è una dimostrazione rigorosamente matematica, n quanto si limita ad esibire la corrispondenza tra segni numerici; è solo un’illustrazione intuitiva, una `visualizzazione’. E di nuovo sarebbe da rispondere: la nostra dimostrazione della commutatività fondata sulla manipolazione di segni numerici è ‘scientifica’ o ‘non scientifica’ nella misura in cui si può dichiarare ‘scientifico’ o rispettivamente ‘non scientifico’ il programma di costruire in generale tutta la matematica a partire da segni numerici. Se in linea di principio ci è concesso di costruire i numeri come figure costituite da trattini, allora non ci si può negare di impiegare con coerenza queste figure in tutte le dimostrazioni che ci capita di eseguire. E viceversa: chi contesta il valore della nostra dimostrazione della commutatività non può conseguentemente introdurre il concetto di numero come successione di trattini. Un determinato principio deve infatti o valere del tutto o non valere affatto: non può essere giudicato sufficientemente potente in questioni elementari e poi insufficiente in un caso, pur sempre elementare, come la commutatività.

Associatività

L’addizione di tre o più numeri gode di un’ulteriore proprietà, l’associatività Che l’addizione sia associativa significa che il risultato dell’addizione degli stessi numeri associati in maniera diversa è sempre lo stesso. In altri termini: per sommare i tre numeri a, b e c possiamo sommare prima a e b e poi aggiungervi c, oppure sommare b e c e poi aggiungervi a, oppure sommare a e ce poi aggiungervi b. Il risultato è uguale in tutti i casi:

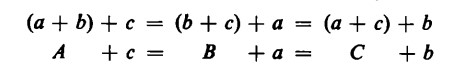
La dimostrazione dell’associatività si ottiene in base allo stesso principio impiegato per dimostrare la proprietà commutativa: in ogni caso i segni numerici usati nella dimostrazione rimangono sempre gli stessi. Di conseguenza, il risultato finale non dipende da come vengono raggruppati tali segni numerici nelle fasi intermedie dell’addizione:

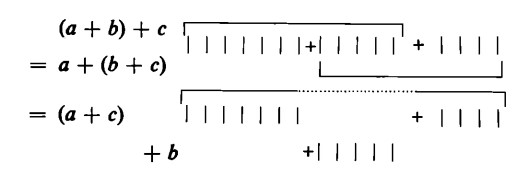
Osserviamo, a questo punto, che in un’addizione i numeri che vengono sommati fra loro si dicono anche addenti , mentre il numero che si ottiene come risultato si chiama somma.

Univocità destra

La legge dell’associatività ci porta ad un’ulteriore proprietà, che dobbiamo dimostrare tuttavia solo in riferimento a due numeri.
Se sommiamo due numeri a e b, il risultato di tale operazione è un numero univocamente determinato c. Ciò significa: il risultato dell’addizione di a e b non può mai essere diverso da c. La ragione di questo fatto è la seguente: quando contiamo dei segni numerici messi in corrispondenza biunivoca, l’ultimo segno numerico contato, ossia quello a cui giungiamo alla fine dell’enumerazione, deve trovarsi contraddistinto dallo stesso numerale:

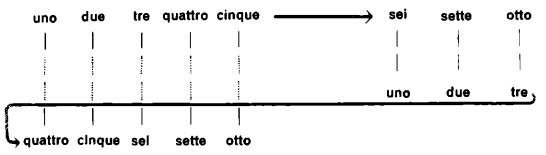
Non vale però il contrario. Cioè: un determinato numero c può essere il risultato dell’addizione di molti altri numeri diversi da a e da b; inoltre il numero c può essere ottenuto persino mediante operazioni su tre o quattro numeri. Ciò trova la sua ragione nel fatto che una cifra costituita da segni numerici, che rappresenta un certo numero, può essere scomposta in cifre rappresentanti numeri minori

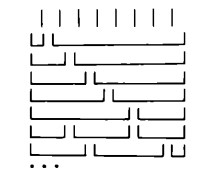
Ogni numero è pensabile come la somma di diverse combinazioni di numeri. D’altra parte, si ha che il numero delle combinazioni possibili cresce con il crescere del numero stesso: il due è scomponibile in uno e uno; il tre è scomponibile in due e uno, e in uno, uno e uno; il quattro è scomponibile in tre e uno, in due e due, in due, uno e uno, e in uno, uno, uno e uno (le permutazioni non sono calcolate); è evidente che le possibilità aumentano con il crescere dei numeri

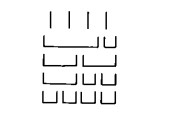
Si ha, quindi, in generale: l’addizione dei numeri a e b dà come risultato sempre e soltanto il numero c; viceversa, il numero c non ‘rimanda’ ai soli numeri a e b, ma può essere scomposto anche in altri numeri. Infatti esso può essere anche il risultato dell’addizione di d e e, nonché di f, g e h, e così di seguito.
Diciamo perciò che l’espressione
a + b = c
è ‘univocamente determinata a destra’. Ciò significa che la somma dei numeri a e b che sta sulla destra è sempre univocamente individuata dal numero c, mentre il numero c non è mai determinato esclusivamente da a e b, ma può essere il risultato dell’addizione di altri numeri:

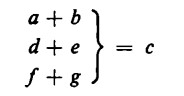
Univocità destrasignifica dunque: a destra sta sempre e soltanto un unico numero, la somma, mentre a sinistra possono comparire diverse combinazioni di addendi.