I segni numerici si ottengono facendo corrispondere a ogni oggetto da contare un’unità (trattino, sassolino o altro):
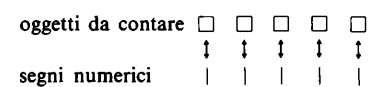
I segni numerici vengono associati in modo univoco agli oggetti da contare. Pertanto si può prescindere dalla natura specifica di quegli oggetti e applicarci soltanto ai segni numerici stessi. Mediante l’operazione del contare si ottengono, dunque, sequenze di trattini di lunghezza diversa:

Fin qui abbiamo associato segni numerici a oggetti, allo scopo di determinare il numero di questi ultimi, siano essi bicchieri di birra o pecore. Ora, però, può accadere di dover confrontare dei numeri tra di loro; così, per esempio, se si vuole trovare quale dei due avventori è il miglior bevitore o chi dei due pastori ha il gregge più numeroso. Naturalmente un tale confronto può sempre essere fatto tra oggetti, proprio come sopra avevamo fatto il confronto tra le mele e le persone di un gruppo; basta disporre in maniera opportuna bicchiere contro bicchiere o pecora contro pecora.
È evidente che ciò sarebbe molto complicato. Dal momento, però, che i nostri segni numerici rappresentano proprio gli oggetti contati, possiamo semplificare notevolmente le cose, disponendo i singoli segni numerici di due figure direttamente l’uno contro l’altro
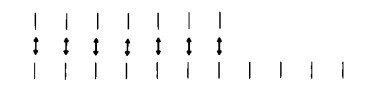
In tal caso non mettiamo in corrispondenza fra loro oggetti e segni numerici, ma solo segni numerici (come precedentemente abbiamo messo in corrispondenza persone e mele, oppure come potremmo mettere in corrispondenza sedie e coperti, coppe e sottocoppe, ecc.). Nel nostro disegno si può facilmente notare che alcuni trattini appartenenti alla serie inferiore rimangono da soli e non vengono posti in corrispondenza con altri della serie superiore (concetto questo che di nuovo ricaviamo dall’esperienza concreta). In altri termini, i segni numerici non si possono ordinare biunivocamente senza resto. Ambedue le figure non sono dunque ‘lunghe uguali’. Le seguenti figure numeriche sono invece ‘lunghe uguali’:
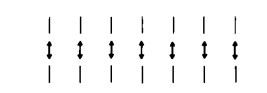
Il significato della parola ‘uguale’, che entra nell’espressione lungo” uguale’, si può cogliere in maniera immediata in forza del significato che assume nella vita di tutti i giorni. Di due figure che non sono lunghe uguali definiamo quella in cui qualche segno numerico rimane isolato (espressione questa con significato univoco nel mondo della prassi) come la ‘più lunga’, l’altra come la ‘più corta’.
A questo punto è necessario precisare (e di ciò si deve essere assolutamente convinti) che nel corso di tutte queste riflessioni non ha alcuna importanza la struttura visiva della figura numerica, ma solo l’idea pratica che essa rappresenta: invece di mettere in corrispondenza due trattini disposti uno sull’altro per mezzo di una freccia, potremo prendere, ad esempio, dei sassolini, metterne contemporaneamente, ma senza preoccupazione di ordine, uno nella mano destra e l’altro nella sinistra, e così di seguito.
Inoltre, come già abbiamo visto, non ha importanza la natura dei segni numerici, che possono essere trattini o oggetti qualsiasi, che si spostano facilmente. I singoli segni possono essere addirittura fisicamente diversi; in questo caso è necessario, però, considerarli uguali perlomeno in quanto segni numerici.
Ora, fissando in modo univoco gli oggetti da usare come segni numerici, è possibile stabilire in ogni caso se una determinata figura è una figura numerica, o no. A partire da ciò potremo sempre confrontarne la lunghezza. Ciò risulta chiaramente con figure come
![]()
Lo stesso vale, però, anche per figure costituite da segni numerici diversi (segni diversi della stessa figura o rispetto ad altre figure) come
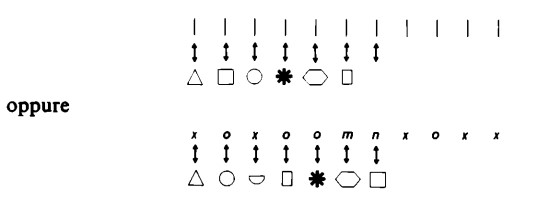
Dal momento, infatti, che tutti questi singoli oggetti o segni grafici sono usati come simboli numerici e si possono quindi associare in modo univoco, è lecito ordinare figure numeriche date secondo la loro ‘lunghezza’. È chiaro che in ambedue gli ultimi esempi le figure che occupano la riga superiore (costituite da trattini nel primo caso e da lettere dell’alfabeto nel secondo) sono più lunghe delle figure inferiori (entrambe costituite da oggetti di forma geometrica).
Al contrario, le figure
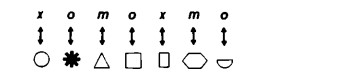
ovvero
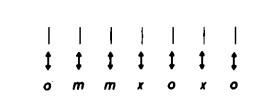
hanno, nonostante la diversità dei loro componenti, pari lunghezza.
Ma che cosa hanno in comune tutte le figure di uguale lunghezza? Evidentemente, ciò che vi ‘rimane’ a prescindere dalla natura specifica dei rispettivi segni numerici, ovvero quanto viene indicato dalle frecce che mettono in corrispondenza. Chiamiamo numero questo alcunché di comune a tutte le figure di pari lunghezza. Diciamo inoltre che ognuna di tali figure costituisce una rappresentazione dello stesso numero.
Di nuovo, il concetto di numero è il risultato di un processo di astrazione; un numero è ciò che viene rappresentato da tutte quelle figure che si possono far corrispondere univocamente segno per segno, a prescindere dal tipo di segni numerici di cui sono costituite. Così, per esempio, ambedue le figure delle ultime due illustrazioni rappresentano lo stesso numero.
A questo punto si mostra necessario fissare una volta per tutte l’uso di alcuni vocaboli, che finora abbiamo usato in modo provvisorio e senza impegno. Il termine ‘figura’ ad esempio, viene usato in matematica per indicare qualsiasi cosa. Finora l’abbiamo utilizzato solo di passaggio, ma proprio l’indeterminatezza era il suo maggior pregio. In seguito non utilizzeremo più la parola ‘figura’, nel senso che le abbiamo conferito sinora; stabiliamo infatti le seguenti norme:
1) chiamiamo segni numerici i singoli oggetti (sassolini, fiammiferi) o i segni grafici (trattini, circoletti, crocette, lettere dell’alfabeto), coi quali formiamo le figure numeriche;
2) chiamiamo cifre le figure numeriche di lunghezza arbitraria, costituite da segni numerici;
3) diciamo inoltre che cifre (ovvero figure numeriche) di pari lunghezza rappresentano lo stesso numero.
La nostra distinzione fra cifra e numero non è quella abituale. Nell’uso linguistico comune, per ‘numero’ si intende quel complesso di segni elementari che designa un numero, ad esempio 374; per ‘cifra’ si intende, al contrario, il singolo segno. Secondo tale distinzione, dunque, il ‘numero’ 374 sarebbe costituito dalle ‘cifre’ 3, 7 e 4. I numeri costituiti da una sola cifra, come per esempio 3, 6 o 8, sarebbero pertanto, allo stesso tempo, cifre e numeri. Secondo invece la terminologia da noi proposta, 374 sarebbe una cifra altrettanto quanto i numeri 3, 7 e 4 singolarmente presi, e il numero 374 si potrebbe altrettanto bene designare con la figura in cifre romane CCCLXXIV o con una serie di trecentosettantaquattro trattini.
Confronto di tre numeri
Finora abbiamo esaminato casi in cui la relazione di uguaglianza o disuguaglianza era attribuita solo a coppie di numeri; ora, invece, vogliamo prendere in considerazione anche casi più complessi, casi cioè in cui sono messi a confronto tre numeri:
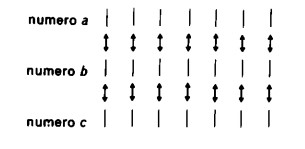
Le frecce di corrispondenza stanno a indicare che il numero a e il numero b sono uguali tra loro e che lo stesso vale per il numero b e il numero c.
È naturale chiedersi a questo punto: il numero a e il numero c sono anch’essi uguali, pur non essendo direttamente collegati da frecce di corrispondenza? Il nostro metodo di ordinamento (fondato sulla pratica quotidiana) ci mostra che le cose stanno effettivamente così. Possiamo infatti associare a ogni segno numerico della fila b un segno di a e, allo stesso tempo, uno di c, disponendo contemporaneamente con le due mani da una parte e dall’altra di una fila di sassolini (o fiammiferi) due nuove file: il significato dell’espressione ‘da una parte e dall’altra’ è nella prassi quotidiana ben chiaro.
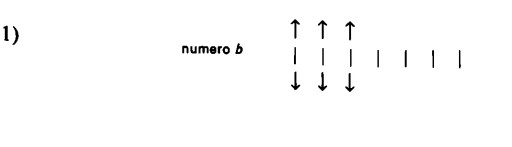
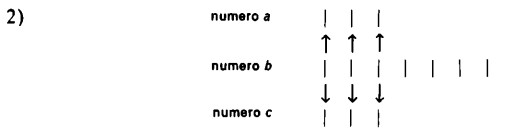
Mettendo in corrispondenza i segni di due nuove file con quelli di una fila già data, si associano nel contempo, evidentemente, anche i segni delle nuove file direttamente tra loro. A questo punto, possiamo lasciar cadere la sequenza intermedia b, ottenendo così le sole due sequenze a e c, poste direttamente in corrispondenza tra loro:
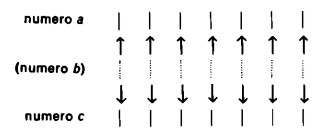
Con ciò abbiamo ottenuto il seguente risultato: se due numeri a e b sono uguali, e lo stesso vale per i numeri b e c, allora sono uguali fra loro anche i numeri a e c, e di ciò si può star sicuri senza confrontarli direttamente.
Qui è da fare attenzione, però, ad una sottile distinzione, della qu finora non abbiamo fatto uso, in sostanza perché non ce n’era bisogno.
Se due numeri a e b risultano uguali, possiamo dire sia che ‘a è uguale a b’, sia che ‘b è uguale ad a’. Ambedue le proposizioni esprimono la medesima cosa, dal momento che l’ordinamento trattino per trattino può essere indifferentemente eseguito in ambedue le direzioni. Se, per esempio costruiamo cifre uguali ponendo contemporaneamente un sassolino a destra e uno a sinistra, è ovviamente indifferente far corrispondere l’attività della mano sinistra all’attività della mano destra o, al contrario, l’attività della destra a quella della sinistra. In ciò consiste la cosiddetta propri commutativa della relazione di uguaglianza.
Se confrontiamo fra loro tre numeri a, b, e c e consideriamo come numero intermedio b, possiamo dire sia:
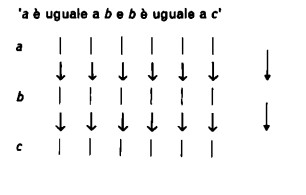
sia, invertendo in parte l’ordine del confronto:
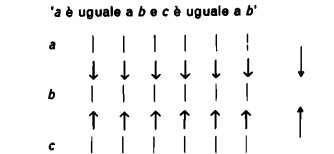
(infatti ‘b è uguale a c’ e ‘c è uguale a b’ sono espressioni interscambiabili). Se ora ritorniamo al risultato sopra dimostrato ‘a è uguale a c’, otteniamo le seguenti due figure distinte:
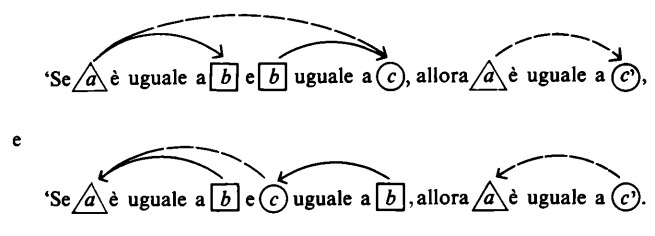
Nella prima proposizione passiamo da a a b, e poi da b a c; percorriamo dunque, nel processo di ordinamento, il sistema, per così dire, nella stessa direzione:
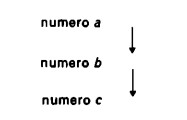
Nella seconda proposizione b occupa lo stesso posto, ma viene confrontato la prima volta con a e poi con c. L’ordinamento avviene così in due diverse direzioni:
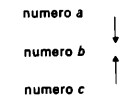
In conformità con quanto detto, per confrontare tre numeri si possono seguire due strade differenti: la strada che ‘passa’ per la posizione intermedia e quella che vi si ‘dirige’ da parti opposte. Chiamiamo la prima via ‘transitiva’ (traffico in transito si dice proprio quel traffico che si muove da un paese a ad un paese c attraverso il paese b, per esempio dalla Scandinavia all’Italia attraverso la Germania); la seconda, cioè quella che partendo dall’esterno conduce al centro, la chiamiamo via ‘comparativa’. Distinguiamo quindi:
1) la `transitività dell’uguaglianza’:
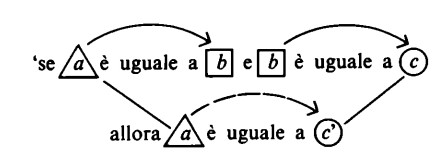
(la transitività è caratterizzata dal fatto che a e c mantengono sempre il loro posto a sinistra o a destra, mentre b muta la sua posizione);
2) la ‘comparatività’ dell’uguaglianza:
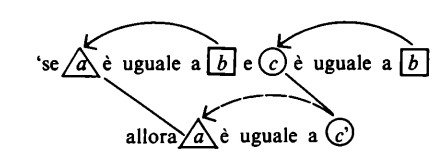
(la comparatività è caratterizzata dal fatto che b resta sempre a destra).
È evidente a questo punto che l’ordine diverso in cui si susseguono le operazioni non muta il significato della conclusione: ‘a si trova in corrispondenza con b’ ha lo stesso significato di `b si trova in corrispondenza con a’
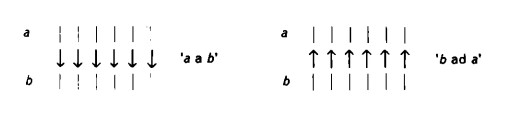
e, rispettivamente, `b si trova in corrispondenza con c’ ha lo stesso significato di ‘e si trova in corrispondenza con b’. In ciò consiste, come sopra abbiamo detto, la commutatività del rapporto di uguaglianza.
Nel caso di tre numeri si ha inoltre che è indifferente mettere in corrispondenza a e b (rispettivamente, b e a) e poi b e c (rispettivamente, c e b) o, viceversa, prima b e c (rispettivamente, c e b) e poi a e b (rispettivamente, b e a).
Perciò, nelle proposizioni finora considerate, possiamo invertire le parti e ottenere, così, altri due enunciati (operando lo scambio intorno all’espressione `uguale’): ‘se b è uguale ad a e c è uguale a b, allora c è uguale ad a’ e ‘se b è uguale ad a e b è uguale a c, allora e è uguale ad a’.
La formulazione di questi due enunciati non è soddisfacente, dal momento che nell’antecedente del condizionale compare prima a e poi c, nel conseguente prima c e poi a. È opportuno, pertanto, scambiare l’antecedente facendo perno sull’espressione ‘e’; otteniamo così:
`se e è uguale a b e b è uguale ad a,
allora c è uguale ad a’,
e
`se b è uguale a e e b è uguale ad a,
allora c è uguale ad a’.
La prima proposizione esprime di nuovo la transitività, però questa volta nel senso inverso, ossia da c ad a passando per b; la seconda esprime, invece, la comparatività: questa volta, però, il membro b sta a sinistra anziché a destra. Chiamiamo, perciò, la prima legge di comparatività, in cui il termine medio b sta sempre a destra, comparatività destra, e la nuova legge, in cui b sta invece a sinistra, comparatività sinistra.
Volendo, potremmo parlare anche di una transitività da sinistra a destra e di una transitività da destra a sinistra; tale distinzione non è tuttavia abituale.
Le riflessioni ora svolte sembrano banali e del tutto superflue. Che l’uguaglianza sia commutativa, transitiva e comparativa, sembra a prima vista ovvio e in effetti lo è. Tuttavia, in matematica esistono numerosi casi in cui non si può scambiare arbitrariamente l’ordine in cui compaiono figure ed espressioni. Per questo motivo, la validità dell’interscambiabilità dei termini deve essere esplicitamente dimostrata caso per caso.
Naturalmente, anche qui, non si deve dare eccessiva importanza al significato letterale delle espressioni ‘sinistra’ o ‘destra’. A tale proposito, dobbiamo ribadire ancora una volta che la visualizzazione delle operazioni matematiche, come tale, è senza importanza. Si tratta piuttosto di far corrispondere, come si fa abitualmente nella pratica quotidiana, segni di una sequenza a segni di un’altra. Lo svolgimento di tali operazioni con segni grafici è soltanto uno dei tanti modi possibili, scelto di comune accordo per ragioni di convenienza. Dal momento che normalmente si scrive da sinistra a destra, segno posto ‘a sinistra’ non significa nient’altro che segno posto ‘prima nel tempo’ e, rispettivamente, segno posto ‘a destra’ significherà segno posto ‘dopo nel tempo’.
Potremmo scrivere altrettanto bene dall’alto verso il basso e parlare, di conseguenza, di comparatività ‘dall’alto verso il basso’ e di comparatività ‘dal basso verso l’alto’. Se poi convenissimo che la direzione della scrittura dovesse andare dal basso a destra verso l’alto a sinistra, potremmo dire, anziché ‘da sinistra’, ‘dal basso a destra’ e, anziché ‘a destra’, ‘verso l’alto a sinistra’.
Dunque, il significato di espressioni come ‘a sinistra’ e ‘a destra’ non può essere rettamente inteso in matematica senza far riferimento ad una determinata guisa di scrittura concordata, la quale d’altra parte deve essere concepita come la traduzione in termini grafici di operazioni pratiche della vita quotidiana.
Scrivere un segno o costruire una figura ‘a sinistra’ o ‘sopra’, serve, dunque, a nient’altro che ad esprimere l’idea temporale del ‘prima’.
Certamente anche qui si può obiettare che locuzioni linguistiche come ‘fare qualcosa’, ‘prima’ e ‘dopo’ riposano sull’intuizione della nozione di tempo, come d’altra parte, le espressioni ‘a sinistra’, ‘a destra’, ‘sopra’, ‘sotto’ riposano sull’intuizione della nozione di spazio. Ma ciò è inevitabile, dal momento che non si può regredire oltre l’esperienza vissuta. Per questo, noi definiamo col termine, caratteristico della pratica quotidiana, di ‘operazione’ i movimenti spazio-temporali che eseguiamo, ad esempio, per disporre dei sassolini su una superficie, senza analizzare ulteriormente il concetto di operazione.
Come abbiamo visto, i numeri sono il risultato di operazioni eseguite con file di trattini. Queste ultime non sono fondamentalmente altro che successioni non articolate di trattini. Simboli per complessi di trattini ci servono solo per comodità. Essi sono solo segni stenografici che non mutano affatto la natura delle cose; in particolare, i numeri rimangono sempre definiti attraverso sequenze di segni svolgenti la funzione di unità numeriche e quindi, in quanto tali, uguali tra di loro.