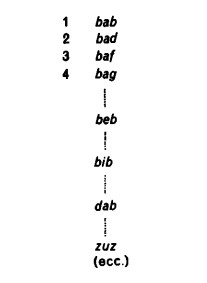
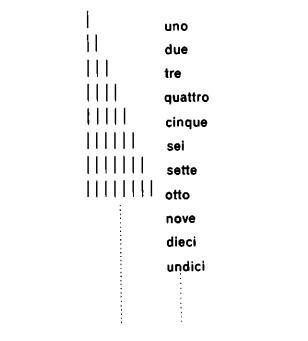
I numeri si costruiscono a partire da successioni di trattini o di altri segni atti a contare. Ci serviamo di tali segni per costruire le figure elementari costituite da un solo trattino, dopodiché, aggiungendo un nuovo trattino a figure già scritte, otteniamo tutte le figure.
Non potremmo tuttavia lavorare con numeri se non usassimo dei nomi per ognuno di essi. Per identificare un determinato numero è necessario associare alla figura che lo rappresenta una parola che lo contraddistingua in maniera univoca, un numerale. Questa necessità di dare un nome ai numeri è da distinguere dalle necessità di raccogliere i numeri in unità più comprensive, come le cinquine, le decine, le dozzine, ecc. Naturalmente i nomi per designare i numeri sono formati di regola in base a schemi di raccoglimento del tipo: tre, tredici, ventitré. Ma questo non è necessario. In teoria si potrebbero usare come numerali sillabe qualsiasi, ottenute combinando le lettere in modo da esaurire ogni caso possibile senza ripetizioni
Per esempio, invece di dire ‘trecentosettantaquattro pecore’, si potrebbe dire altrettanto bene `kup pecore’, ove `kup’ è un numerale non costruito secondo una precisa legge di composizione, ma scelto arbitrariamente.
Contare mediante numerali è utile per la seguente ragione pratica: si impara a memoria una serie di parole scelte in maniera del tutto arbitraria, ma fissate una volta per tutte (anche l’alfabeto si impara in maniera simile), dopodiché si associa ad ogni segno di una determinata figura una di queste parole. Il numerale che si associa all’ultimo segno della serie designa il numero in questione.
Abbiamo visto che i numerali vengono scelti in maniera fondamentalmente arbitraria; ciò è confermato dal fatto che nelle lingue a noi più vicine, quelle indoeuropee, i numeri dall’uno al dieci — corrispondenti al numero delle dita — si designano con parole scelte a caso e senza legami di affinità tra di loro: uno, due, tre, quattro, … Questi nomi si devono semplicemente imparare a memoria in modo da poterli associare meccanicamente agli oggetti da contare. Solo a partire da ‘undici’ (`undecim’ ecc.) i numerali vengono costruiti, in analogia con certi segni numerici, secondo schemi di unificazione determinati, anche se in linea di principio non necessari.
In margine a tali riflessioni, è da osservare che l’introduzione di un numerale per ogni numero rende superfluo l’uso delle successioni di trattini in molte situazioni della vita quotidiana; infatti, servendosi dei numerali e senza ricorrere a successioni di trattini, si possono contare direttamente anche quegli oggetti che non sono dei segni numerici come, per esempio, le pecore. Come si sa; questo non è, però, sempre il procedimento più pratico; il cameriere traccia i suoi segni sul sottobicchiere, proprio perché altrimenti non potrebbe ricordarsi il numerale corrispondente al numero dei bicchieri bevuti; chi poi volesse, per esempio, contare le automobili che transitano su un ponte o su un’autostrada, senza dubbio riuscirà a contarle molto più facilmente tracciando una sequenza di trattini che non servendosi di numerali, con i quali molto probabilmente ‘perderebbe la testa’.
Associamo, comunque, un numerale ad ogni figura costituita da segni numerici, cioè ad ogni cifra, giacché in ogni caso dobbiamo dare un nome al ‘risultato finale’ della computazione.