In questa guida spieghiamo come si fanno le operazioni con le frazioni.
Operazioni con le Frazioni
Come è possibile operare con numeri frazionari?
Le leggi che regolano il calcolo con frazioni sono un capitolo notoriamente difficile della matematica. Per rendere più comprensibile l’esposizione, incominciamo con alcuni esempi numerici; tali esempi, tuttavia, pur rappresentando un valido sostegno intuitivo per l’argomentazione rigorosa, non possono essere considerati come sostitutivi.
Potremmo illustrare ogni passaggio con le nostre figure di trattini; tuttavia in questa occasione facciamo a meno di tali rappresentazioni, dal momento che si raggiungono i medesimi risultati, e spesso con maggior rapidità e chiarezza, anche se ci si serve esclusivamente di esemplificazioni numeriche.
Problemi come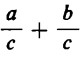 
ci sono già familiari; ne abbiamo, infatti, parlato a proposito della proprietà distributiva della divisione rispetto alla somma; ora, si ha che
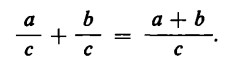
Il corrispondente vale per la sottrazione:
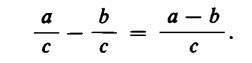
Ciò, in pratica, significa che la somma, o differenza, di due frazioni aventi lo stesso denominatore si ottiene sommando, o sottraendo, i numeratori e lasciando invariato il denominatore.
Ma che fare quando i denominatori sono diversi?
Come facciamo, in altri termini, a sommare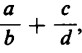 
ad esempio 
?
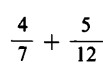Oppure, come si moltiplicano e si dividono i numeri frazionari?
Per trovare una soluzione a tali problemi, dobbiamo fare un passo indietro e riprendere un’idea, che abbiamo discusso brevemente nelle pagine precedenti.
Abbiamo visto sopra che ogni numero intero si può scrivere come differenza di infinite coppie di numeri interi diversi. Così + 4 si può scrivere anche come 5 – 1, 6 – 2, 7 – 3 e così via, oppure, prendendo in considerazione anche i numeri negativi, come 4 – 0, 3 – (- 1) = 3 + 1, 2 – ( – 2) = 2 + 2, 1 – (- 3) = 1 + 3, 0 – (- 4) = -1 + 5, ecc.
Queste considerazioni si possono estendere dall’ambito dell’addizione o i sottrazione a quello della moltiplicazione e divisione. In tal caso, al numero intero corrisponde il numero frazionario, e alla differenza (come risultato della sottrazione) corrisponde il quoziente (come risultato della divisione).
Deriva da questo fatto che ogni numero frazionario può essere inteso come quoziente di un numero infinito di coppie di numeri distinti. Vediamo ora di chiarire questo concetto.
Si consideri, ad esempio, il seguente schema:
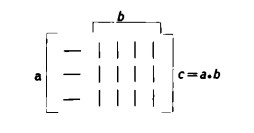
Sappiamo che l’intero schema di trattini rappresenta il dividendo c. Sappiamo inoltre che l’operazione del dividere consiste nel ridurre tale schema ad una sola riga, ovvero colonna.
Se abbiamo a righe e b colonne, eseguire la divisione 
significa ridurre l’intero schema a una sola riga, eseguire la divisione
, invece, ridurlo a una sola colonna.
Allunghiamo ora le nostre righe, aumentiamo cioè del doppio il totale delle colonne
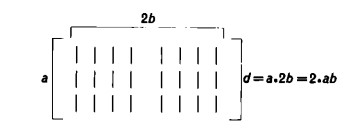
Ovviamente il totale dei trattini sarà raddoppiato.
Tuttavia, se lo dividiamo per il nuovo numero di colonne 2b allo scopo di ridurlo a una sola colonna, otterremo l’originario numero di righe a; infatti, nonostante la trasformazione dello schema di partenza, il numero delle righe è rimasto invariato.
Se avessimo allungato le colonne anziché le righe e avessimo pertanto aumentato il numero delle righe, avremmo ottenuto, naturalmente, il risultato corrispondente
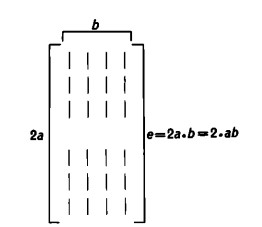
Di conseguenza: se dividiamo il doppio di un numero per il doppio del divisore, il risultato resta lo stesso.
Si può dimostrare che lo stesso vale anche nel caso in cui si dimezza numero dei trattini dello schema:
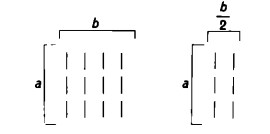
Se si divide lo schema di trattini cosi dimezzato per la metà del numero elle colonne, si ottiene sempre lo stesso numero di righe e, analogamente, scambiando le righe con le colonne.
Quanto si è visto per il raddoppio e il dimezzamento vale anche per la moltiplicazione e divisione per un numero naturale qualsiasi.
Ad esempio, se a 2, 3, 4, 5 volte un certo numero di bambini devono ;sere distribuite 2, 3, 4, 5 volte un certo numero di mele, ogni bambino ottiene sempre lo stesso numero di mele. Il maggior numero di mele eguaglia, per così dire, il maggior numero di bambini:
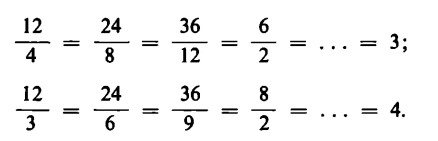
Ma si ha anche:
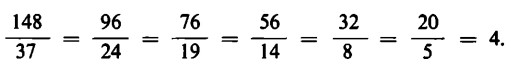
In altre parole: frazioni che si ottengono l’una dall’altra moltiplicando per lo stesso numero numeratore e denominatore, rappresentano lo stesso numero frazionario.
Parliamo di ‘ampliare’ o ‘semplificare’ una frazione quando moltiplichiamo o, rispettivamente, dividiamo per lo stesso numero il numeratore e il denominatore della frazione stessa.
Ovviamente si possono ampliare o semplificare anche quelle frazioni che, calcolate, non danno come risultato un numero intero. Frazioni come
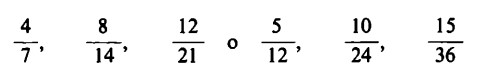
hanno lo stesso valore. Ciò appare chiaro dalla seguente considerazione.
Si abbiano 4 mele da distribuire tra 7 bambini. Si aggiungano altre 4 mele, ma contemporaneamente aumenti di 7 anche il numero dei bambini. Siccome alla seconda distribuzione sono interessati altrettanti bambini e mele quanti nella prima, il secondo gruppo di bambini otterrà lo stesso numero di mele del primo.
Un numero frazionario rimane pertanto invariato se numeratore e denominatore vengono moltiplicati o divisi per lo stesso numero:
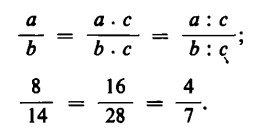
A scuola si è soliti dire: `frazioni’ diverse possono avere lo stesso ‘valore’
Noi preferiamo evitare, tuttavia, l’espressione ‘valore’ e dire semplicemente ‘numero’.
Come il numero 4 può essere espresso attraverso le coppie numeriche
5 – 1, 6 – 2, 7 – 3, 8 – 4, 9 – 5, oppure il numero 5 attraverso le coppie numeriche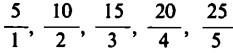 
, così anche numero 
può esprimere mediante le seguenti coppie numeriche:
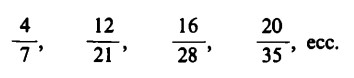
Chiamiamo semplicemente. ‘numero frazionario’ ciò che normalmente viene chiamato ‘valore di una frazione’; inoltre chiamiamo semplicemente ‘coppia di numeri’ ciò che normalmente viene chiamato ‘frazione’, cioè un’espressione con un determinato numeratore e un determinato denominatore.
Qui, ovviamente, adottiamo un tipico procedimento di astrazione, in quanto diciamo: tutte le coppie numeriche che si ottengono scrivendo un numero sotto ed uno sopra il segno fratto e che sono sostituibili una all’altra, rappresentano lo stesso numero frazionario.
Addizione e Sottrazione con Frazioni
Mentre nell’ambito dei numeri interi la possibilità di esprimere lo stesso numero attraverso infinite coppie diverse di numeri poteva sembrare un puro gioco, senza vero interesse scientifico, nel calcolo delle frazioni si rivela uno strumento di essenziale utilità. Infatti, sfruttando il concetto di uguaglianza tra numeri frazionari, possiamo eseguire la somma e la sottrazione anche con frazioni.
Vediamo un semplice esempio. Come facciamo a calcolare la somma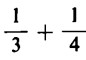 
?
Trasformiamo ambedue le frazioni in modo che i denominatori delle stesse vengano a coincidere con lo stesso numero, in questo caso con 12. Ne risulta:
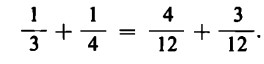
Possiamo, allora, calcolare il valore della somma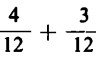 
esso è 
.
In maniera del tutto analoga si ha:
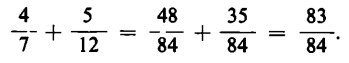
Gli esempi appena illustrati ci mostrano qual è il procedimento da intraprendere: cerchiamo innanzitutto il ‘denominatore comune’, in modo da poter trasformare ambedue le frazioni in frazioni aventi lo stesso denominatore. Il denominatore comune è ‘nel caso più sfavorevole’ il prodotto di ambedue i denominatori di partenza, dal momento che questo è in ogni caso un multiplo di ambedue i denominatori. Nel primo caso, il denominatore comune era 12. Per arrivare a 12, dobbiamo moltiplicare il 4 per 3 e il 3 per 4. Il numero per il quale si deve moltiplicare le frazioni è dunque per ogni frazione il denominatore dell’altra. (Se i numeri, poi, sono `imparentati in maniera più stretta’, il ‘minimo comune multiplo’ è un numero più piccolo rispetto al prodotto dei denominatori; il calcolo in questo caso risulta più semplice. Per esempio, se i denominatori sono 8 e 12, il minimo comune denominatore è 24. Comunque a questo punto ciò non ci interessa, dal momento che, utilizzando numeri generici, non si possono esplicitare senz’altro tali ‘parentele’ fra i numeri.)
In numeri generici, si avranno così da sommare le frazioni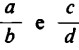 
Innanzitutto occorre cercare il denominatore comune. Come denominatore comune possiamo considerare il prodotto dei denominatori:
bd.
Dopodiché occorre ‘ampliare’ ognuna delle due frazioni, seguendo il metodo seguente: si moltiplica il numeratore di ognuna di esse per quel fattore per il quale è stato moltiplicato il denominatore corrispondente a
allo scopo di ottenere il denominatore comune, vale a dire 
per d e 
per b.
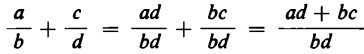
In parole: la somma di due frazioni non è altro che una frazione il cui numeratore è la somma dei prodotti ottenuti ‘moltiplicando in croce’ i numeri costituenti le frazioni di partenza e per denominatore il prodotto di ambedue i denominatori.
Un risultato parallelo vale anche nel caso della sottrazione di frazioni.
Moltiplicazione e Divisione con Frazioni
Frazioni e numeri interi
a) Moltiplicazione tra frazioni e numeri interi.
Che cosa si debba intendere per moltiplicazione di una frazione per un numero intero, lo si può capire dalla semplice riflessione che segue.
Ogni frazione rappresenta in realtà un numero; la moltiplicazione di una frazione per un numero intero si riduce, di conseguenza, alla moltiplicazione del numero che è rappresentato mediante quella frazione per il numero intero in questione.
Il caso più semplice è quello di una frazione nella quale il numeratore è divisibile per il denominatore. Se abbiamo dodici mele da distribuire a quattro bambini, ogni bambino riceve tre mele.
3 è, dunque, il numero `rappresentato’ dalla frazione 
. Ora sí moltiplichi il numero 3, per esempio, per 2; si ottiene il risultato 6. Siccome il numero frazionario rappresenta il numero delle mele che tocca a ciascun bambino, il problema è: quante mele dobbiamo avere per dare allo stesso gruppo di bambini un numero doppio di mele ciascuno? La risposta è: anziché 12 mele, ce ne occorrono 24. che verranno distribuite ai 4 bambini, in modo che a ciascuno ne tocchino esattamente 6. Si ha quindi:
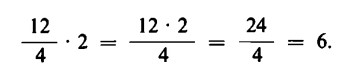
Per moltiplicare una frazione per un numero intero, basta moltiplicare per quel numero il numeratore e lasciare invariato il denominatore. Questa legge vale anche nel caso in cui il numero rappresentato dalla frazione non è un numero intero.
Prendiamo per ragioni di semplicità una frazione `propria’, in cui il numeratore è minore del denominatore.
Se 4 mele sono da distribuire tra 7 bambini, ogni bambino riceve 
di mela. Il senso intuitivo di questa frazione è il seguente: ogni mela è stata divisa in 7 parti e ad ogni bambino è toccato un settimo di ogni mela.
La moltiplicazione della frazione per 2, 3, 4, … ha evidentemente il seguente significato intuitivo: ad ogni bambino spetta due volte, tre volte, quattro volte, .. . `un settimo’ di mela. Prendiamo dunque 8, 12, 16 .. . mele invece di 4; suddividiamole nel modo descritto una dopo l’altra in sette parti uguali e distribuiamole ai ragazzi: ogni ragazzo riceverà 8/7, 12/7, 16/7 ….. ‘di mela’.
Le riflessioni ora svolte ci mostrano che una frazione si moltiplica per un numero intero, moltiplicando per questo numero il numeratore della frazione stessa:
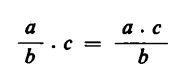
Questa operazione è assai importante ai fini pratici del calcolo, dal momento che ci permette di collocare le parti del numeratore di una frazione o i fattori ad esso uniti indifferentemente sopra il segno fratto o accanto ad esso:
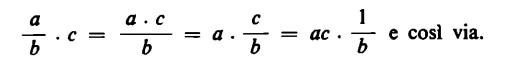
In seguito, poi, alla commutatività della moltiplicazione, vale lo stesso anche nel caso in cui la frazione si trova al secondo posto.
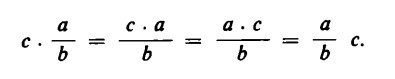
Approfondiamo ulteriormente questo caso, per meglio intendere la moltiplicazione di due frazioni. Ritorniamo al nostro esempio delle mele.
Supponiamo di avere due bambini. A ciascuno vogliamo dare tante mele quante toccherebbero a ciascun bambino, se ci fossero 12 mele da dividere tra 4 bambini. In totale:
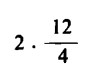
Possiamo risolvere il problema in due modi differenti. Possiamo semplificare la frazione e ottenere così:
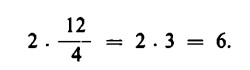
Possiamo partire, altrimenti, dalla seguente riflessione:
Se a ciascuno dei 2 bambini toccassero 12 mele, avremmo bisogno di 2 per 12 = 24 mele. Ai bambini, però, non spettano 24 mele, ma soltanto la parte di un quantitativo (arbitrario) di mele che dovrebbe toccare a quattro bambini, cioè un quarto. Facendo i calcoli, si ha:
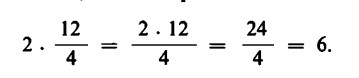
Ora, poiché non è possibile calcolare prima una frazione che non dà un numero intero, di solito rimane l’altra soluzione, che segue.
Per moltiplicare un numero intero per una frazione, si moltiplica prima quel numero per il numeratore e si divide poi il risultato per il denominatore. Ad esempio:
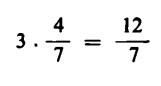
Tale risultato si può derivare immediatamente anche dalla legge, sopra enunciata, della moltiplicazione di una frazione per un numero intero, dal momento che la moltiplicazione è commutativa:
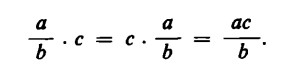
b) Divisione di una frazione per un numero intero. Prima di affrontare il caso della moltiplicazione di due frazioni, vogliamo chiarire qual è il significato della divisione di una frazione per un numero intero, o viceversa.
Supponiamo di dover dividere la frazione 
per 2. Che cosa significa questo?
è la parte di mele che tocca a 3 bambini se le mele da distribuire sono 12.
Ora, questa parte deve essere ulteriormente divisa per due; ogni bambino riceve, dunque, la metà di quanto avrebbe ricevuto prima.
La riduzione a metà della parte che tocca a ciascuno può essere spiegata in due diverse maniere. O la quantità complessiva di mele è stata ridotta della metà, di modo che la quantità di mele da distribuire ai bambini risulta minore, oppure i bambini sono diventati il doppio, di modo che la stessa quantità di mele deve essere suddivisa tra un numero doppio di bambini.
L’espressione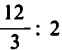 
si può dunque leggere come
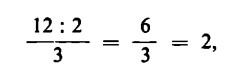
(ai tre bambini si può distribuire solo metà della quantità originaria di mele),
oppure come
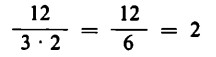
(la stessa quantità di mele si deve suddividere tra un numero doppio di bambini).
Pertanto, per dividere una frazione per un numero intero, basta dividere per quel numero il numeratore (ci sono allora meno mele), oppure moltiplicare per lo stesso numero il denominatore (ci sono allora più bambini).
Ci sono dei casi in cui la divisione del numeratore non si può eseguire; la moltiplicazione del denominatore, al contrario, si può sempre eseguire. Si avrà così:
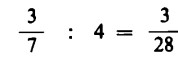
che significa: tre mele, che, in un primo momento, si dovevano suddividere
tra 7 bambini, ora si devono suddividere tra 28.
Con numeri generici si ha:
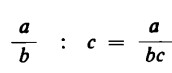
Analoghe considerazioni si possono fare anche nel caso della divisione di un numero intero per una frazione.
Supponiamo di avere 24 mele e di doverle distribuire tra 12 bambini.
A ogni bambino toccheranno, di conseguenza, solo 2 mele: 
.
Supponiamo, però, che il loro numero si riduca: i dodici bambini si dividono in tre gruppi uguali e due di tali gruppi se ne vanno a giocare; dovremo allora distribuire le 24 mele a quelli rimasti, il cui numero si è ridotto di un fattore 3. L’operazione da risolvere sarà quindi:
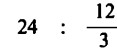
Anche qui possiamo calcolare prima il valore della frazione. Noi sappiamo che, se dividiamo il gruppo di 12 bambini in tre sottogruppi uguali, ogni sottogruppo risulta composto di 4 bambini:
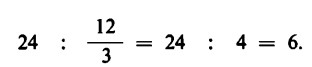
È possibile, però, procedere anche in questo modo: distribuire una data quantità di mele a un terzo dei bambini presenti all’inizio è come distribuire quella quantità di mele triplicata al numero di bambini presenti all’inizio. Eseguiremo quindi il nostro calcolo operando senz’altro sul quantitativo di mele triplicato e sul numero invariato di bambini:
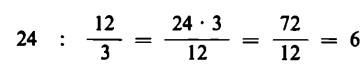
Se esprimiamo il risultato ora ottenuto con numeri generici, si ha la relazione:
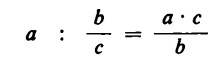
Pertanto, la divisione di un numero per una frazione si esegue moltiplicando quel numero per il denominatore e dividendo il risultato per il numeratore.
Due frazioni
Giunti a questo punto, siamo in grado di eseguire moltiplicazioni e divisioni con due frazioni.
Naturalmente potremmo partire anche qui dall’esempio delle mele e dei bambini. Tuttavia, già gli esempi per le operazioni fra numeri interi e frazioni ci hanno mostrato quanto facilmente si raggiunga il limite oltre il quale gli esempi diventano troppo complicati e perciò artificiosi.
Nel caso di operazioni tra numeri interi e frazioni, l’introduzione di esempi numerici con mele e bambini era, da una parte, utile per la comprensione, dall’altra, non richiedeva un grado troppo alto di artificiosità.
Per operazioni con due frazioni, al contrario, non abbiamo più bisogno di esempi numerici, poiché lavoreremo solo su trasformazioni di formule già dimostrate né, d’altra parte, gli esempi riuscirebbero convenienti.
a) Moltiplicazione di due frazioni. La moltiplicazione di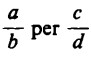 
si può considerare scomposta in due operazioni successive, in ciascuna delle quali si ha a che fare solo con un numero intero e una frazione.
Prima si moltiplica 
per il numero intero c e si divide poi il risultato ottenuto, che è a sua volta una frazione, per il numero intero d.
Moltiplicando il numeratore a per il numero intero c, otteniamo 
Dopodiché, moltiplicando il denominatore b per d, dividiamo la frazione cosi ottenuta per d. Riassumendo i passaggi, otteniamo:
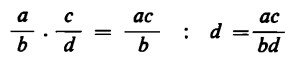
Per moltiplicare, dunque, due frazioni, basta moltiplicare il numeratore dell’una per il numeratore dell’altra e, viceversa, il denominatore dell’una per il denominatore dell’altra.
b) Divisione di due frazioni. È possibile calcolare con un procedimento del tutto analogo anche il caso della divisione di due frazioni:
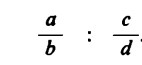
Anche questa operazione si può scomporre in due momenti successivi.
Dividiamo anzitutto la frazione 
per il numero intero c, moltiplicando il denominatore b per il numero intero c:
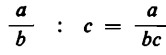
Ma noi sappiamo già come si esegue la divisione di un numero intero per una frazione:
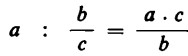
Possiamo pertanto indicare con A il numero frazionario corrispondente al dividendo e calcolare:
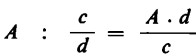
A questo punto, introduciamo di nuovo al posto di A; otteniamo così una ‘frazione in una frazione’:
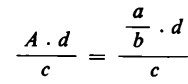
Trasformiamo il numeratore della frazione
Scriviamo ora al posto di
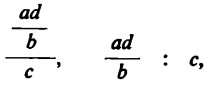
il che, come sappiamo, dà come risultato 
. Con ciò è dimostrato che
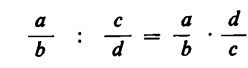
Si ottiene il medesimo risultato ponendo, anziché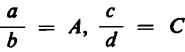 
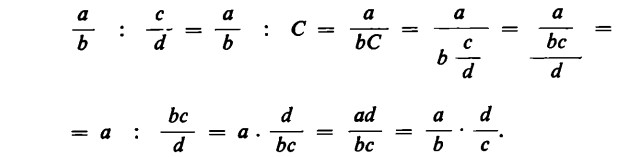
In conclusione, per dividere una frazione per un’altra, basta moltiplicare la prima frazione per l’inverso dell’altra.