Se sommiamo o moltiplichiamo due numeri naturali, otteniamo sicuramente un numero naturale. Se, al contrario, sottraiamo o dividiamo due numeri naturali, non sempre otteniamo un numero naturale. Quindi, se vogliamo eseguire in ogni caso la sottrazione e la divisione, dobbiamo costruire due nuovi domini numerici, quello dei numeri negativi e quello dei numeri frazionari. Per poter poi sempre eseguire l’operazione di estrazione di radice e quella di logaritmo, dobbiamo creare il dominio dei numeri reali.
Nel calcolo con i numeri viene perciò sempre a galla il problema della `società chiusa’: rimaniamo sempre noi soli o entrano nuovi ospiti?
In base a tale punto di vista, che considera la delimitazione di insiemi numerici in riferimento all’eseguibilità delle operazioni, i matematici hanno definito negli ultimi decenni determinate entità, che noi designamo col termine generico di ‘strutture numeriche’.
Prendiamo, ad esempio, il dominio dei numeri naturali. Da che cosa è caratterizzato tale dominio?
Ogni addizione e ogni moltiplicazione di due numeri naturali dà come risultato un nuovo numero naturale, al contrario ciò non vale per ogni sottrazione e per ogni divisione.
Addizione e moltiplicazione sono operazioni associative e commutative.
La moltiplicazione, a sua volta, è distributiva rispetto all’addizione, ma non viceversa.
Nella moltiplicazione (e divisione) esiste un ‘elemento neutro’, cioè un numero che moltiplicato per un altro lascia quest’ultimo invariato. Questo numero è 1. Infatti ogni numero rimane invariato, se è moltiplicato per 1: a 1 = a (e anche: 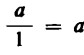 ).
).
Nell’addizione non esiste un simile elemento neutro; infatti, l’addizione di I con un numero porta al successore di quest’ultimo. Se invece si considera anche lo zero come numero naturale, si ha un elemento neutro anche per l’addizione; infatti, l’addizione di zero lascia invariato ogni numero: a + 0 = a.
Allarghiamo ora il dominio dei numeri naturali al dominio dei numeri interi aggiungendo ai primi l’insieme dei numeri negativi. Quali possibilità si danno a questo punto?
La sottrazione si può sempre eseguire. Il dominio dei numeri naturali è, dunque, chiuso rispetto all’addizione, alla sottrazione e alla moltiplicazione. Lo zero è l’elemento neutro per l’addizione (e la sottrazione).
In un certo senso !a sottrazione è ora commutativa, dal momento che si ha
b — a = (a — b).
In riferimento all’addizione è dato per ogni numero un ‘elemento inverso’. L’elemento inverso è caratterizzato dal fatto che l’operazione in questione applicata a qualsiasi elemento e al suo inverso dà sempre come risultato l’elemento neutro. La relazione tra elemento ed elemento inverso gode della proprietà simmetrica: se a’ è elemento inverso di a, anche a è elemento inverso di a’.
Si potrebbe chiamare l’elemento inverso anche ‘elemento complementare’ o ‘elemento integrante’ – due elementi inversi `si integrano’ sempre nell’elemento neutro.
Nel dominio dei numeri interi i numeri con Io stesso valore assoluto e diverso segno sono elementi inversi, come per esempio + 4 e — 4; + 4 + (— 4) dà come risultato zero.
Se ora allarghiamo il dominio dei numeri interi al dominio più vasto dei numeri razionali, si hanno in più le seguenti possibilità:
1) Anche la divisione è ora eseguibile senza eccezioni. Il dominio dei numeri razionali è dunque chiuso rispetto all’addizione, alla sottrazione, alla moltiplicazione e alla divisione.
2) Anche in riferimento alla divisione esiste per ogni numero il suo corrispondente ‘inverso’. Quest’ultimo viene indicato come il ‘reciproco’.
Per il numero intero a l’inverso, o reciproco, è ![]() , per la frazione
, per la frazione ![]() esso è
esso è ![]() .
.
a
Che qui si tratti di elementi inversi secondo la definizione data sopra, risulta dal fatto che numeri reciproci moltiplicati tra loro, danno come risultato sempre l’elemento neutro della moltiplicazione, cioè 1:
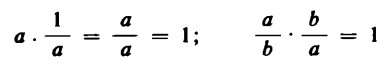
Nell’ambito dei numeri reali si può sempre estrarre la radice quadrata dei numeri positivi, nell’ambito dei numeri complessi si può sempre estrarre anche quella dei numeri negativi.
Ora, i matematici hanno dato determinati nomi a quelle strutture nelle quali viene soddisfatto un determinato numero delle condizioni sopraddette. È degno di nota il fatto che questi nomi coincidono con termini usati per strutture non necessariamente definite sui numeri naturali, interi, razionali, reali, ecc.
La ragione è la seguente. Queste strutture sono da intendersi come entità astratte; in altri termini, esse non sono definite necessariamente sui numeri, ma lo possono essere su universi qualsiasi di elementi, a patto che questi ultimi godano di particolari proprietà e relazioni. La prima struttura non definita sui numeri che abbiamo incontrato è la struttura definita dalle leggi che governano la moltiplicazione dei segni, e in particolare la seguente regola:
Segni uguali danno ‘più’, segni disuguali danno ‘meno’:
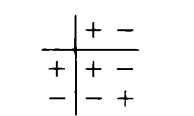
Si tratta di una struttura a due elementi, + e —, e una ‘operazione’, cioè ‘per’.
Se si applica tale operazione al e al —, si ottiene di nuovo + o —,
la ‘società’ è dunque ‘chiusa’. L’operazione è poi commutativa, poiché + per — e — per + danno lo stesso risultato, cioè —.
L’operazione è anche associativa; si hanno infatti le seguenti relazioni:
(+ per —) per + = — per + = + per (— per +) = + per — = —, e così via.
E inoltre:
(— per +) per — = — per — = — per (+ per —) = — per — = +, e così via.
Con tre o più segni si ha in generale: con un numero dispari di segni meno si ha come risultato ‘meno’, con un numero pari di segni ‘meno’ si ha come risultato ‘più’.
Esiste un elemento neutro, cioè + ; infatti, ogni operazione con il + lascia invariato il segno: + per + dà +, + per — dà —.
Elementi inversi non ne esistono; infatti l’operazione applicata a due elementi inversi dovrebbe dare, per definizione, l’elemento neutro. Ma qui l’elemento neutro è + ; se (come viene da supporre) + e — fossero elementi inversi, + per — dovrebbe dare sempre +, il che non è vero.
Ora, a molti matematici interessa di più il complesso delle strutture in generale che il sistema dei numeri in particolare; è per questo che l’elenco delle condizioni che definiscono una struttura non in ogni caso è ispirato alla natura dei numeri. Per esempio, come tra poco vedremo, non esiste nessun termine per contraddistinguere la struttura – cioè la costellazione di rapporti tra i singoli elementi – costituita dai numeri naturali.
PRINCIPALI STRUTTURE
Strutture con una sola operazione +
Gruppo
Un gruppo è caratterizzato dalle seguenti condizioni:
1) il dominio degli elementi è chiuso
2) l’operazione è associativa
3) esiste un elemento neutro
4) esistono elementi inversi
Nessuno dei domini numerici da noi discussi è in questo senso un gruppo.
Se un gruppo soddisfa in più anche la condizione
5) l’operazione è commutativa, allora il gruppo è commutativo o abeliano.
Il dominio dei numeri naturali (senza lo zero), inteso come dominio di elementi più le proprietà delle quali gode (chiusura, associatività, commu-tatività, ma senza elemento neutro per l’addizione e senza elemento inverso per l’addizione e la moltiplicazione) non è né un gruppo né alcuna altra struttura matematica definita e provvista di una denominazione specifica.
Al contrario, il dominio dei numeri interi è un gruppo abeliano. Qui evidentemente si prende in considerazione una sola operazione, l’addizione; la moltiplicazione, al contrario, è fuori considerazione.
Strutture con due operazioni + e •
Anello
L’anello è una struttura numerica caratterizzata dalle seguenti proprietà:
1) l’operazione + è commutativa;
2) l’operazione + è associativa;
3) l’operazione + si può invertire senza restrizioni (sottrazione);
4) l’operazione • non è commutativa, ma è associativa;
5) l’operazione • è distributiva rispetto all’operazione + ; in particolare, tale distributività è commutativa:
a(b + c) = ab + ac
(b + c)a = ba + ca.
Se la seconda operazione • è anche commutativa, allora siamo in presenza di un anello commutativo.
Il dominio dei numeri interi è un anello commutativo (e ciò evidentemente in riferimento ad ambedue le operazioni, addizione e moltiplicazione; in riferimento alla sola addizione è, come abbiamo visto, un gruppo abeliano).
Corpo
Un corpo è un anello commutativo che soddisfa in più la seguente condizione:
6) (3a) anche l’operazione • è sempre invertibile.
Il dominio dei numeri razionali è quindi un corpo.
La sistematica delle definizioni delle strutture matematiche suscita a primo avviso un’impressione di complessità e arbitrarietà, del tutto in contrapposizione con la chiara e lineare costruzione dei nostri domini numerici. Ciò dipende dal fatto che concetti come gruppo, corpo, e anello, possono essere definiti anche su elementi non appartenenti al dominio dei numeri; è chiaro che in tali casi giocano un ruolo essenziale anche caratteristiche diverse da quelle numeriche. Così, ad esempio, la commutatività dell’addizione e della moltiplicazione ci è evidente a tal punto che ci è difficile immaginare operazioni in cui essa non valga. Tuttavia in matematica esistono molti esempi di operazioni, definite su domini non numerici, che non godono della proprietà commutativa.
L’opportunità di definire strutture senza commutatività e di dare loro un nome specifico nasce proprio da questo.
Non è tuttavia opportuno approfondire ulteriormente tale argomento. L’importante era di dare un’idea abbastanza precisa di ciò che si intende in matematica per struttura e in special modo per gruppo, anello e corpo.