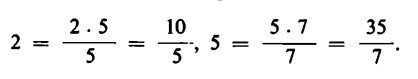In questa guida spieghiamo cosa sono i numeri frazionari.
Se moltiplichiamo tra di loro due numeri a e b, otteniamo il prodotto
ab = c.
Per esempio: 7 per 5 = 35.
Al contrario, non ogni prodotto può essere scomposto in fattori qualsiasi. Per esempio 35 : 7 = 5; ma le divisioni 36 : 7 o 39 : 7 non sono eseguibili.
Possiamo rappresentare questo fatto con la seguente figura:
Quando una divisione non è eseguibile, lo schema corrispondente presenta la caratteristica che la riga inferiore non è completa, ma rimane con dei posti vuoti.
Finché non conosceremo il metodo di soluzione per divisioni del tipo sopra illustrato, scriviamo semplicemente 36 : 7 = 5 resto 1, e 39 : 7 = 5 resto 4.
Il che significa che le prime cinque righe sono complete, mentre l’ultima è incompleta. In altri termini, lo schema ha più di cinque righe di trattini e tuttavia meno di sei.
Dal momento che, per noi, dividere vuol dire ridurre un ‘rettangolo’ di trattini a una sola ‘riga’ o a una sola ‘colonna’, anche in questo caso possiamo dire che 36 : 7 o 39 : 7 dà per risultato 5 e un resto, cioè ‘5 e qualcosa’.
La nostra divisione si può, dunque, scomporre in due parti, in una parte ‘eseguibile’ e in un’operazione sul resto. Ma come eseguire questa operazione sul resto?
Introduciamo per prima cosa un nuovo segno, il segno di frazione, avente la stessa funzione dei due punti per la divisione.
Invece di 10 : 5 possiamo scrivere 
,invece di 35 : 7, 
, e così di seguito.
Poiché, inoltre, conosciamo già i risultati di queste operazioni, possiamo dire:
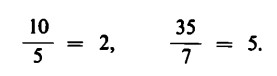
Ma qual è il risultato di 36 : 7 o di 39 : 7? Con l’aiuto del segno di frazione possiamo scrivere semplicemente:
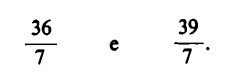
In realtà il valore numerico di queste ultime espressioni, ossia il risultato di cui eravamo in cerca, ci è ancora sconosciuto; infatti, nell’ultimo passaggio non abbiamo fatto altro che sostituire i due punti della divisio-ne con il segno di frazione.
Abbiamo tuttavia già risolto la prima parte della divisione non eseguibile, in quanto abbiamo separato una componente risolvibile. Abbiamo visto, in particolare, che
Ora, però, dobbiamo dividere anche il resto per 7. Otteniamo così:
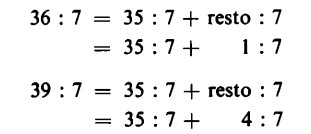
Ovvero, usando il segno di frazione al posto del segno di divisione:
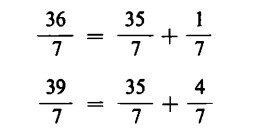
Possiamo davvero scrivere il risultato in questo modo?
Utilizziamo di nuovo variabili numeriche al posto dei singoli numeri. Il numero a (nel nostro esempio, 36 o 39) sia da dividere per il numero b (7). Cerchiamo il più alto multiplo v di b, inferiore ad a, che risolverebbe la nostra divisione (nell’esempio, 35).
Dividiamo innanzitutto questo multiplo per b (nell’esempio, 7); otteniamo così la seguente divisione eseguibile:
A questo punto, possiamo indicare il resto in tal modo esplicitato come differenza fra il numero a e il numero v (nell’esempio, fra 36, ovvero 39, e 35):
a — v (nell’esempio, 36 — 35, ovvero 39 — 35) e dividiamo anche questa differenza per b:
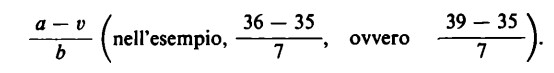
L’intera operazione diventa allora:
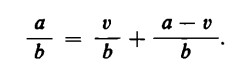
Nell’esempio:
A questo punto rimane ancora da accertare se sia realmente possibile porre
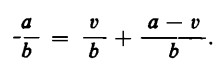
A tale scopo dobbiamo mostrare che anche per la divisione vale la proprietà distributiva rispetto alla somma.
In effetti la distributività della divisione si può derivare immediatamente dalla proprietà distributiva della moltiplicazione. Il metodo da seguire è il seguente:
Sia da dimostrare che
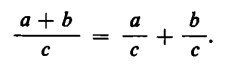
Poniamo innanzitutto:
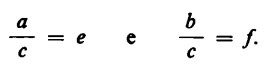
Si ha allora
a = ec e b = fc;
quindi
a + b = ce + cf = c(e + f)
e ancora
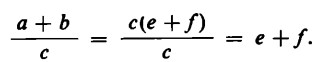
Se si reintroducono a e b sulla parte destra dell’uguaglianza si ottiene:
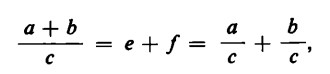
con il che la distributività della divisione è dimostrata.
Se, ora, si toglie da a l’addendo v e si scrive il resto come differenza
a — v, il numero originario a si può esprimere nella maniera seguente:
a = v + (a — v) = v + a – v = a;
infatti, essendo v – v = 0, a rimane anche dalla parte destra.
Ora, per la proprietà distributiva della divisione, possiamo scrivere
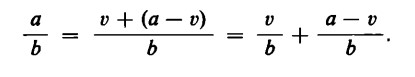
Abbiamo con ciò dimostrato che una divisione con resto 
si può trasformare nella somma di due divisioni, che si ottengono così: si mette in evidenza il più alto multiplo di b inferiore ad a e poi si dividono tale multiplo v e il resto a – v per il divisore b.
Rimane, però, ancora il problema di come trattare il resto.
Si tenga presente quanto segue: il procedimento di scomposizione della nostra divisione consiste nel prendere tutte le volte il più alto multiplo v del divisore b che ‘vada bene’. La restante differenza a – v sarà quindi sempre minore di b; a – v rappresenta inoltre l’ammontare dei segni numerici che si trovano nella fila inferiore incompleta dello schema che rappresenta il prodotto.
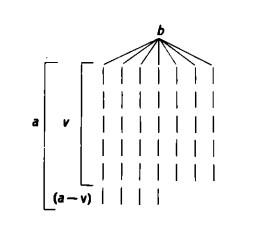
Nell’espressione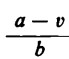 
, in cui a — v rappresenta il resto che deve essere ancora diviso (i trattini della riga inferiore) e b il divisore (la lunghezza delle righe normali), a – v è quindi sempre minore di b; ad esempio,
Che significano, ora, le espressioni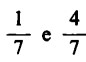 
?
Immaginiamo di dover dividere una mela (ovvero 4 mele) tra 7 bambini. Questo è un caso pratico di applicazione della divisione.
significano, ad esempio, l’operazione del dividere una mela (ovvero 4 mele) in ‘parti uguali’ a ciascuno dei 7 bambini.
Se avessimo esattamente 7 mele, a ogni bambino toccherebbe una mela. Dal momento, però, che il resto è minore di 7 mele, a ogni bambino tocca solo una parte di una mela intera.
Che porzione di mela toccherà a ogni bambino? La seguente riflessione ce lo può suggerire. Se la riga che rappresenta il resto nel nostro schema del prodotto fosse una riga completa, ossia contenesse 7 segni numerici, corrispondenti ad altrettante mele, ogni bambino avrebbe come ‘resto’ una mela intera:
Siccome, tuttavia, il nostro resto è pari a una (ovvero quattro) mele, il resto da dividere in parti uguali si limita a un trattino (ovvero quattro) nella riga che rappresenta il resto:
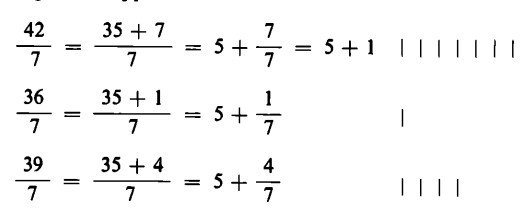
In pratica la nostra ripartizione consiste nel dividere la (o ciascuna) mela restante in sette parti uguali e nel distribuire le parti risultanti a ciascun bambino, l’una dopo l’altra e in modo uniforme.
Chiamiamo ‘un settimo’ e indichiamo col simbolo 1/7 la frazione di mela divisa in sette parti uguali.
Se ci sono quattro mele da dividere una alla volta in sette parti uguali, a ogni bambino toccherà sempre un settimo di mela, ma per quattro volte, e cioè
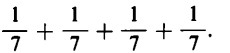
Per la legge della distributività possiamo anche scrivere:
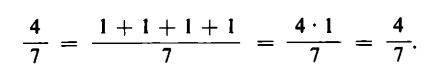
Se vogliamo risolvere la divisione 39 : 7, dobbiamo eseguire, dunque, i seguenti passi:
a) cerchiamo il più alto multiplo di 7 inferiore a 39, vale a dire 35;
b) dividiamo 35 per 7 e otteniamo 5;
c) troviamo il ‘resto’ 39 — 35 = 4 e dividiamo anche il resto per 7.
A questo punto si procede, in pratica, dividendo unità per unità per 7 e sommando i risultati:
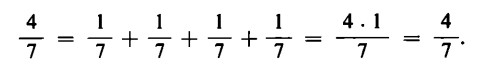
39 : 7 è dunque uguale a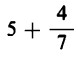 
Generalizzando:
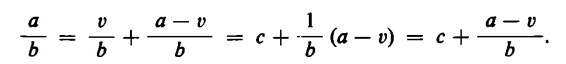
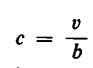designa qui la soluzione in interi della divisione 
che abbiamo in precedenza separato.
Siamo così arrivati al risultato che ogni numero può essere diviso per un qualsiasi altro.
Almeno per approssimazione, è possibile trovare il risultato anche nel caso in cui la divisione non è eseguibile senza resto, ossia anche nel caso in cui il quoziente non è un numero di quelli finora conosciuti, vale a dire rappresentabili mediante una figura numerica: basta trovare anzitutto il numero naturale più vicino al risultato da ottenere ma ad esso inferiore, poi aggiungere una ‘frazione’ minore di l, pari alla differenza tra il quoziente da cercare e il numero naturale trovato per approssimazione.
Possiamo chiamare ‘frazione’ il numero cercato, dal momento che per ottenerlo abbiamo dovuto, per così dire, ‘frangere’, ‘tagliare’, ‘spezzare’ o comunque dividere in parti gli oggetti (nell’esempio, le mele).
Se non ci interessa il ‘valore approssimato’ di una frazione, possiamo scrivere, anziché 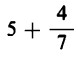il numero 
semplicemente. Per motivi analoghi, non serve calcolare il valore di una frazione, come per esempio 
nella quale il ‘numero che sta sopra’ è minore del ‘numero che sta sotto’, in quanto il suo ‘valore approssimato’ è minore di uno.
Esempio: 8 mele siano da dividere tra 29 bambini. A questo scopo dividiamo ognuna delle 8 mele in 29 parti, dopodiché consegniamo uno di questi ventinovesimi ad ognuno dei 29 bambini per otto volte di seguito.
Il numero che sta al di sopra del segno fratto di una frazione si chiama numeratore, il numero che sta al di sotto si chiama, invece, denominatore. Se il numeratore è più grande del denominatore, vale a dire se il ‘valore approssimato’ della frazione è più grande di uno, la frazione si dice impropria; se, al contrario, il denominatore è più grande del numeratore, vale a dire se il ‘valore approssimato’ della frazione è minore di uno, la frazione si dice propria (in una frazione impropria si può trovare il massimo multiplo del denominatore inferiore al numeratore, in una frazione propria, invece, no).
I nuovi numeri introdotti si chiamano numeri frazionari. In contrapposizione ad essi, i numeri naturali di cui abbiamo parlato finora si chiamano anche numeri interi.
I numeri interi costituiscono un caso speciale dei numeri frazionari. Infatti ogni numero intero si può scrivere sotto forma di frazione; tale frazione si ottiene moltiplicando il numero intero dato per un numero qualsiasi e dividendo il prodotto ottenuto per lo stesso numero; per esempio
