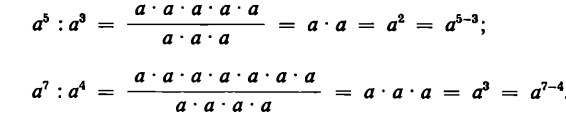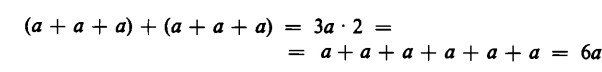Elevazione a Potenza con Esponenti Negativi e Frazionari

In questa guida spieghiamo come risolvere le elevazioni a potenza con esponenti negativi e frazionari.

Elevazione a potenza come composizione di fattori

Come la moltiplicazione nasce dall’addizione ripetuta dello stesso addendo. così l’elevazione a potenza nasce dalla moltiplicazione ripetuta dello stesso fattore.
Se prima potevamo scrivere le espressioni a, a + a, a + a + a, a + a + +a+ a, a+a+a+a+ a, ….+ a, che significano l’addendo a preso 1, 2, 3, 4, …. n volte, nella forma abbreviata la, 2a, 3a, 4a, …. na,
in maniera del tutto analoga possiamo scrivere le espressioni a, a•a, a•a•a, a•a•a•a, a•a•a•a•a,….a, che significano il fattore a preso , 2, 3, 4, …. n volte, nella forma abbreviata a¹, a², a³, . . aⁿ. Il fattore preso una volta sola si può scrivere nella forma a¹, così come abbiamo espresso l’addendo a preso una volta sola nella forma 1a.

L’elevazione a potenza gode di interessanti proprietà che non hanno un corrispettivo a livelli più bassi del calcolo.
Se si moltiplica a per a, si ha come risultato a^{1 •} a¹ = a².
Se si moltiplica a² per a³, si ha (a•a)•(a•a•a)= a-a-a-a•a = a⁵.
Se si moltiplica a³ per a⁴, si ottiene ancora (a • a • a) • (a • a • a • a) = = a•a•a•a•a•a•a = a⁷.
Ne segue la regola generale per cui il prodotto di potenze aventi la stessa base è una potenza che ha per base la stessa base e per esponente la somma degli esponenti.
Si può quindi trasformare un calcolo di tipo superiore (il moltiplicare) in uno di tipo inferiore (l’addizionare). Infatti l’elevazione a potenza di un certo numero a non è altro che una scrittura stenografica per esprimere la moltiplicazione del numero a n volte per sè stesso; in tal modo, la ‘somma’ degli esponenti coincide in realtà con una moltiplicazione (in effetti, si è fatto qui tacito uso della proprietà associativa della moltiplicazione, per cui la moltiplicazione `dentro parentesi’ e quella `fuori parentesi’ si equivalgono: (a•a)•(a•a•a)= (a•a•a•a•a).
Una proprietà analoga alla precedente vale anche per la divisione di potenze. Si possono infatti eseguire, per così dire, `all’indietro’ le nostre operazioni e ottenere:

La divisione di potenze si può ridurre pertanto alla sottrazione degli esponenti.
Questo principio consistente nella `trasposizione da un livello superiore a un livello inferiore’ si può applicare anche nel caso specifico dell’elevazione a potenza.
Il numero 3a, ovvero a + a + a, si può raddoppiare ponendo il doppio di addendi a, cioè

Il corrispondente si ha per l’elevazione a potenza. Elevare al quadrato un numero vuol dire moltiplicare quel numero per sè stesso, cioè porlo per due volte come fattore.
Se ora poniamo per due volte come fattore a³=a•a• a, abbiamo: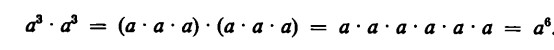

Poiché, per l’associatività della moltiplicazione, l’operazione `dentro le parentesi’ equivale a quella ‘fuori parentesi’, elevare al quadrato delle potenze coincide col raddoppiare il numero di volte per cui è posto il fattore che genera la potenza stessa.
In tal modo a², elevato alla terza potenza, dà per risultato la potenza

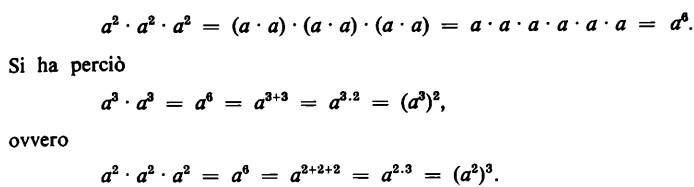
La potenza di una potenza è, dunque, una potenza che ha per base la stessa base e per esponente il prodotto degli esponenti.

Per l’estrazione di radice vale l’operazione inversa. Estrarre la radice di un numero significa infatti trovare per un dato numero il numero che, moltiplicato per sé stesso, dà il numero dato. Dunque, per trovare la radice quadrata di a⁶, basta dividere l’esponente 6 per 2; si ottengono così due fattori uguali, ciascuno dei quali è a posto per 3 volte come fattore:

Similmente si può ricavare la radice cubica di di

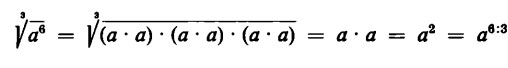
La riduzione della moltiplicazione e della divisione fra potenze di base uguale all’addizione e alla sottrazione dei rispettivi esponenti, nonché la riduzione dell’elevazione a potenza e dell’estrazione di radice di potenze alla moltiplicazione e alla divisione degli esponenti in questione, suggerisce di applicare anche al calcolo sugli esponenti l’ampliamento, a noi già noto, del campo numerico, ovvero di illustrare gli esponenti negativi e frazionari.

Esponenti negativi

Supponiamo di dividere successivamente la potenza a⁶ per a, a², a³, a⁴. Otteniamo come risultati a⁵, a⁴, a³ e infine a². Infatti:

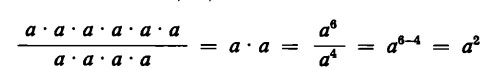
Dividiamo ora a⁶ per a⁵. Otteniamo:

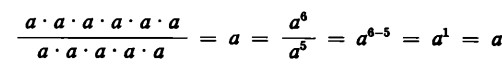
Ma che cosa otteniamo dividendo a⁶ per a⁶? Sappiamo che ogni numero diviso per sè stesso dà 1. Dunque

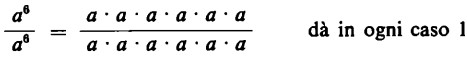
Siccome però, al posto di a⁶ : a³, possiamo scrivere a^6-6 e, al posto di 6 – 6, zero, avremo a⁰ = 1.
Possiamo pertanto porre a° = l, dal momento che tutte le volte che si divide per a si toglie un’unità all’esponente: se, dunque, si divide a² per a si ottiene a = a¹, e se si divide a = a¹ per a, si ottiene

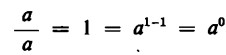
L’espressione a⁰ = 1 non è dunque, come alcuni autori sembrano voler far credere, una mera convenzione arbitraria ma è una conseguenza necessaria dalla nostra definizione di divisione di potenze (per lo meno risulta chiaramente che l’uguaglianza a⁰ = 1 è in ogni caso ‘più giusta’ di a⁰ = a o a⁰ = 0).

Se, a questo punto, dividiamo a⁶ per a⁷, o a per a² o a⁰ per a, il che dà sempre lo stesso risultato, otteniamo:

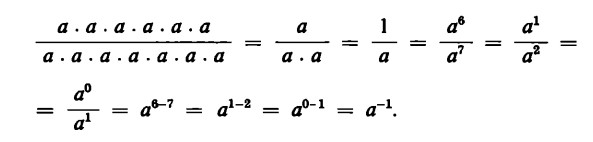
a^-1 è dunque uguale a una frazione nel cui denominatore si trova un fattore a in più rispetto ai fattori a contenuti nel numeratore, e che semplificata dà sempre .

In maniera analoga avremo 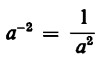quando il denominatore è a x a = a² volte ‘più grande’ del numeratore, il che dà sempre, semplificando, , e così via.
Una potenza con esponente negativo ha dunque il seguente significato: il suo valore è pari a quello di una frazione avente per numeratore l’unità e per denominatore una potenza con la medesima base e il corrispondente esponente con segno positivo. Con esponente generico vale la relazione:

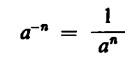
Se, per esempio, poniamo come base a = 10, si hanno le seguenti uguaglianze:

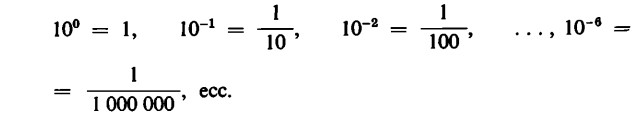
Potenze con esponenti negativi sono, dunque, l’inverso delle rispettive potenze con esponenti positivi.

Esponenti frazionari

Similmente, possiamo allargare il dominio delle potenze, che si ricavano dalla divisione degli esponenti.
Se dividiamo un esponente per 2 otteniamo, come abbiamo visto, la radice quadrata.
Così a⁴ è la radice quadrata di a⁸, a³ quella di a⁶, a² quella di a⁴ e a¹ = a quella di a²:

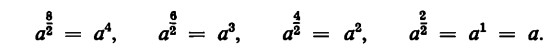
Dunque, mentre da un lato sappiamo che, dividendo l’esponente di a = a¹, vale a dire 1, per 2, si ottiene , dall’altro sappiamo che, sempre dividendo l’esponente di a = a¹ per 2, si ottiene la radice quadrata di a, vale a dire √a.
è allora uguale alla radice di a, proprio come è la radice quadrata di a⁴ o a = a¹ è la radice quadrata di a².

Analogamente si ha che , come ,ecc.
In generale si ha dunque: . In altri termini, le potenze con esponente frazionario sono particolari radici.

Riduzione delle operazioni mediante logaritmi

Gli esponenti delle potenze si possono sommare e moltiplicare senza limiti, come pure sottrarre e dividere. In ogni caso, è possibile ‘ridurre’, per così dire, i calcoli a un livello di complessità inferiore: dalla moltiplicazione si può passare all’addizione, dalla divisione alla sottrazione, dall’elevazione a potenza alla moltiplicazione e dall’estrazione di radice alla divisione. La possibilità di una tale ‘riduzione’ ha portato alla scoperta dí un geniale metodo di calcolo numerico: il calcolo dei logaritmi.
Il ‘logaritmo’ non è altro che l’esponente di una data potenza, il numero al quale essa è elevata.
Il calcolo dei logaritmi si fonda sul seguente principio. Si suppone che il numero, sul quale si debbono operare dei calcoli, sia una potenza di una certa base, ad esempio 10; il numero si può dunque esprimere nella forma 10^x. Il numero x è il logaritmo di quel numero in base 10. Il ‘logaritmo di 10’ è, ad esempio, 1, il ‘logaritmo di 100’ è 2, dal momento che 10¹ = 10 e 10² = 100.
I logaritmi dei numeri dall’11 al 99 sono degli ‘strani’ numeri compresi tra 1 e 2, ad esempio:

Per moltiplicare due numeri, basta sommarne i rispettivi logaritmi. La somma è il logaritmo del prodotto.
Per esempio

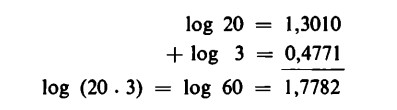
In pratica questo calcolo si esegue con l’aiuto delle tavole logaritmiche nel seguente modo: si cercano innanzitutto i logaritmi dei due fattori, li si somma, dopodiché si va a cercare il numero corrispondente alla somma dei logaritmi. Questo numero è il prodotto cercato (si osservi che l’inesattezza della somma sopra riportata dipende dal fatto che i logaritmi, in quanto numeri irrazionali, hanno un numero infinito di cifre decimali, per cui si arrotondano nell’ultima cifra).
I logaritmi in base 10 godono di un’interessante proprietà, che merita di essere qui ricordata: dal momento che nel sistema decimale i numeri costituiti dalla stessa successione di cifre, come 0,623 — 6,23 — 62,3 — 623 — 6230 si distinguono solo per il fattore 10ⁿ e poiché il logaritmo di questo fattore è n (numero intero), i logaritmi dei numeri costituiti dalle stesse cifre si differenziano solo per il numero che si trova a sinistra della virgola. Così i logaritmi di 0,623, ecc. sono:

Sulle tavole dei logaritmi si trovano, dunque, solo le cifre decimali senza la virgola. Il numero intero da mettere a sinistra della virgola si ricava facilmente dalle potenze intere di 10: il logaritmo di un numero compreso tra 10 e 100 sarà, per esempio, l, …
Un risultato analogo a quello precedente vale anche per l’elevazione al quadrato e per l’estrazione di radice: infatti, per elevare un numero alla seconda potenza e per estrarne la radice quadrata, basta raddoppiare ovvero dimezzare il logaritmo di quel numero. Così log 9 è 0,9542 e log 3 è 0,4771, che è evidentemente la metà del primo.
In linea di principio, un regolo calcolatore funziona come la tabella dei logaritmi.
Evidentemente ci si può costruire un regolo anche senza logaritmi, per esempio un regolo che serva soltanto per sommare e sottrarre. A tale scopo basta prendere due semplici regoli. Se ora vogliamo sommare 10 + 6, non dobbiamo far altro che disporre i regoli in modo tale che il punto O dell’uno si trovi in corrispondenza del punto 10 dell’altro e leggere la somma 16 sul secondo regolo in corrispondenza del numero 6 del primo:

Si interpretano dunque i numeri e la loro somma su segmenti, così come avviene quando si rappresenta l’insieme dei numeri sull’insieme dei punti della retta numerica. Questa è la forma più semplice di calcolatore analogico, come è noto dalle applicazioni tecniche della teoria dell’informazione.
Se vogliamo utilizzare il regolo calcolatore anche per moltiplicare, dovremo solo sommare gli esponenti (logaritmi).
A tale scopo basta considerare i numeri sul regolo come esponenti e associare ad essi quei numeri che corrispondono a potenze di una data base. Per ragioni di semplicità, prendiamo, ad esempio, come base il 2; scriviamo sul regolo al posto dei numeri n le potenze corrispondenti in base 2, 2ⁿ:

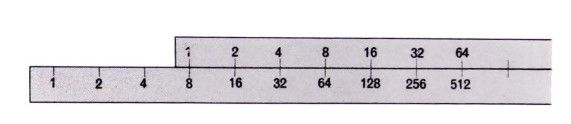
Naturalmente dobbiamo calcolarci anche i corrispondenti valori intermedi, il che ha come conseguenza che, spostandosi da sinistra verso destra, l’unità di misura diventa sempre più piccola, mentre i numeri diventano man mano più compatti. Risparmiamoci questa complicazione e calcoliamo, sempre per ragioni di semplicità, solo con potenze di 2. Per eseguire il prodotto 8 x 32 basterà così porre l’1 del regolo superiore accanto all’8 di quello inferiore e poi trovare, in corrispondenza del numero 32 del regolo superiore, il prodotto cercato, che è 256. I segmenti che abbiamo disposto uno accanto all’altro non rappresentano, infatti, direttamente le potenze, ma gli esponenti delle potenze stesse.

Il regolo calcolatore è quindi una specie di tavola logaritmica ‘simultanea’. Sommiamo esponenti ma leggiamo direttamente i numeri da moltiplicare.
Il punto ‘zero’ di ogni regolo è l’1, dal momento che per ogni numero, ovvero per ogni base logaritmica, a⁰ = 1.
Per elevare al quadrato o estrarre la radice quadrata, basta raddoppiare ovvero dimezzare lunghezze. Per eseguire tali operazioni non c’è bisogno di un regolo calcolatore scorrevole, basta una semplice riga a due scale che stanno nel rapporto di I a 2. Su questa riga quadrati e radici giacciono sempre l’uno contro l’altra