In questa guida spieghiamo le proprietà associativa, commutativa e distributiva della moltiplicazione.
Abbiamo già studiato due operazioni: l’addizione e la sottrazione. Abbiamo visto poi come la sottrazione sia l’operazione inversa dell’addizione.
Anche la moltiplicazione deriva dall’addizione; e questa è una prova in più a favore della tesi che l’addizione è in fondo l’unica operazione computistica, della quale le altre non sono che casi speciali.
Che cosa vuol dire moltiplicazione? Nell’addizione, gli addendi a e b sono numeri qualsiasi, perciò anche diversi fra loro, che composti danno il nuovo numero c. Al contrario, la moltiplicazione è un’addizione ripetuta dello stesso numero. Anziché il caso generale a + b, si ha qui solo il caso speciale a + a.
Un esempio di moltiplicazione è il seguente. Ci sono due gatte: ogni gatta ha tre piccoli; quanti piccoli ci sono in tutto?
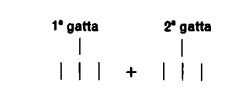
Il problema si può naturalmente risolvere con l’addizione: 3 + 3 = 6. Sentire tale problema come caso di addizione e non ancora di moltiplicazione è naturale, dal momento che la probabilità che due numeri piccoli siano uguali piuttosto che diversi, è pur sempre assai grande. Se per esempio giochiamo con due dadi, la probabilità che ambedue i dadi esibiscano la stessa faccia è pari a 1 / 6. Casi di addizione con addendi uguali sono dunque in questo campo molto normali.
Le cose andrebbero diversamente nel caso in cui avessimo nove gatte e ognuna di queste mettesse al mondo tre piccoli. In questo caso non saremmo disposti ad applicare l’addizione. La frequente ripetizione dello stesso numero ci spinge infatti in maniera affatto naturale a cercare un procedimento computistico ‘superiore’, un procedimento cioè che sfrutti il fatto che gli addendi sono uguali.
Torniamo ora alle nostre sequenze di trattini.
Visto che gli addendi dell’addizione in questione sono tutti uguali, è possibile stabilire una corrispondenza biunivoca tra di loro. Illustriamo tale concetto, disponendo d’ora in poi tutte le cifre una sotto l’altra:
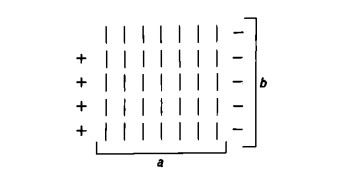
La figura sopra illustrata è una rappresentazione grafica dell’operazione 7 + 7 + 7 + 7 + 7.
In ogni riga compare sempre lo stesso numero; niente ci vieta pertanto di considerare quest’ultimo come un’unità e di contare, di conseguenza, le volte in cui esso ricorre come addendo. In cifre arabe abbiamo a che fare con cinque `sette’; ma l’uso di tali cifre non è essenziale ai nostri scopi e serve solo a scopo di illustrazione.
La figura sopra ci mostra, dunque, cinque volte la cifra ‘sette’. Le cifre sono scritte in colonna, in modo che i segni numerici risultano anch’essi allineati uno sotto l’altro. Col metodo della corrispondenza possiamo facilmente effettuare la verifica che le cinque cifre sono effettivamente uguali.
A questo punto possiamo facilmente contare non soltanto i trattini di ogni cifra, ma anche le cifre stesse. A questo scopo basta contare, anziché da sinistra verso destra, dall’alto verso il basso. Rappresentiamo graficamente tale procedimento associando a ogni cifra, sulla destra, un tratto orizzontale. Contiamo questi tratti orizzontali dall’alto verso il basso come una sequenza di segni numerici ruotata verso destra di 90°.
Designiamo ora il numero da cui siamo partiti con a e con b il numero delle ripetizioni di a. Moltiplicare a per b significa allora porre a ‘b volte’, esaurirne tutte le ricorrenze, contiamo quindi quante sono le ricorrenze di a e designiamo tale risultato direttamente con l’espressione ‘a per b’. Il numero ‘a per b’ si definisce prodotto di a e b. a e b sono i fattori della moltiplicazione. Così, il prodotto di 3 e 9 è 27, di 7 e 5 è 35.
Naturalmente, conoscendo soltanto la successione dei numerali, non possiamo calcolare direttamente il risultato di una moltiplicazione. Finché sapremo solo sommare e non moltiplicare, il nostro schema per la moltiplicazione non ci sarà di nessun aiuto. Non ci resterà che enumerare riga per riga i trattini come per l’addizione. Alla fine giungeremo all’ultimo trattino a destra in basso, che sarà contraddistinto dal numerale ‘trentacinque’.
Per moltiplicare direttamente c’è bisogno di qualcosa di più del semplice contare: dobbiamo imparare a memoria i prodotti di un certo insieme fondamentale di numeri che ricorrono di frequente. Tale processo di apprendimento mnemonico avviene, come è noto, nella seguente maniera: iniziando dall’uno, prendiamo ogni numero uno dopo l’altro, una volta, due volte, tre volte, ecc. e impariamo a memoria il risultato. L’elenco di tutti questi prodotti è noto come ‘tavola pitagorica’.
Nella nostra notazione per trattini la tavola pitagorica si presenta cosi
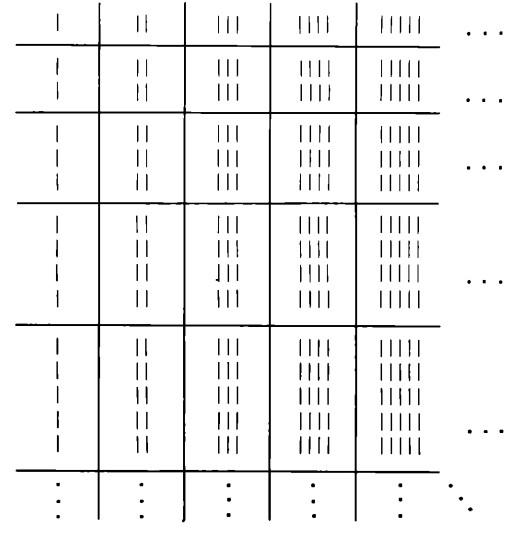
In altre parole, la moltiplicazione si può spiegare nella maniera seguente: abbiamo un determinato numero — ad esempio il numero dei piccoli di una gatta. Questo numero ricorre più volte — nel senso che più gatte hanno lo stesso numero di piccoli. Se dunque sette gatte hanno ognuna cinque piccoli, in tutto ci sono sette per cinque, ossia trentacinque piccoli.
Indice
Proprietà Commutativa della Moltiplicazione
Anche in riferimento alla moltiplicazione possiamo chiederci se i fattori sono mutuamente interscambiabili; in altre parole: a per b è uguale a b per a?
La risposta positiva non è immediatamente evidente. Supponiamo che sette gatte abbiano messo al mondo ciascuna cinque piccoli. Ebbene, per quale ragione il numero complessivo dei piccoli dovrebbe essere senz’altro uguale al numero che ne risulta nel caso di cinque gatte che mettono al mondo sette piccoli ciascuna?
Una semplice riflessione ci suggerisce che, in effetti, a per b è uguale a b per a. Quindi a gatte che hanno messo al mondo un numero b di piccoli ciascuna hanno esattamente altrettanti piccoli quanti ne hanno b gatte che hanno messo al mondo a piccoli ciascuna.
Consideriamo ancora una volta il nostro schema della moltiplicazione:
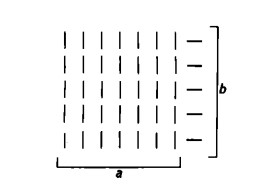
Finora abbiamo contato il totale dei trattini riga per riga in senso orizzontale. Come risultato abbiamo ottenuto il numero a per b volte. Ora, poiché i trattini sono fra loro ordinati anche in colonne, è possibile contarli anche colonna per colonna, ovvero in senso verticale.
Ogni colonna ha b trattini e, inoltre, ci sono a colonne. Di conseguenza, contando in senso verticale, otteniamo il numero b per a volte. Ma il numero dei trattini è sempre lo stesso. Pertanto il numero a per b coincide con il numero b per a.
Se come segni numerici usiamo sassolini o circoletti, anziché fiammiferi o trattini, il risultato è ancora più chiaro
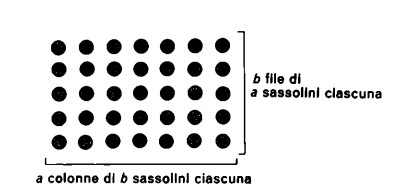
La ragione della commutatività della moltiplicazione è, dunque, la seguente: tutte te righe ricorrenti nella figura sono di pari lunghezza e lo stesso vale per le colonne.
Ne segue che ogni figura si può leggere sia in senso orizzontale (per righe) sia in senso verticale (per colonne).
Anche qui vale quello che si diceva sopra: non si tratta di una illecita ‘visualizzazione’, ma di una conseguenza della nostra concezione operativa del calcolo con segni numerici. La validità della nostra dimostrazione riposa essenzialmente sulla possibilità di far corrispondere in maniera univoca segni numerici a segni numerici, possibilità che, pur essendo indipendente da contenuti intuitivi, è profondamente radicata nella pratica quotidiana.
Ancora una precisazione: la commutatività della moltiplicazione vale anche per numeri grandi a piacere. Infatti, per quanto grandi siano tali numeri, siamo sempre in grado, almeno in linea di principio, di costruire il nostro schema ‘rettangolare’ della moltiplicazione.
Proprietà Associativa della Moltiplicazione
Come per l’addizione, anche per la moltiplicazione ci si può porre la questione se è possibile moltiplicare tre numeri, se è possibile cioè calcolare il prodotto della moltiplicazione non solo del numero a per il numero b, ma anche del numero a per il numero c.
Cosa significa ‘a per b per c’? Esso è il risultato della moltiplicazione del prodotto a per b, già trovato, per c.
Abbiamo già rappresentato graficamente il prodotto a per b. Tale rappresentazione era una figura bidimensionale, una specie di rettangolo, ottenuta scrivendo b volte dall’alto verso il basso la sequenza lineare rappresentante il numero a. In maniera simile possiamo rappresentare il prodotto `a per b per c’; basta riprodurre c volte nello spazio la figura a due dimensioni che rappresenta a per b. Si ottiene così una specie di parallelepipedo.
Se ora, per ragioni di semplicità, consideriamo i segni numerici come costituiti da cubetti tutti uguali, otteniamo un solido geometrico del tipo
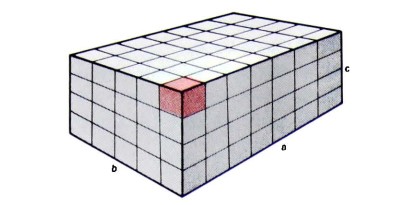
La ‘base’ di questo parallelepipedo rappresenta il prodotto a per b. Il fattore c, per il quale si moltiplica il prodotto a per b, è rappresentato a sua volta dall’altezza del parallelepipedo stesso. Il volume del parallelepipedo è pertanto la rappresentazione del prodotto a per h per c.
Osserviamo di nuovo che la costruzione della figura non si basa su una forma di intuizione geometrica. I cubetti del parallelepipedo rappresentano infatti dei segni numerici arbitrari, che, in quanto vengono messi in corrispondenza nel modo che abbiamo già chiarito a proposito del modello a due dimensioni, hanno un significato puramente operativo.
A questo punto è facile dimostrare anche la legge dell’associatività; dobbiamo mostrare che (a per b) per c = a per (b per c) = b per (a per c). In primo luogo basta costruire il parallelepipedo disponendo, per cosi dire, degli strati orizzontali uno sopra l’altro; poi pensare il parallelepipedo costituito da strati verticali che si susseguono uno dietro l’altro in prospettiva `da sinistra verso destra’, e quindi da strati sempre verticali ma che si susseguono in prospettiva `da destra verso sinistra’. La figura chiarisce da sola il concetto.
Univocità destra
Anche la moltiplicazione è ‘univoca a destra’. Cioè: due numeri a e b danno origine a un prodotto univocamente determinato. Ma ciò non significa che il prodotto c si possa ottenere solo a partire dai fattori a e b. Si consideri il seguente schema
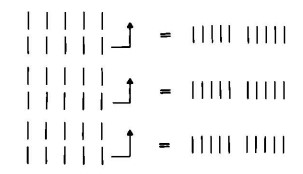
Questo schema consiste di sei righe costituite ciascuna da cinque segni numerici. Spostiamo ora ogni riga di posto pari accanto a quella che vi si trova sopra. In tal modo otteniamo tre righe costituite ognuna da due per cinque, ovvero dieci segni numerici, dal che risulta che 5 per 6 = 10 per 3 = 30.
Lo stesso numero può dunque essere il prodotto di diverse coppie di fattori. Si pensi al numero 60:
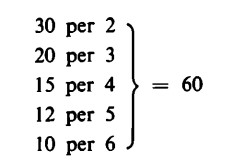
(senza considerare le permutazioni dei fattori).
È chiaro, a questo punto, che anche la moltiplicazione è univocamente determinata a destra: tutte le coppie che stanno dalla parte sinistra conducono univocamente allo stesso prodotto, per l’appunto 60; questo prodotto al contrario non può essere univocamente scomposto in due fattori, ma sono possibili diverse scomposizioni in fattori.
Proprietà Distributiva della Moltiplicazione
Dopo aver introdotto l’operazione dell’addizione e quella della moltiplicazione, è naturale chiedersi se tra di esse esistano particolari relazioni. In caso positivo è poi opportuno precisarne il contenuto.
A tal fine, proviamo a moltiplicare la somma a + b per un terzo numero. La nostra notazione per trattini ci suggerisce il seguente schema:
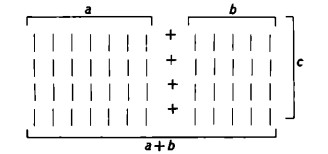
Non è difficile riconoscere che lo schema nel suo complesso costituisce la rappresentazione del prodotto (a + b) per c, mentre il lato sinistro dello schema rappresenta il prodotto a per c e il lato destro il prodotto b per c.
L’intero schema (a + b) per c costituisce dunque la somma di a per c e di b per c, dal che segue la legge della distributività della moltiplicazione rispetto all’addizione:
(a + b) c = ac + bc.
Il termine `distributività’ deriva dall’operazione del `distribuire’; il numero c viene, per così dire, ‘distribuito’ su a e su b, come mostra la parte destra dell’uguaglianza.
La legge della distributività ha una parte essenziale nel ‘calcolo con le parentesi’. Dalla semplice legge della distributività possiamo, per esempio, ricavare la ‘legge della moltiplicazione con parentesi’
(a + b)(c + d) = ac + ad + bc + bd.
Infatti, ponendo (c + d) = C, otteniamo:
(a + b) (c + d) = (a + b) C
(a + b) C = aC bC
= a(c + d) + b(c + d)
= ac + ad + bc bd.
Nell’ultima dimostrazione abbiamo fatto tacitamente uso della commu-tatività della moltiplicazione; in base a quest’ultima, infatti, possiamo accettare la validità non soltanto di (a + b) c = ac + bc, ma anche di a (c + d) = ac + ad, dove, come si può ben vedere, l’espressione in parentesi sta una volta a sinistra e una volta a destra del fattore singolo.
Che cosa possiamo dire nei confronti della distribuzione inversa
(a per b) + c?
Tracciamo il seguente schema di trattini
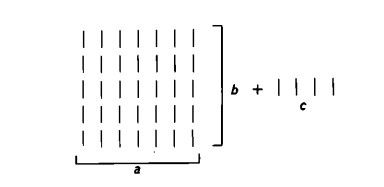
Vediamo subito che non è possibile andare oltre: c non si trova in nessun particolare rapporto con il resto dello schema. Quest’ultimo non rappresenta altro che una somma i cui addendi sono, da una parte, a per b e, dall’altra, c, somma questa non diversa in linea di principio dal caso più semplice a + b. Pertanto, per determinare il valore di (a per b) + c, non rimane che aggiungere c al valore di a per b, calcolato a parte.
Non vale dunque la relazione:
(a per b) + c = (a + c) (b + c),
la quale sarebbe l’esatto corrispettivo della legge di distribuzione
(a + b) c = ac + bc,
scambiando il segno dell’addizione con quello della moltiplicazione. Infatti il calcolo della parte destra della nostra distribuzione fittizia darebbe come risultato ab + ac + bc + cc, oppure, evidenziando il c, ab + c (a 4- b + c); quest’ultima, però, è un’espressione diversa da ab + c, parte sinistra della nostra distribuzione fittizia.
Abbiamo analizzato a fondo la definizione di legge della distribuzione `inversa’, perché non è immediatamente evidente che essa non valga. Nella cosiddetta ‘algebra degli insiemi’, che più avanti ci proponiamo di affrontare, essa infatti vale.