In questa guida spieghiamo la proprietà commutativa della sottrazione.
Abbiamo già incontrato il metodo della cancellazione di segni numerici parlando delle proprietà dell’addizione. Questo metodo si può ora applicare per introdurre il secondo tipo di operazione tra numeri, la sottrazione.
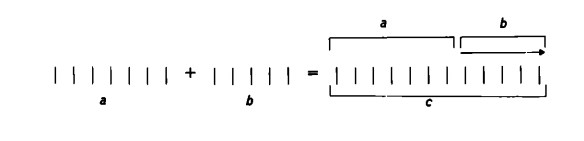
L’addizione permette di ricavare la somma c di due numeri dati a e b
Ebbene, dopo aver costruito il numero c possiamo cancellare i segni numerici che costituiscono b. Questo procedimento si chiama sottrazione. Ciò che rimane dopo l’operazione è il numero a. Se dunque cancelliamo b da c, otteniamo di nuovo a:
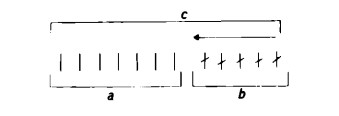
Indichiamo l’operazione del sottrarre col segno ‘meno’, -, e scriviamo di conseguenza:
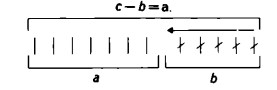
La sottrazione è dunque, per così dire, l’inverso dell’addizione.
Se contiamo di seguito al numero a il numero b, otteniamo il numero c; dopodiché, se togliamo (o cancelliamo) dal numero c il numero b, otteniamo di nuovo il numero a.
a + b = c
c – b = a.
Visto che , poi, per la legge della commutatività l’ordine con in compaiono a e b si può invertire, è possibile togliere con pari legittimità a da c e ottenere b come resto:
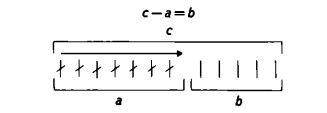
In ogni caso si ha: ‘ciò che viene tolto’ e il ‘resto’ danno la somma originaria; infatti ciò che viene tolto e il resto non sono altro che il numero a e il numero b, numeri che addizionati danno come risultato il numero c. Di conseguenza, è in linea di principio indifferente quali dei due numeri consideriamo il numero ‘tolto’ e quale il numero ‘rimanente’.
Di solito, il numero ‘rimanente’ (nel nostro primo esempio, a) si chiama differenza; ma naturalmente si potrebbe considerare a ragione come ‘differenza’ anche il numero ‘cancellato’ o ‘depennato’ (nel nostro primo esempio, b). Si usa inoltre la seguente terminologia: data la sottrazione
c – b a,
allora
c è il minuendo
b è il sottraendo
a è la differenza.
La sottrazione è dunque sicuramente ‘commutativa’ nella misura in cui è sempre legittimo permutare il ‘sottraendo’ con la ‘differenza’. Considerati, infatti, dal punto di vista dell’addizione, ‘sottraendo’ e ‘differenza’ non sono altro che ‘addendi’.
La sottrazione non è invece, se non si considerano i numeri negativi, commutativa, nella misura in cui, mentre è sempre possibile levare b (oppure a) da c, non è al contrario possibile levare c da b (oppure a), come mostra la seguente figura:
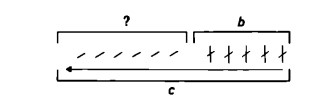
Per togliere c da b, minore di c, si dovrebbe depennare o cancellare più segni numerici di quanti ne ha b. La sottrazione b — c, dunque, ‘non va’.
A questo punto non ci interessa che tale sottrazione possa ‘in realtà’ essere eseguita. Per ora basti un semplice accenno: depennare il numero c dal numero b significa eseguire a ‘cancellazioni’, a cui non corrispondono più dei segni numerici. Tuttavia di questo discuteremo più avanti.
Un’altra osservazione: come ogni numero c può essere considerato somma di più combinazioni numeriche, a b, d + e, f g ecc., ovvero risultato di più processi di addizione, cosi ogni numero a può essere considerato differenza di coppie numeriche diverse, c — b, e — d, g— f, ecc. Per esempio, il numero 4 è la differenza di 5 e l, di 6 e 2, di 7 e 3, di 8 e 4, e così via.
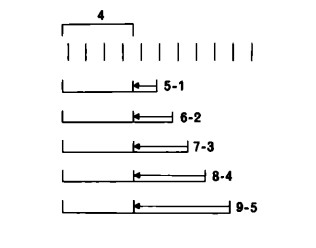
Dal momento poi che come differenza si può considerare non il resto, ma il numero sottratto (depennato, cancellato), possiamo scrivere anche
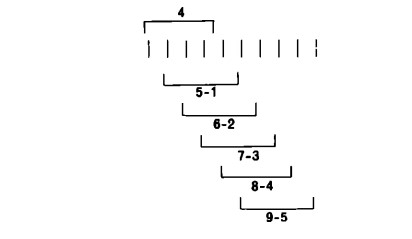
Ogni numero a è, dunque, da intendere come una ‘classe di differenze’, cioè come un insieme di infinite coppie di numeri c— b, che, sottratti in questo ordine, danno a. Così 4 è: 5 — 1, 6 — 2, 7 — 3, 8 — 4, e così via.