In questa guida spieghiamo come effettuare la sottrazione con numeri negativi.
Si prenda un numero qualsiasi a e si sottragga da esso, successivamente, prima 1, poi 2, poi 3 e cosi via, seguendo il metodo, che si è precedentemente illustrato, della cancellazione dei segni numerici a partire da destra:
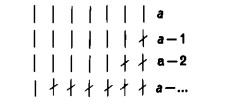
Nell’ultima sequenza abbiamo tolto tutti i segni numerici meno uno. Che cosa succede, ora, se togliamo anche l’ultimo segno numerico?
![]()
Cancellando tutti i segni numerici precedentemente scritti, ovvero cancellando esattamente a segni numerici, non abbiamo fatto altro che sottrarre a da a. Di conseguenza, possiamo esprimere la sequenza risultante con
a — a.
Per l’espressione a — a introduciamo il segno O (zero). Lo zero, dunque, è il risultato della sottrazione di un certo numero a dallo stesso numero a. Se da a si sottrae prima 1, poi 2, 3, 4, . . . , la ‘differenza’ diventa rispettivamente a, a — 1, a — 2, a — 3, a — 4, . , 3, 2, 1, 0.
Lo zero sta dunque rispetto a 1 nello stesso rapporto in cui 1 sta rispetto a 2, 2 rispetto a 3, e così di seguito. Lo zero rappresenta, per cosi dire, la prosecuzione dei nostri numeri naturali ‘verso il basso’. Leggendo da destra verso sinistra, la nostra serie diventa quindi 0, 1, 2, 3, . .
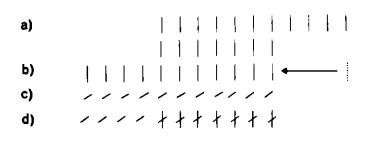
Proseguiamo, ora, nella direzione intrapresa. Quale esito può avere il tentativo di eseguire una di quelle sottrazioni che finora avevamo dichiarato ineseguibili? Vediamo. Come già sappiamo, una sottrazione è ineseguibile se il numero da sottrarre è più grande del minuendo. Si mettano ambedue i numeri uno accanto all’altro:
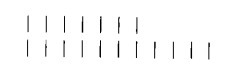
Spostiamo ora il numero maggiore in modo che la corrispondenza tra i singoli segni numerici parta da destra:
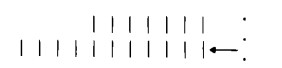
Si tenga presente, a questo punto, che ‘sottrarre’ un numero non significa scrivere dei segni numerici, ma, al contrario, cancellarli. Non possiamo perciò rappresentare il sottraendo con segni numerici, bensì dobbiamo contrassegnarlo con brevi trattini obliqui, mediante i quali simbolizzeremo il procedimento di cancellazione:
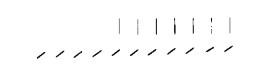
Cancelliamo dunque dal numero più piccolo dei segni numerici finché arriviamo allo zero
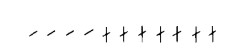
La ragione per cui la nostra sottrazione risulta ineseguibile è a questo punto ovvia: ci sono più segni di cancellazione che segni numerici; alcuni segni di cancellazione ‘avanzano’.
Compiamo ora il passo decisivo: trattiamo i segni di cancellazione come segni numerici e operiamo con essi di conseguenza.
Poiché ora il sottraendo è costituito di normali segni numerici, i nostri segni di cancellazione possono pertanto essere messi in corrispondenza biunivoca con quei segni. Ne segue che, dopo la riduzione del minuendo a zero, il numero dei segni di cancellazione che rimangono in eccedenza è esattamente uguale al numero dei segni numerici che sarebbero rimasti qualora avessimo sottratto il numero minore dal numero maggiore. Indichiamo qui di seguito i successivi passaggi:
Diciamo dunque semplicemente: i segni numerici che rimangono in eccedenza rappresentano una nuova specie di numeri — numeri che si presentano quando si sottraggono numeri più grandi da numeri più piccoli.
Visto che , poi, questi numeri risultano da un processo di cancellazione e noi abbiamo indicato questo processo di cancellazione nel campo numerico di partenza con il segno ‘meno’ (—), è del tutto ovvio chiamare questi nuovi numeri numeri negativi e contrassegnarli con il segno ‘meno’ (—) a loro anteposto.
Inoltre, poiché i segni di cancellazione si contano da destra verso sinistra allo stesso modo con cui si contano da sinistra a destra i normali segni numerici, li possiamo designare specularmente con gli stessi numerali con cui indichiamo gli altri. Questi ultimi potremo chiamarli, d’ora in poi, numeri positivi e, quando necessario, anteporre ad essi un segno ‘più’ (+), dal momento che essi vengono contati nella stessa direzione in cui si esegue il processo di addizione.
Dunque, se si sottrae un numero maggiore da un numero minore e a tal scopo si dispongono in fila da destra verso sinistra i segni di cancellazione uno di seguito all’altro, si ottengono i numeri:

Il numero col segno meno designa il totale delle cancellazioni ‘eccedenti’.
A questo punto si vede che la sottrazione è commutativa in un senso preciso. Infatti, il numero dei segni di cancellazione ‘eccedenti’ è uguale a quello dei segni numerici che rimangono quando si sottrae il numero più piccolo dal più grande. Ciò è illustrato dall’esempio:
11 — 7 = (+) 4.
7 — 11 = —4.
Ovvero, generalizzando: se c è maggiore di b.
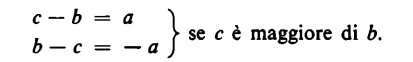
Dal punto di vista della pratica del calcolo, significa che anche le sottrazioni in cui il minuendo è minore rispetto al sottraendo sono eseguibili: basta sottrarre il numero più piccolo dal numero più grande e porre un segno meno davanti al risultato.
In questo modo lavorano anche le macchine calcolatrici che fanno sottrazioni ed addizioni. Quando si sottrae un numero più grande da un numero più piccolo, esse danno un risultato negativo (contrassegnato dal colore rosso o da un segno meno), che corrisponde in valore assoluto alla differenza che si ottiene invertendo la sottrazione.
I numeri negativi sono dunque il risultato di sottrazioni in cui il sottraendo è maggiore del minuendo e in cui si procede ‘verso sinistra’, ottenendo un”eccedenza’ di segni di cancellazione. Questo processo ha termine quando anche il numero più grande, in forma di segni di cancellazione, si è esaurito. Il numero negativo risultante corrisponde alla differenza nella normale sottrazione.
Sappiamo già che ogni numero positivo può essere considerato differenza di infinite coppie di numeri. Così, 4 è uguale a 5 — 1, 6 — 2, 7 — 3, 8 — 4, 9 — 5, ecc. Lo stesso vale anche per i numeri negativi. Otteniamo allora come risultato — 4, non soltanto sottraendo 11 da 7, ma anche eseguendo operazioni come 1 — 5, 2 — 6, 3 — 7, 4 — 8, 5 — 9, ecc.
A questo fatto abbiamo alluso nell’ultima figura lasciando intenzionalmente indeterminata l’estremità di destra dell’operazione; infatti si ottiene comunque —4, tutte le volte che la differenza in valore assoluto tra i numeri in questione è 4:
— 4 può essere uguale a:
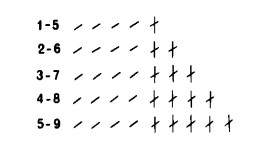
I numeri negativi sono perciò da intendere come ‘classi di differenze’, cioè come insiemi di infinite coppie di numeri che, sottratti, danno per risultato il corrispondente numero negativo.
Le riflessioni ora svolte ci suggeriscono come sia possibile rappresentare l’insieme dei numeri positivi e negativi mediante una ‘scala’ da sistemare verticalmente o orizzontalmente:
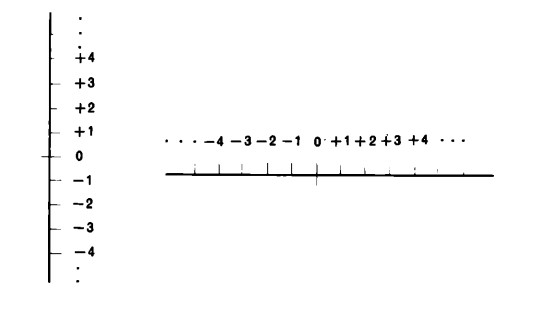
A questo punto osserviamo che i numeri negativi sono l’immagine speculare dei numeri positivi, sia per quanto riguarda i simboli numerici sia per i numerali che li designano. Questa specularità viene resa esplicita nella seguente relazione ‘quasi commutativa’:
c — b = +a
b — c = — a.
D’altra parte dobbiamo pensare che i numeri negativi sono stati escogitati per ‘estendere’ l’insieme dei numeri positivi ‘oltre lo zero’. Arriviamo, pertanto, al seguente risultato:
0 sta a + 1 nello stesso rapporto in cui + 1 sta a + 2;
—1 sta a 0 nello stesso rapporto in cui 0 sta a + 1 ;
—2 sta a —1 nello stesso rapporto in cui —1 sta a 0;
e dunque anche al seguente:
—2 sta a — 1 nello stesso rapporto in cui + 1 sta a + 2.
Questo significa che i rapporti speculari tra numeri positivi e numeri negativi non devono farci dimenticare che l’insieme dei numeri negativi e positivi è da intendere come una serie unitaria di numeri, costruita secondo un unico senso in riferimento allo spazio della nostra esperienza.
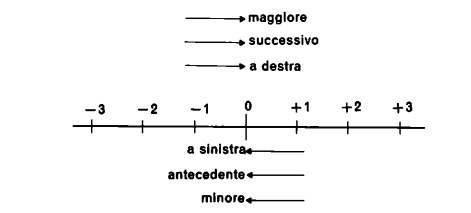
Se dunque + 2 è il successivo di + 1 e + 1 è il successivo di O, allora anche O è, nello stesso senso, successivo di — 1 e — 1 è il successivo di — 2 (e non viceversa, come potrebbe suggerire la relazione simmetrica —2 — 1 0 + 1 + 2). In ciò trova una spiegazione anche il fatto che — 1 è da considerare ‘minore’ rispetto a 0 e — 2 ‘minore’ rispetto a — 1 (e non viceversa, come potrebbe suggerire l’analogia coi numeri positivi). La rappresentazione grafica illustra quanto detto
Anche certi strumenti della vita quotidiana, come i termometri, possono aiutarci a capire il tipo di rapporto esistente tra numeri positivi e numeri negativi: la temperatura di + 1 °C è più bassa della temperatura di + 2 °C,
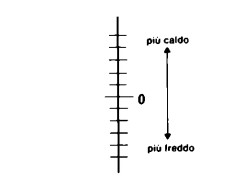
mentre la temperatura di — 1 °C è più alta della temperatura di — 2 °C.
Questo esempio ci ricorda che nella quotidianità ci sono molte occasioni che richiedono l’uso dei numeri negativi: abbiamo già visto il caso dei gradi negativi del termometro, ma ce ne sono anche altri, per esempio i saldi dei conti in dare, vale a dire i debiti, ecc. Così, chi ha 2000 euro, ma è debitore di 2500, possiede meno di niente: egli ha un ‘patrimonio’ di 2000 – 2500 = – 500 euro, ovvero un debito di 500 euro.
Deve essere chiaro comunque che la definizione dei numeri negativi non si fonda sugli esempi sopra citati, ma semplicemente sull’ampliamento del nostro calcolo con trattini, calcolo che, pur basandosi originariamente sui dati dell’esperienza quotidiana, ne è indipendente una volta che si sia iniziato il processo della numerazione.