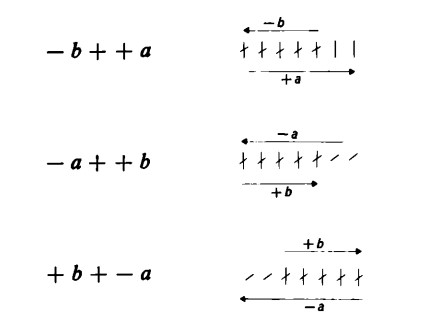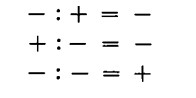In questa guida spieghiamo le operazioni con numeri negativi.
Addizione e sottrazione con i numeri negativi
Addizione e sottrazione sono operazioni opposte. Anche i numeri positivi e negativi sono numeri, in certa misura, opposti.
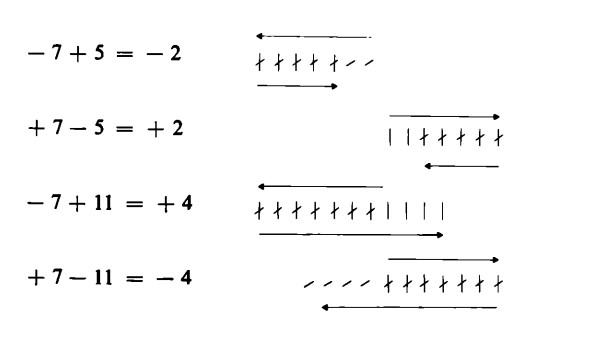
Abbiamo definito l’addizione come il processo consistente nell’aggiungere segni numerici sulla destra di una data cifra, e la sottrazione come il processo inverso, cioè il processo di cancellazione di segni numerici già scritti nella direzione opposta, ossia da destra verso sinistra. Abbiamo visto che i numeri positivi si possono pensare come figure numeriche costituite da segni numerici posti via via successivamente da sinistra verso destra. Al contrario, i numeri negativi sono il risultato di un’estensione verso sinistra della sottrazione mediante segni di cancellazione.
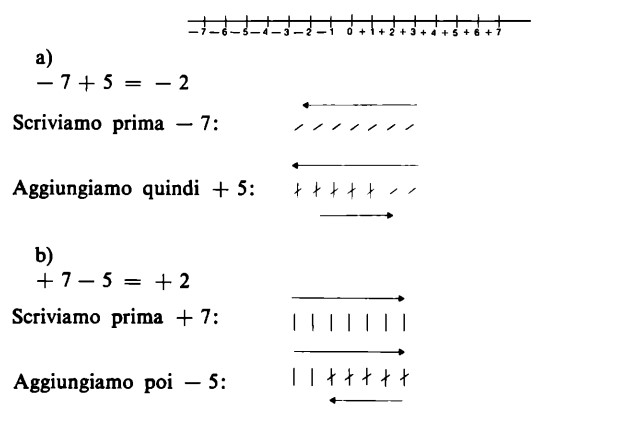
L’addizione di un numero negativo è da intendersi, pertanto, come sottrazione di un numero positivo, vale a dire come una operazione da eseguire mediante cancellazioni da destra verso sinistra. 7 + (-11) si deve perciò leggere come 7 — 11l e dà per risultato – 4.
La sottrazione di un numero negativo deve infine essere intesa, da un lato, come l’inversa dell’addizione di un numero negativo, dall’altro come l’inversa della sottrazione di un numero positivo. Siccome ambedue queste operazioni consistono nel processo di cancellazione da destra verso sinistra, la loro operazione inversa deve essere l’inverso di quelle stesse operazioni: la sottrazione di un numero negativo corrisponde, dunque, all’addizione di un numero positivo. Sottrarre -11 coincide con l’addizionare + 11. Non ha nessuna importanza se l’importo, da cui viene sottratto il numero negativo, è a sua volta positivo o negativo:
+ 7 – (- 11) = + 7 +(+ 11) = + 18;
– 7 – (- 11) = – 7 + (+ 11) = + 4.
Anche per i prossimi esempi useremo schemi costituiti da trattini e segni di cancellazione, per mettere in evidenza come anche in queste dimostrazioni non si faccia ricorso all’intuizione ottica dello spazio, ma si sfrutti il solito metodo operativo dei trattini. Gli schemi sono da interpretare in base alle seguenti convenzioni:
1) Il numero che corrisponde al primo importo (sulla sinistra) viene indicato da trattini o segni di cancellazione. La direzione e l’estensione di questo schema sono indicate dalla freccia che sta in alto.
2) Il numero che corrisponde al secondo importo (quello di destra) è rappresentato da trattini o segni di cancellazione, che, a seconda dei casi, si sovrappongono ai segni già esistenti o stanno da soli. Direzióoe ed estensione dello schema sono contrassegnate dalla freccia che si trova al di sotto dello schema a cui si riferisce.
Due esempi
Se, come in questo caso, più schemi fra loro connessi si trovano l’uno sotto l’altro, rappresentiamo questo fatto ponendo in corrispondenza verticale i ‘punti nulli’, i punti d’incontro di trattini e cancellazioni.
Per l’addizione o sottrazione di un numero negativo con un numero negativo vale quanto segue:
1) La direzione da seguire nello svolgere l’addizione, ovvero la sottrazione, rimane sempre la stessa anche nel caso in cui l’operazione inizia a partire da un numero negativo già dato.
2) Quando dunque, il primo addendo è un numero negativo, il processo dell’addizione va verso destra in direzione dello zero ovvero oltre lo zero stesso:
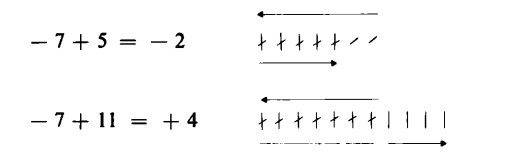
3) Il processo di sottrazione da un numero negativo va, al contrario, verso sinistra, e rimane nell’ambito dei negativi:

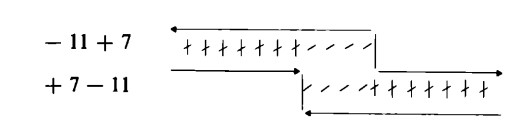
Si possono osservare delle corrispondenze speculari. L’addizione il cui primo addendo è un numero negativo corrisponde alla sottrazione il cui minuendo è un numero positivo
Viceversa, la sottrazione il cui minuendo è un numero negativo corrisponde all’addizione il cui primo addendo è un numero positivo:

Abbiamo, come s’è visto, sviluppato i numeri negativi a partire dalla sottrazione, deducendoli dai segni di cancellazione.
Per questo motivo, abbiamo definito fin da principio la sottrazione e i numeri negativi come un’operazione consistente nello ‘scrivere verso sinistra’.
Analogamente, possiamo riassumere l’addizione e i numeri positivi come un’operazione consistente nello ‘scrivere verso destra’.
In un certo senso, possiamo quindi identificare la sottrazione con la costruzione di un numero negativo e l’addizione con la costruzione di un numero positivo.
Da questo punto di vista, ogni legame (di addizione o di sottrazione) tra un numero positivo qualsiasi e uno negativo qualsiasi può essere concepito come addizione di un numero positivo e di un numero negativo, vale a dire:
a – b ovvero + a + – b,
– a + b ovvero – a + + b.
Ciascuna addizione significa: prima un certo numero di passi verso destra (sinistra), poi un certo numero di passi verso sinistra (destra). Siccome, poi, l’ordine in cui eseguiamo tali passi è indifferente
vale la seguente legge di commutatività:
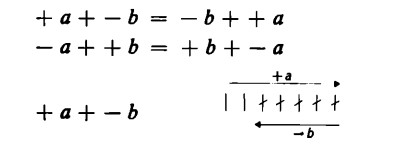
Per la sottrazione esistono dunque due tipi analoghi di commutatività: una `commutatività speculare’:
a – b = – (b – a)
(esempio: 5 – 9 = – (9 – 5) = – 4)
e una commutatività semplice:
+a + – b = – b + + a
– a + + b = + b + – a
(esempio: 5 – 9 = – 9 + 5 = – 4;
– 5 + 9 = + 9 – 5 = + 4).
È chiaro che la commutatività semplice altro non è che la commutatività dell’addizione estesa al campo dei numeri negativi.
Moltiplicazione e divisione con i numeri negativi
Che cosa succede se si dividono o si moltiplicano numeri negativi? Prendiamo un numero positivo qualsiasi a e moltiplichiamolo innanzitutto per meno uno.
Sappiamo già cosa vuol dire ‘moltiplicare per più uno’: ogni numero, preso da solo come fattore, dà come risultato lo stesso numero; esso, infatti, nello schema bidimensionale che rappresenta il prodotto, non è altro che la ‘riga superiore’.
Di conseguenza, si può dire anche che, poiché un numero moltiplicato per uno dà per risultato sé stesso, lo stesso vale quando uno è un ‘meno uno’, solo che in questo caso a si trasforma nel corrispondente negativo – a.
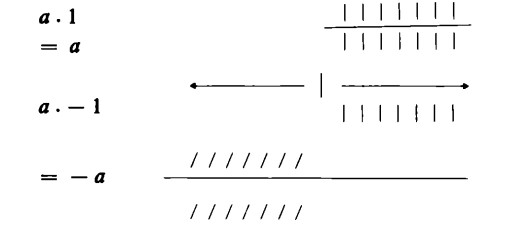
Che cosa si ottiene, ora, moltiplicando a per – b?
Siccome abbiamo posto a ⋅ -1 = – a, vale anche b ⋅ – 1 = – b e, dunque, invertendo le parti, – b = b ⋅ – 1.
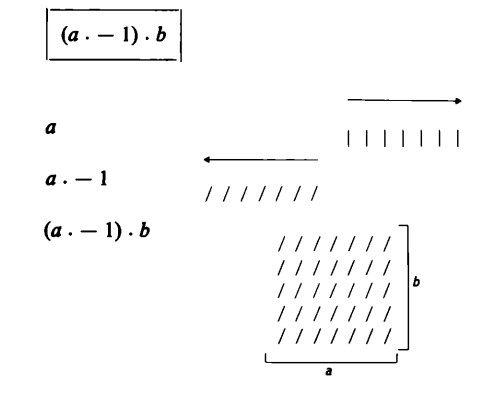
a ⋅ – b ha, pertanto, lo stesso significato di a ⋅ b ⋅ – 1.
Se ora applichiamo la legge dell’associatività della moltiplicazione, originariamente dimostrata solo per numeri positivi, a un prodotto che contiene anche il fattore negativo – 1, è possibile rendere questa espressione in tre modi diversi:
(a ⋅ – 1) ⋅ b
(b ⋅ – 1) ⋅ a
(a ⋅ b) ⋅ – 1
Abbiamo così i seguenti schemi
(scambiando il numero delle righe con quello delle colonne, ossia `ruotando’ il ‘rettangolo’)
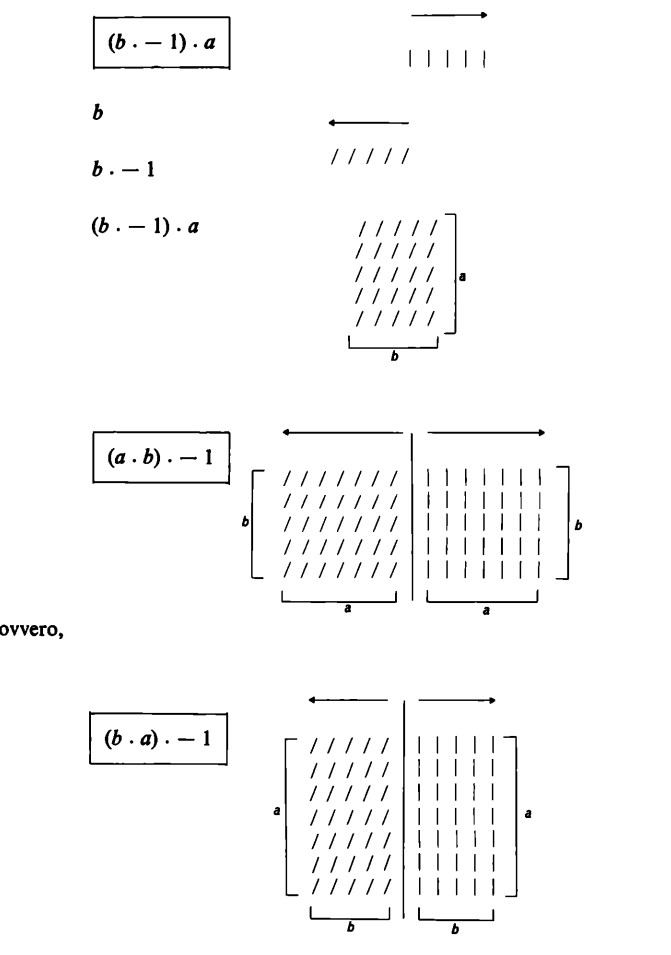
In ciascun caso si ottiene il negativo dello schema sta per a ⋅ b = b ⋅ a.
Si ha quindi:
a ⋅ – b = a ⋅ (b ⋅ -1)
= b ⋅ – a = b ⋅ (a ⋅ – 1)
= – (a ⋅ b) = (a ⋅ b) ⋅ – 1
Qual è il risultato di – a per – 1?
In base al principio che la negazione significa inversione di direzione, costruiamo innanzitutto la figura che rappresenta il numero negativo – a:
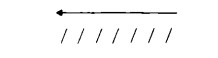
Ora, invertendo la direzione, la figura corrispondente a – a per – 1 sarà una figura con lo stesso numero di segni numerici, ma nell’ambito dei positivi:
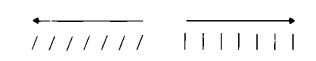
– a ⋅ – 1 dà dunque per risultato + a.
Da – a ⋅ – 1 passiamo ora a – a ⋅ – b.
Dal momento che – b = b ⋅ – 1, – a ⋅ – b ha lo stesso significato di – a ⋅ b ⋅ – 1.
Inoltre, in base a quanto già detto, – a ⋅ – 1 ha lo stesso significato di + a.
Otteniamo pertanto la seguente catena di eguaglianze:
– a ⋅ – b = – a ⋅ b ⋅ – 1 = + a ⋅ b.
Si ha quindi – a ⋅ – b = + a ⋅ b.
Il prodotto – a per – b dà allora come risultato ab, il che si esprime di solito con l’espressione: ‘meno per meno dà più’.
Molto spesso si afferma che tale regola è una pura ‘convenzione’; si sarebbe convenuto di operare tale calcolo, ma la regola in sé non avrebbe un senso.
Al contrario, le nostre riflessioni ci mostrano che questa operazione è del tutto intuitiva. Dal momento, infatti, che la moltiplicazione per – 1 si può interpretare come ‘cambiamento di direzione’ nel processo di costruzione delle figure numeriche, da ciò consegue il fatto che una doppia inversione di tale processo deve dare come risultato la direzione di partenza.
Riassumendo, i quattro tipi possibili di moltiplicazione tra numeri positivi e numeri negativi sono:
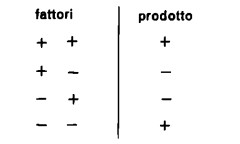
Ne deriva la seguente regola generale: segni fra loro uguali danno , segni diversi danno -.
Si osservi ancora che nel caso di prodotti ottenuti moltiplicando più di due fattori, un numero dispari di fattori negativi dà come risultato un numero negativo, un numero pari di fattori negativi dà un prodotto positivo. La ragione sta nel fatto che ogni coppia di segni meno dà come risultato un segno più.
Dalle uguaglianze
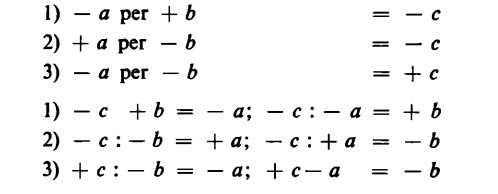
risulta immediatamente la validità della regola dei segni anche per la divisione; dalle uguaglianze sopra scritte, infatti, si ricavano le seguenti regole per segni