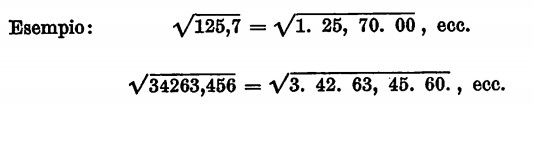In questa guida spieghiamo quali sono le proprietà delle radici e vediamo come effettuare il calcolo.
L’estrazione di radice è l’operazione inversa della elevazione a potenza. Tale operazione si indica col segno √ sul quale scriveremo in alto a sinistra il numero indicante se si tratta di una radice quadrata, cubica, ecc. Nel calcolo della radice quadrata tale numero si può anche omettere. Si dice radice di un certo indice (questo è il nome del numero scritto in alto a sinistra) di un dato numero, il numero che, elevato a quell’indice, dà il numero stesso. Infatti la radice quadrata di 4 è 2, perché 22 = 4.
Vediamo ora in pratica come si effettua l’estrazione di una radice; sia da trovare la radice quadrata di 15.215:
a) scriviamo il numero sotto il simbolo di radice
![]()
b) lo decomponiamo in gruppi di due cifre tramite puntini, incominciando da destra verso sinistra
![]()
c) cerchiamo il più grande numero che, elevato al quadrato, non superi il primo gruppo di sinistra, in questo caso 1; 1 sarà perciò anche la prima cifra della radice cercata
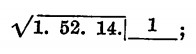
d) si eleva al quadrato il numero trovato, lo si scrive sotto il gruppo di sinistra e si esegue una sottrazione:
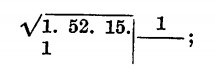
e) si abbassa il secondo gruppo separando con un puntino l’ultima cifra a destra, poi si fa il doppio della prima radice trovata, 1, e si cerca quante volte tale doppio è contenuto nella cifra avutasi come resto della sottrazione non prendendo in considerazione la cifra dopo il puntino; il risultato verrà scritto a destra del doppio della radice stessa:
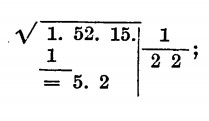
f) si moltiplica il numero trovato per il quoziente della divisione precedente: 22 • 2 = 44, risultato che viene scritto sotto il precedente (52) e da questo sottratto: 52 — 44 = 8. Si abbassa l’altro gruppo e si opera come precedentemente:
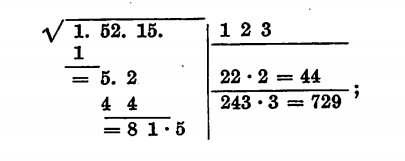
si fa cioè il doppio della radice trovata e si cerca quante volte il 24 sta nell’81; sta 3 volte (72); scriviamo ora il doppio trovato sotto la precedente moltiplicazione, separato da una linea: adesso scriviamo a destra di tale doppio il quoziente della divisione (81 : 24) e lo moltiplichiamo per il quoziente: 243 •3 = 729; scriveremo ora, a destra della radice, il quoziente, 3, e sottrarremo da 815 il risultato della moltiplicazione ricercando numeri inferiori nel caso che il prodotto lo superi. La radice potrà comunque essere approssimata per difetto o per eccesso; infatti non tutti i numeri sono dei quadrati perfetti come quelli che compaiono nelle tabelle al fondo del volume.
Se dovessimo cercare la radice quadrata di un numero come 37 (6,0828), il numero 6 sarebbe radice approssimata per difetto; il numero 7, approssimata per eccesso (36 e 49 sono i quadrati perfetti).
Qualora volessimo dare al risultato di mia estrazione di radice una maggiore approssimazione, dovremmo aggiungere due zeri al resto, separare, come di consueto, l’ultimo zero con un puntino e mettere la virgola a destra della radice e procedere poi come al solito. Una radice cosi trovata si dirà approssimata per difetto a meno di ![]()
Vi sono poi radici quadrate di numeri decimali. Si separeranno allora con un puntino le cifre a partire dalla virgola, aggiungendo a destra uno o più zeri in modo che il numero delle cifre decimali sia pari.