Già da bambini ci colpiva, rendendoci alquanto perplessi, il dilemma della velocità della tartaruga nel famoso paradosso « Achille e la tartaruga ». La cosa che però subito afferravamo in problemi analoghi era che esisteva un rapporto (la velocità, appunto) tra il cammino percorso e il tempo impiegato a percorrerlo.
Noi misuriamo la velocità in chilometri all’ora (km/h) oppure in metri al secondo (m/sec); una velocità di 3,6 chilometri all’ora corrisponde a una velocità di 1 metro al secondo.
La nostra vecchia auto impiegando 2 ore e mezzo per compiere un percorso di 90 chilometri avrà mantenuto una velocità di 36 chilometri all’ora (90 : 2,5). Questa è infatti la velocità media che però, è ovvio, non rappresenta la velocità mantenuta — istante per istante — dalla vecchia automobile.
Risulta essere illogico infatti che un veicolo purchessia assuma immediatamente la velocità di 36 chilometri all’ora e si arresti altrettanto bruscamente. Per avere la velocità vera — cioè la velocità istantanea del veicolo — occorrerà dividere il cammino percorso (ds), partendo da un determinato momento (t), in un intervallo di tempo molto piccolo (dt). A seconda del momento in cui inizieremo le nostre misurazioni, la velocità avrà valori diversi sempre però espressi dal rapporto
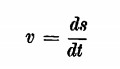
e, se il tachimetro della nostra vecchia auto indicherà a un dato momento la velocità v, il veicolo compirà un percorso dato dal prodotto v • dt.
Questo intervallo di tempo di dovrà necessariamente essere brevissimo per evitare di falsare i risultati.
Il simbolo d esprime appunto questa infinita piccolezza delle grandezze che qui sono in gioco. Se invece noi volessimo misurare in condizioni ideali, su di un’autostrada poniamo, i nostri chilometri percorsi con velocità costante, avremo un moto uniforme e diremo che quando un punto si muove con moto uniforme, tale punto compie durante un certo tempo t, il percorso dato dal prodotto vt, nel quale v rappresenta la velocità di questo punto, cioè, nel caso della nostra auto, di 36 chilometri all’ora.
Risulta essere ovvio che siamo qui di fronte a una semplificazione avendo eliminato, dalla nostra espressione, il simbolo d. Nel caso di velocità che variino arbitrariamente da istante a istante, lo scrivere il simbolo dt presuppone che in questo istante il movimento avvenga ancora in maniera uniforme.
Quale accelerazione dovrà avere ora un’automobile per raggiungere, partendo da ferma, in mezzo minuto la velocità di 72 chilometri all’ora? E quanti metri percorrerà in tale periodo di tempo?
La velocità dell’automobile, dopo mezzo minuto, corrisponde a 20 metri al secondo; poiché l’accelerazione è uguale a ![]() , avremo:
, avremo:
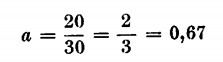
cioè metri 0,67 al secondo. Lo spazio percorso sarà dato invece da:
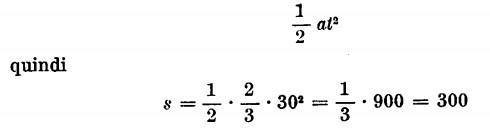
cioè lo spazio percorso dall’automobile è di 300 metri.
Immaginiamo ora che un casellante veda cadere dalla reticella di uno scompartimento ferroviario una valigia. Passando il treno davanti ai suoi occhi, egli percepisce il moto della valigia come una parabola.
Un passeggero che invece si trovasse nello scompartimento vedrebbe cadere la valigia secondo una linea retta. In sostanza la traiettoria è subordinata allo stato dell’osservatore. Dovendo definire il movimento della valigia bisognerebbe tener presente anche la sua direzione.
Una grandezza fisica è perciò definita in maniera completa o da un numero, come nel caso della temperatura, o dal dato numerico più la direzione e il verso, come nel caso della valigia che cade dalla reticella (o l’accelerazione di un’automobile). La grandezza definita dal solo numero sarà una grandezza scalare, altrimenti si dirà vettoriale.
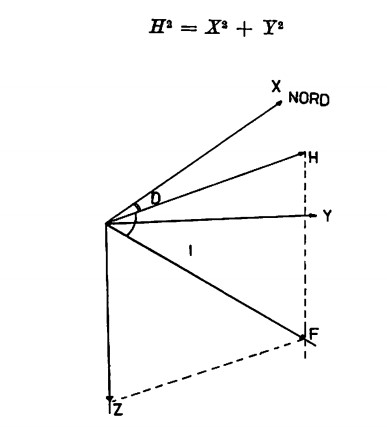
Il campo magnetico terrestre è ad esempio una grandezza vettoriale, avendo un’intensità, un verso, una direzione e lo si definirà col determinare (in valore e in segno) queste tre componenti rispetto a una prefissata terna di riferimento. In particolare potremmo scegliere il Nord geografico, l’Est e la verticale orientata verso il basso; altrimenti la componente sul piano orizzontale del punto terrestre considerato, il meridiano magnetico (direzione di un piano verticale) e la verticale orientata verso il basso.
Si avrà pertanto una relazione del tipo
nella quale H è la componente di un determinato punto nel piano orizzontale del piano magnetico, X la direzione del Nord geografico, Y la direzione Est.
Una grandezza vettoriale o vettore verrà pertanto rappresentata da un segmento orientato di lunghezza pari alla sua intensità espressa da un numero detto in fisica modulo. Qualora i segmenti siano rappresentati graficamente, occorre che la lunghezza di ciascuno di essi sia proporzionale al modulo del vettore. Se l’algebra comune serviva per le grandezze scalari, si rivela inadatta per quelle vettoriali.
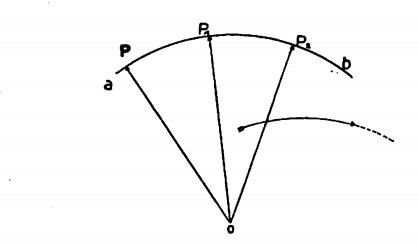
Sia la valigia che cade dalla reticella il punto P che si muove nello spazio. Se il punto P si muovesse costantemente su di un piano, si potrebbe assumere su tale piano una coppia di quegli assi cartesiani ortogonali che ci sono già serviti per i diagrammi. I valori dell’ascissa e dell’ordinata ci permetteranno di conoscere la posizione di P nei vari istanti. Se anziché su di un piano dovessimo individuare la posizione di P nello spazio, sceglieremmo tre rette perpendicolari a due a due mutualmente. Dovendo calcolare la velocità del treno, dobbiamo per forza riferirci a qualcosa di esterno al treno ovvero considerare il sistema del treno in movimento in rapporto a un sistema fisso, come potrebbe esser dato dai pali del telegrafo. Riprendiamo in esame il nostro punto P. Supponiamo che la sua traiettoria sia AB; saremo in grado di individuare la posizione di P in ogni istante per mezzo del vettore OP (O = punto fisso). In un tempo t’ il punto P è nella posizione P’, in un tempo t” nella posizione P”. Nell’intervallo di tempo (t” — t’) si ha uno spostamento di P lungo la traiettoria APB rappresentato dal vettore
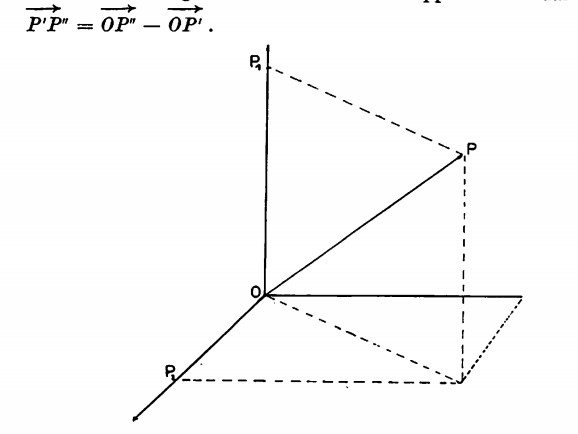
Volendo però calcolare la velocità, del treno, dobbiamo considerare che si tratta di un movimento rettilineo non uniforme.
Galileo fece interessanti studi sul moto uniformemente accelerato facendo scendere una pallina lungo un piano inclinato. Tale moto è trattato con altri argomenti nella prima giornata dei Discorsi e dimostrazioni matematiche intorno a due nuove scienze, pubblicati a Leida nel 1638 e dedicati al conte De Noailles. Gli studi sul moto accelerato erano già stati oggetto del De motu edito nel 1590 (cioè nel periodo delle esperienze del campanile pisano) e contenente le confutazioni alla teoria aristotelica, e del De motu accelerato del 1604.
Nelle esperienze galileiane veniva appunto determinato il valore di g.
La velocità è proporzionale al tempo passato dall’inizio del lancio della pallina, cioè v = gt. Facciamo cadere nel vuoto un oggetto; supponiamo che impieghi 4 secondi per compiere 160 metri. Il corpo avrà tenuto una media di 40 m/sec ( —4). La velocità non è sempre stata ovviamente la medesima, ma dallo stato di quiete si è avuto un passaggio graduale e progressivo della velocità (la velocità aumenta cioè in proporzione allo spazio percorso o al tempo trascorso).
Tornando al nostro treno, sappiamo che l’ascissa è una funzione non lineare del tempo. Dividendo la lunghezza P” —P’ per il tempo t”—t’, avremo la velocità media tra i punti P’ e P”. La velocità istantanea è data dalla derivata dell’ascissa in rapporto al tempo. Calcoliamo adesso il valore di una velocità di 60 km/h espressa in cm/sec.
Essendovi in un’ora 3600 secondi e percorrendo il treno 60 km, pari a 6.000.000 di cm, avremo:
v = 60 km/h = 6.000.000 3600 = 1667 cm/sec
Volendo esprimere in km/h la velocità di 5 m/sec, si avrà: il treno percorre 5 m/sec; quindi in 3600 sec (1 h) percorre 5 • 3600 = 18.000 m = 18 km/h. Se il treno impiegasse invece 5 ore per compiere un percorso di 300 km, è ovvio che la sua velocità media sarebbe di 60 km/h.
Riassumendo schematicamente ciò che abbiamo detto sinora, abbiamo :
a) considerato un corpo che da immobile intraprenda a muoversi con un movimento uniformemente accelerato, l’ascissa x è proporzionale al quadrato del tempo (x = kt2);
b) se P” è il punto di arrivo del corpo nel tempo t”, le ascisse dei due punti sono pertanto:
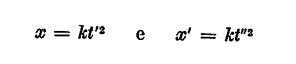
cioè nel tempo t” — t’ il corpo avrà percorso lo spazio x’ — x = = k • (t”2 — t’2);
c) velocità media:
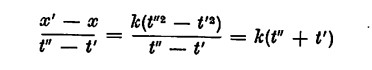
(facendo tendere t” verso t’, x’ tende verso x; velocità in un tempo t quella data dalla formula v = 2kt; la velocità istantanea = derivata dell’ascissa in rapporto al tempo);
d) accelerazione = aumento di velocità nell’unità di tempo (se v = 2k in un tempo t = 1, si ha 4k in t = 2; 6k in t = 3; ecc.).
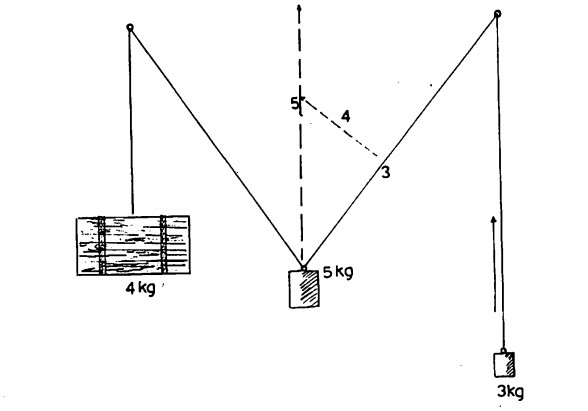
Sia ora un filo teso tra due carrucole; appesi a un capo sono 3 kg, all’altro 4 kg; sospendiamo al centro del filo un peso di 5 kg; il sistema formato dal filo e dai pesi si disporrà nella posizione di equilibrio, assumendo l’aspetto di una M, posizione che tende a riprendere se per caso noi agiamo su uno qualsiasi dei pesi.
Il peso di 5 kg lo possiamo rappresentare con un vettore lungo 5 cm diretto verso il basso. In base a ciò che è stato detto ci dovrebbe essere una forza diretta verso l’alto pure rappresentabile con un segmento di 5 cm. Sappiamo invece che una tale forza non esiste; esistono invece le tensioni dovute ai due pezzi di filo, la cui somma vettoriale equivale a questa forza equilibrante. Queste due forze si possono illustrare con due vettori orientati come il filo e lunghi 3 e 4 cm.
Al punto di congiungimento dei due vettori si origina il terzo risultante dalla somma dei precedenti, di valore 5, e cioè uguale e contrario a quello che rappresenta il peso di 5 kg. Ciò significa che in luogo di un sistema di forze applicate in un determinato punto, è lecito costituire una sola forza data pari alla somma vettoriale delle altre.
Ritornando alla pallina di Galileo e applicando ad essa un sistema di forze la cui somma sia un vettore non nullo, vedremo che la pallina stessa modifica il suo moto. Come lo modifichi dipende dal tempo di applicazione della nostra forza alla velocità iniziale della pallina.
Se indichiamo questa velocità con v, ad essa si aggiungerà un aumento dv nella direzione della forza. Applicando forze continue e variabili, obbligheremo la pallina a percorrere una parabola (si pensi al proiettile che, all’uscita della bocca da fuoco, ha una velocità v in direzione della bocca stessa, e che modifica via via la propria traiettoria a causa del peso che provoca una velocità di caduta volta verso il basso).
Sul nostro pavimento si trova un oggetto alquanto pesante. Volendolo trascinare esercitiamo su di esso una forza atta a spostarlo che si verifica nel medesimo senso dello spostamento. Il peso dell’oggetto origina delle forze normali al movimento e dirette verso il basso.
Lavoro meccanico di una determinata forza F è in fisica il prodotto F • ds (ds = spostamento nella direzione della forza). Le forze originate dal peso dell’oggetto in pratica non favoriscono e neppure ostacolano la nostra azione che invece dovrà vincere le forze d’attrito. Da ciò ne consegue che una forza la quale agisca in direzione normale ad un’altra, compie un lavoro nullo. Nel caso della forza applicata alla pallina si trattava di una forza genericamente inclinata in rapporto allo spostamento del corpo. Risultava possibile quindi immaginare lo spostamento del corpo stesso scomposto in due spostamenti parziali, uno diretto nel senso della forza e l’altro nel senso ad. essa normale (lo spostamento complessivo
somma vettoriale). Il lavoro compiuto da noi nel trascinare l’oggetto sarà dato invece dalla somma del lavoro compiuto moltiplicata, per il primo spostamento (L = F • 8). Tale lavoro viene espresso da un numero positivo se si ha il medesimo senso per lavoro e forza — concetto di trazione —, negativo se si ha senso opposto.
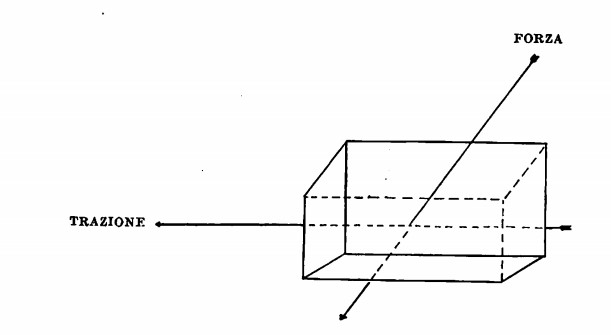
Tornando all’oggetto che trascinavamo sul pavimento diremo che un corpo compie del lavoro uscente quando questo viene espresso con un numero positivo. Il corpo subirà un lavoro entrante quando il numero è negativo. In tutti e due i casi, però, si ha uno scambio di energia da un corpo all’altro. Premendo una molla compiamo del lavoro; la Molla subisce questo lavoro, riceve dell’energia. Lasciando andare la molla questa distendendosi compie del lavoro e perde contemporaneamente l’energia acquistata. Possiamo pertanto concludere che lavoro e energia sono grandezze interscambiabili dominate dalla legge di conservazione.
È ovvio che quando un’energia non si manifesta in un lavoro non è misurabile. Quando però una macchina compie un lavoro, poniamo, di 5 kilowattora, ne perde altrettanti in energia. Volendo far proseguire la macchina nel suo moto dovremo fornirle altri 5 kilowattora…
Tendiamo un elastico; esso compirà — come la molla — del lavoro (trasformazione della energia) quando tornerà, in posizione di riposo.
La pallina di Galileo, messa in movimento, possiederà energia cinetica (proporzionale al quadrato della velocità). Se la pallina raddoppia la propria velocità l’energia diventa quattro volte maggiore. Immaginiamo ora per assurdo di veder racchiusa in una emi-sfera una centrale elettrica e che questa emisfera non lasci passare materia. Passeranno invece lavoro e energia. La somma dell’energia e del lavoro entranti Ee + Le = W (aumento d’energia all’interno della superficie stessa) = Eu Lu (energia e lavoro uscenti).
In sostanza l’energia è la capacità di compiere un lavoro; compiere un lavoro vuoi dire agire in modo che le forze producano spostamenti.
Tornando al nostro oggetto sul pavimento e supposto che il suo peso sia di 75 kg, volendo sollevarlo compiremo un lavoro di 101,5 kgm, qualora lo spostamento sia di 1,5 m.
Recandoci da un concessionario per acquistare un autoveicolo abbiamo già nella nostra mente operato una scelta in base soprattutto alla cilindrata del mezzo, e quindi al suo costo. Ma soprattutto ci ha convinti l’avere il nuovo veicolo un rapporto tra peso e potenza più favorevole del precedente da noi posseduto.
Questa fiducia nel rapporto tra peso e potenza può anche però rivelarsi di scarsa importanza agli effetti delle reali prestazioni del veicolo. In teoria infatti tale rapporto dovrebbe permettere di valutare l’accelerazione del mezzo. Esso è sempre maggiore di 1 e inferiore a 100, si esprime in kg e in cavalli. Sappiamo dalla meccanica che il prodotto della massa per l’accelerazione è uguale a forza, per cui l’accelerazione di un veicolo qualsiasi è direttamente proporzionale alla forza (agente su di esso) e, considerato che la massa è
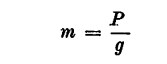
inversamente proporzionale alla sua massa.
In pratica il peso di un’automobile è quello a vuoto tenuto conto che un guidatore di peso medio, cioè circa 70 kg rappresenta il 7-8% del peso della vettura (10 q).
Quanto alla potenza possiamo sia misurarla alle ruote motrici che all’albero motore, tenendo però presente che alle ruote motrici la potenza diminuisce di circa il 6% a causa degli attriti. Quello che invece bisogna considerare attentamente nel valutare, in maniera approssimativa, la potenza della nostra automobile è anche il coefficiente di penetrazione ovvero la sua aerodinamicità.. A tale asserzione basterà il seguente esempio:
Una motocicletta convenzionale di circa 125 cc, a quattro tempi, con un buon motorino, sviluppa una potenza di circa 7,5-8 cv e pesa a vuoto circa 90 kg. Balzando in sella il peso passa di colpo dai 90 kg ai 160 sempreché il nostro peso non sia eccessivo (circa 70 kg). In questo caso la motocicletta ha un rapporto peso-potenza di circa 20 kg per cavallo. Se il guidatore se ne sta impettito come su di una poltrona, data la potenza e dato il rapporto peso-potenza (e considerando che una motocicletta di tale tipo sviluppa tale potenza a un regime di circa 5000-5500 giri minuto con una compressione all’incirca di 8 a 1) il veicolo raggiungerà in piano la velocità massima di 85 km orari.
A tale velocità si raggiunge un equilibrio tra potenza e resistenza all’avanzamento tale che ogni ulteriore aumento di velocità diventa impossibile. Tale resistenza all’avanzamento può però diminuire se il guidatore si abbassa sul serbatoio; in tal caso pur rimanendo invariati i dati di cui sopra c’è un’effettiva possibilità di maggiore accelerazione per cui si potranno raggiungere con lo stesso mezzo i 90 km/h (vento permettendo). In conclusione quindi bisogna considerare il rapporto tra la potenza alla ruota motrice e le resistenze incontrate dal veicolo.