In passato ci si divertiva con poco: un pezzo di cartone sul quale era stampata la figura di una casa a colori vivaci e sviluppata . Tanti pezzi da ritagliare e comporre insieme, incollandone le linguette laterali. Il tutto mantenuto fermo da semplici mollette da bucato.
Il piacere era però grande; la nostra figura prima posta su di un piano, prendeva a poco a poco corpo, diveniva un solido. Ed ecco il pavimento coprirsi di ritagli e gocce di colla, ma anche di casette vivaci con i bravi vasi di geranio sui davanzali. Era tutto un villaggio che ci cresceva davanti agli occhi, che disponevamo a piacere, oppure erano aerei da guerra, grossi idrovolanti, i Cant-Z, dipinti a chiazze mimetiche, o carri armati dalla torretta, ahimè, non girevole (incollata com’era sulla corazza inferiore) e che se ne stavano immobili a troneggiare sul cassettone, dato che persino i cingoli erano solo disegnati.
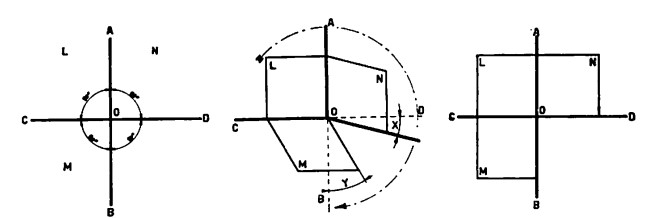
Supponiamo dunque di avere uno di quei cartoni con disegnato un dado per bambini piccoli, un bel cubetto insomma. Ritagliamolo e proviamo a piegarne i lati come segnato sulla tratteggiatura: la linea AB è una verticale che interseca la linea CD in un punto O. Questo è il punto d’incontro (centro) delle due linee.
Immaginiamo ora che queste tre facce giacciano idealmente nello spazio su di un piano verticale. La linea AB e la linea CD sono gli assi cartesiani o ortogonali e dividono il piano considerato in quattro settori di cui noi ne consideriamo soltanto tre. Questi settori, L, M, N, sono detti piani di proiezione.
Un disegno meccanico, ovvero una proiezione ortogonale e non prospettica, sarà effettuata con l’alzare il piano N dell’angolo X sulla linea CD (per avere così una linea retta e non più una linea spezzata; il piano M, spostato dalla sinistra dell’angolo Y, formerà con il piano L una continuità verticale. Il risultato non sarà altro che la proiezione (su questo piano ideale giacente nello spazio) delle tre facce del cubo prima considerato e le linee AB e CD saranno perfettamente normali fra di loro mentre il centro O sarà il luogo geometrico di un angolo giro (360 gradi).
Una dimostrazione di come raccordare geometricamente due rette convergenti fra di loro, la si può avere considerando che, tracciata la linea orizzontale e la linea verticale e prolungatele nel loro punto d’incontro, si ottiene la bisettrice dell’angolo con la semplice tracciatura del cerchio PQ puntando il compasso in O.
Puntato il compasso in P, con un’apertura PQ si è tracciato un arco di cerchio dell’ampiezza voluta. Puntando poi in Q si è ripetuta la stessa operazione. Il punto Z è trovato in tal modo. Da O e passando per il punto Z è stata poi tracciata la linea MN, ovvero la bisettrice dell’angolo formato dalle linee AB e CD convergenti. Su detta bisettrice MN il raggio formato R è il raccordo fra le due linee.
La linea AB è una verticale che interseca CD in un punto D (figura a sinistra). Queste due linee sono due assi cartesiani che dividono il piano in quattro settori; i tre settori (L, M, N) sono detti piani di proiezione. Su questi piani sviluppiamo un cubo aprendolo idealmente e facendo combaciare la retta x prolungamento ideale del lato del cubo in modo da ottenere una proiezione ortogonale e non prospettica, lo stesso si farà anche con la retta y facendola combaciare con l’asse B.