In questa guida spieghiamo quali sono le relazioni di inclusione tra gli insiemi.
Sottoinsieme e Soprainsieme
Sappiamo che ogni numero pari è un numero intero; ma non ogni numero intero è un numero pari. Numeri interi sono 1, 2, 3, 4, … , numeri pari 2, 4, 6, 8, …
Diciamo allora che l’insieme dei numeri pari è un insieme parziale o un sottoinsieme dell’insieme dei numeri interi, ovvero che l’insieme dei numeri pari è incluso in quello dei numeri interi. Il rapporto di inclusione si scrive così:
par ⊂ int
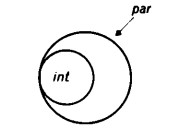
(par: insieme dei numeri pari; int: insieme dei numeri interi) e si rappresenta col seguente diagramma
In generale diciamo:
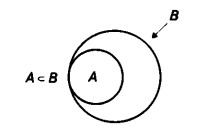
Perché, dunque, l’insieme A sia incluso nell’insieme B è essenziale che tutti gli elementi di A siano anche elementi di B; ma non è detto che valga il contrario, ossia che tutti gli elementi di B siano anche elementi di A.
Invece di dire
l’insieme A è sottoinsieme dell’insieme B,
oppure
l’insieme A è incluso nell’insieme B,
possiamo dire anche
l’insieme B è soprainsieme dell’insieme A,
oppure
l’insieme B include l’insieme A.
In matematica esistono molti esempi di inclusione tra insiemi. Vediamone alcuni: l’insieme dei quadrati è un sottoinsieme dell’insieme degli interi; inoltre gli insiemi di tutti i numeri divisibili per 3, 4, 6, 10 o per qualsiasi altro numero sono sottoinsiemi dell’insieme dei numeri naturali.
Ancora, l’insieme degli interi positivi è un sottoinsieme dell’insieme degli interi; l’insieme degli interi è un sottoinsieme dei razionali; l’insieme dei razionali è un sottoinsieme dell’insieme dei numeri reali, e così via.
Riflessività e insieme vuoto
Come già sappiamo, si può sempre dividere un numero per sé stesso e il risultato della divisione è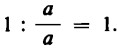 
. In maniera analoga, possiamo concepire ogni insieme come sottoinsieme di sé stesso.
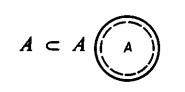
Inoltre, sempre per analogia, possiamo introdurre il concetto di ‘insieme vuoto’, come insieme che non contiene nessun elemento (ossia con zero elementi), così come a suo tempo si era introdotto nel dominio dei numeri lo zero come risultato della sottrazione di un numero da sé stesso.
Un esempio di insieme vuoto è l’insieme dei numeri dispari divisibili per 6. Infatti, siccome ogni numero divisibile per 6 deve essere pari (dal momento che lo stesso 6 è pari e i numeri pari possono avere solo multipli pari), non esistono numeri dispari divisibili per 6.
L’insieme vuoto si indica col simbolo ∅.
Insieme potenza
Dato un insieme qualsiasi, possiamo costruire tutti i suoi sottoinsiemi, vale a dire tutte le combinazioni di elementi possibili a partire dagli elementi dell’insieme originario. Diamo innanzitutto un esempio extramatematico. Una famiglia sia costituita da due genitori e da due figli; quanti possibili gruppi si possono costituire per una passeggiata, se ammettiamo che a tali gruppi possano appartenere anche tutti e quattro i membri della famiglia, con ciascun singolo membro preso da solo, e infine anche nessuno di essi?
Tale problema si può risolvere per ‘induzione completa’: cominciamo con insiemi costituiti da un solo elemento e aggiungiamo man mano un nuovo elemento, in modo da non tralasciare nessuna possibilità.
Una singola persona ha ovviamente due possibilità: può uscire o rimanere a casa.
Due persone hanno quattro possibilità: possono uscire insieme, ognuna delle due persone può uscire da sola, ambedue possono rimanere a casa.
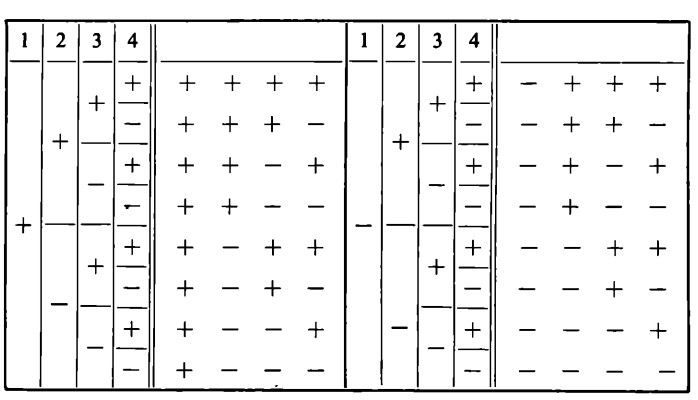
Nel caso di tre persone, possiamo applicare, senza pericolo di scorrettezza, il principio d’induzione completa, ossia il principio che ci permette di passare da un caso al successivo (da a a a + 1). Noi sappiamo infatti che per tre persone sono date tutte le possibilità che valgono per due, solo che la terza persona può aggiungersi o no a tutte le possibili combinazioni delle prime due persone: può andare, cioè, con loro o rimanere a casa. A ognuna delle quattro combinazioni delle prime due persone si aggiunge, quindi, una persona che esce insieme con le altre o rimane a casa. Se indichiamo con ‘ +’ l’uscire e con ‘ -‘ il rimanere a casa, possiamo illustrare quanto si è detto con il seguente diagramma
Se, allora, per una persona si danno due possibilità e per due persone quattro, per tre persone ci saranno 2 per 4 = 8 possibilità. Una quarta persona può di nuovo raddoppiare ognuna di queste otto possibilità con l’accompagnarsi alle altre o con il rimanere a casa, cosicché in una famiglia costituita da quattro membri esistono 16 modalità diverse di organizzare la compagnia che va in gita.
Usando le potenze, possiamo facilmente determinare che con n persone esistono 2n possibilità. Per quale motivo in questa formula compare la costante 2? Semplicemente perché abbiamo assunto due (e soltanto due) possibilità di scelta: andare in gita o rimanere in casa, presenza o assenza.
Generalizzando il caso: i sottoinsiemi di un insieme base si determinano secondo un principio dicotomico: ci si chiede soltanto se un elemento è presente o assente.
L’insieme di tutti i sottoinsiemi di un insieme (dunque l’insieme di tutte le possibili combinazioni) si chiama, per ovvi motivi, insieme potenza di quell’insieme. Se un insieme contiene n elementi, il relativo insieme potenza contiene 2n elementi (possibilità di combinazioni).
L’insieme potenza di insiemi matematici infiniti non si può evidentemente calcolare, visto che il numero n degli elementi non è fissato.