In questa guida spieghiamo unione e intersezione di insiemi.
Intersezione
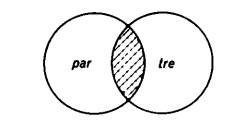
L’intersezione insiemistica ha un significato letterale ed intuitivo. Con questa parola si designa l’insieme di tutti gli elementi che appartengono contemporaneamente a due insiemi dati.
Vediamo qualche esempio. Sia dato l’insieme dei numeri pari 2, 4, 6, 8, 10, 12, … e l’insieme dei numeri divisibili per 3, cioè 3, 6, 9, 12, 15, … Evidentemente non ogni numero pari è divisibile per 3, e altrettanto si ha che non ogni numero divisibile per 3 è anche pari. Esistono tuttavia alcuni numeri che sono pari e anche divisibili per 3. Ad esempio, sono di questo tipo i numeri 6, 12, 18, 24, … (non invece 2, 4, 8, 10, … e neppure 3, 9, 15, 21, …).
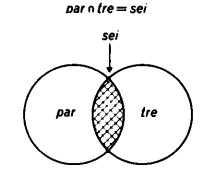
L’insieme dei numeri che sono contemporaneamente divisibili per 2 e per 3 si dice intersezione fra l’insieme dei numeri pari e quello dei numeri divisibili per 3 e si indica:
par ∩ tre.
Il seguente diagramma illustra intuitivamente il termine di ‘intersezione’:
Siccome poi l’intersezione di par e tre coincide con l’insieme dei numeri divisibili per 6 (2 per 3), possiamo anche scrivere:
È possibile costruire l’intersezione anche di altri insiemi numerici. Si può trovare, ad esempio, l’intersezione dei numeri pari e dei numeri quadrati, n altre parole l’insieme costituito dai numeri pari quadrati: 4, 16, 36, 64, 100, …
Anche in questo caso si può dare un’interpretazione matematica dell’intersezione; i numeri pari quadrati sono i quadrati dei numeri pari: (2n)2.
Unione
L’unione di insiemi è il concetto complementare dell’intersezione. L’unione di due insiemi è l’insieme che contiene tutti gli elementi appartenenti l’uno all’altro degli insiemi (anche ad ambedue gli insiemi).
Per esempio, l’unione dell’insieme dei numeri pari e di quello dei numeri divisibili per 3 è costituita da tutti i numeri pari più quelli divisibili per 3, compresi quelli che sono pari e per di più divisibili per 3.
A tale unione appartengono, pertanto, i numeri 2, 3, 4, 6, 8, 9, 10, 12, 4, 15, 16, 18.
In simboli, si scrive
par ∪ tre.
Il segno ∪ deriva dall’iniziale maiuscola U della parola ‘Unione’. Il segno ∩ per l’intersezione non ha, invece, una ragione grafica così immediata. Tuttavia, una volta che si sa che ∪ = Unione, anch’esso diventa intuitivo.
Il diagramma per l’unione insiemistica è configurato in questo modo
Dal momento che l’unione è l’insieme degli elementi appartenenti all’uno o all’altro degli insiemi in questione, non è richiesta la presenza di elementi appartenenti ad ambedue gli insiemi. Pertanto, gli insiemi di cui si vuole trovare l’unione, possono essere anche reciprocamente estranei, cioè possono non avere elementi in comune. La loro intersezione può essere l’insieme vuoto:
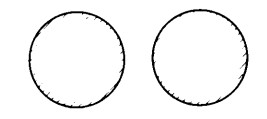
Ad esempio, l’insieme dei numeri interi è l’unione fra l’insieme dei numeri pari e quello dei numeri dispari, insiemi che non hanno alcun elemento in comune:
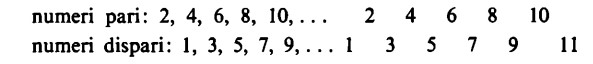
Tabelle di appartenenza
Per illustrare le varie operazioni tra insiemi, abbiamo usato, finora, delle figure piane (i diagrammi insiemistici). Tuttavia, nell’ambito della teoria degli insiemi, si possono costruire delle dimostrazioni in cui non si fa uso dei diagrammi.
Ciò è anche necessario, poiché i diagrammi, come abbiamo visto, non rappresentano correttamente gli insiemi matematici con infiniti elementi. Per questo motivo vogliamo introdurre il metodo di dimostrazione fondato sulle cosiddette ‘tabelle di appartenenza’.
Dati due insiemi A e B e una certa quantità di elementi, il rapporto tra ognuno di tali elementi e gli insiemi A e B si può configurare secondo una delle seguenti quattro possibilità:
Per ogni elemento a, esso può
-appartenere all’insieme A e all’insieme B
-appartenere all’insieme A, ma non all’insieme B;
-appartenere all’insieme B, ma non all’insieme A
-non appartenere a nessuno dei due.
Il rapporto fra un elemento e un insieme è illustrato dal diagramma
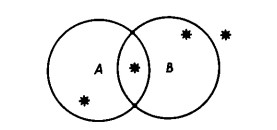
Non esiste, evidentemente, nessun’altra possibilità.
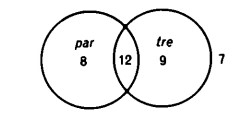
Vediamo un esempio: gli insiemi siano quello dei numeri pari e quello
lei numeri divisibili per 3.
12 è pari e divisibile per 3;
8 è pari, ma non è divisibile per 3;
9 è divisibile per 3, ma non è pari;
7 non è né pari né divisibile per 3.
Nello schema a quattro posti che si configura nel caso di due insiemi e di una certa quantità di elementi si possono far entrare tutti i numeri interi: per ogni numero si verifica una delle quattro possibilità.
La nostra tabella di appartenenza si presenta, dunque, come segue

Mediante tale tabella ci è consentito di rappresentare ogni possibile relazione sussistente tra insiemi, come è indicato nelle pagine seguenti
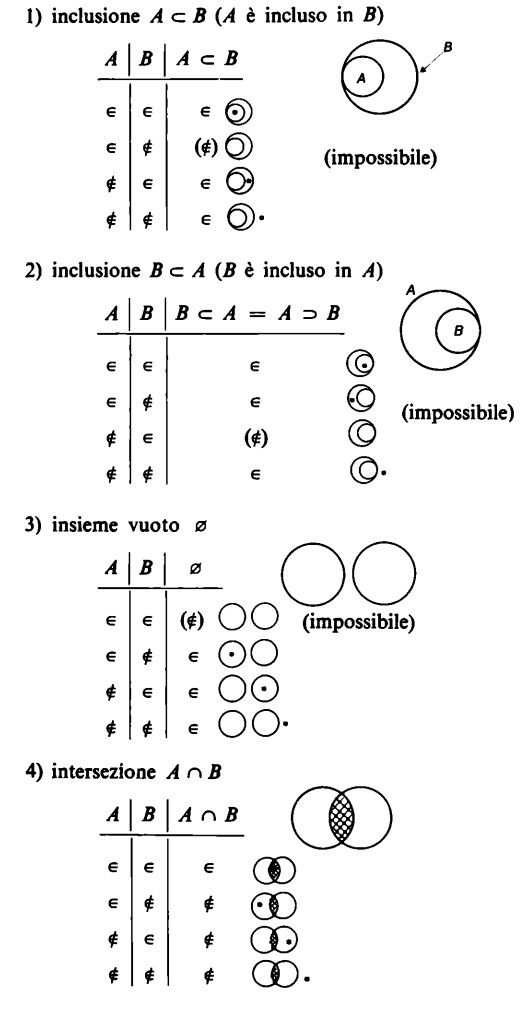
La nostra tabella mette in luce quanto segue: soltanto gli elementi appartenenti ad ambedue gli insiemi appartengono all’intersezione. Se un elemento non appartiene ad uno qualsiasi degli insiemi, non appartiene neppure all’intersezione.
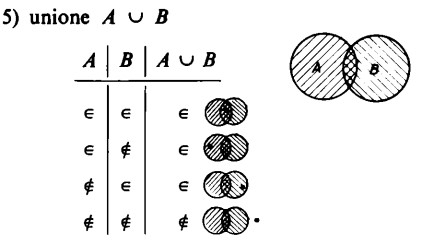
Dalla tabella risulta che all’unione appartiene ogni elemento che appartiene almeno a uno dei due insiemi. Solo gli elementi non appartenenti né all’uno né all’altro insieme non appartengono all’unione.
Ecco il motivo per cui la terza colonna della tabella per l’intersezione contiene un segno d’appartenenza e tre segni di non appartenenza, mentre la tabella per l’unione contiene tre segni di appartenenza e un segno di non appartenenza.