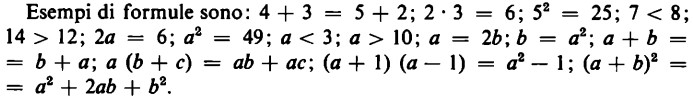Quando abbiamo introdotto il concetto di termine, abbiamo espressamente sottolineato che i termini non possono contenere segni di uguaglianza o di disuguaglianza.
Qual è il significato di tale restrizione? I termini, come abbiamo visto, sono espressioni per numeri, e precisamente per numeri qualsiasi, nella misura in cui essi contengono delle variabili, e per numeri determinati, nella misura in cui contengono costanti al posto delle variabili.
Analogamente abbiamo definito il concetto di funzione mediante il concetto di termine.
Scegliamo un numero a (l’argomento) e lo sostituiamo in un termine. Calcoliamo il valore del termine, ottenendo così il valore della funzione ƒ(a), che è a sua volta un numero. Nel definire il concetto di funzione non si parla, dunque, della relazione di uguaglianza o disuguaglianza; è anzi del tutto indifferente e accidentale il fatto che il valore della funzione sia uguale, o no, all’argomento.
Così, nella funzione a → a2, all’argomento 1 corrisponde ‘accidentalmente’ il valore 1, ad altri argomenti (come 2, 3, ecc.) corrispondono al contrario valori diversi (4, 9, ecc.).
Una funzione è dunque una semplice corrispondenza tra numeri, senza riguardo alla loro uguaglianza o disuguaglianza.
Un termine designa un numero. Nella definizione di numero non si fa riferimento a rapporti di uguaglianza o disuguaglianza. Rapporti di uguaglianza o disuguaglianza si hanno – quando in generale si hanno – soltanto tra numeri distinti.
Quando dunque un’espressione matematica contiene il segno di uguaglianza o quello di disuguglianza, in essa vengono posti a confronto due numeri distinti, e l’espressione complessiva non è più un termine.
Chiamiamo formula un’espressione matematica in cui ricorre un segno di uguaglianza o di disuguglianza.
Le formule possono contenere – esattamente come i termini – solo costanti, solo variabili oppure variabili e costanti insieme.
Formule senza variabili si chiamano anche proposizioni, formule con variabili anche forme proposizionali. In senso lato, si possono chiamare proposizioni tutte le formule; una formula e una proposizione matematica sono praticamente la stessa cosa. Le proposizioni matematiche contengono dunque segni di uguaglianza o di disuguaglianza; si potrebbe anche dire che esse sono proposizioni sulla uguaglianza o disuguaglianza tra numeri designati da termini.
Proposizioni sono dunque, ad esempio: 4 + 3 = 7; 2 per 3 = 6; 7 < 8; forme proposizionali, invece, a + b = b + a, come pure a = 2b.
Insiemi ottenuti per astrazione da formule
Le formule a > 5 e 5 < a sono soddisfatte dallo stesso dominio di numeri, cioè dai numeri che sono più grandi di 5, ovvero da quelli rispetto ai quali 5 è più piccolo.
Anche le formule a < 9 e a + 3 < 12 sono soddisfatte dallo stesso dominio di numeri; infatti, la disuguaglianza a + 3 < 12 (se aggiungo 3 ad a, ottengo un risultato minore di 12) si può trasformare nella disuguaglianza a < 9.
In ambedue i casi, si tratta dunque di una coppia di formule distinte, aventi tuttavia lo stesso valore (equivalenti) – non diversamente dai termini (a + 1) (a – 1) e a2 – 1.
Due formule equivalenti rappresentano allora lo stesso insieme.
Così, le formule a > 5 e 5 < a rappresentano l’insieme dei numeri maggiori di 5. Le formule a < 9 e a + 3 < 12 rappresentano l’insieme dei numeri minori di 9.
Negli esempi sopra illustrati ricorrevano formule provviste di una sola variabile. Si hanno, però, anche formule con due variabili, ad esempio:
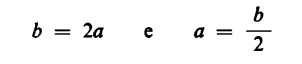
(dove a è un numero intero).
Ambedue le formule sono chiaramente equivalenti, in quanto ognuna
delle due può essere trasformata nell’altra. Un altro esempio è:
(dove a è sempre un numero intero).
Si comprende facilmente che la prima coppia di formule equivalenti designa l’insieme dei numeri che stanno tra di loro nel rapporto di un mezzo a uno (ovvero che poi è lo stesso, nel rapporto di uno a due). Siccome poi si presuppone che a sia sempre un numero intero, b sarà sempre un numero pari, ossia un numero esattamente divisibile per 2. Le formule b = 2a e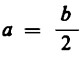 
(dove a è sempre un numero intero) rappresentano dunque l’insieme dei numeri pari.
Si può vedere in maniera del tutto analoga che la seconda coppia di formule equivalenti designa, invece, l’insieme dei numeri che stanno tra di loro nel rapporto di radice e quadrato – ove di nuovo si presuppone che i valori della radice siano sempre interi, di modo che i valori delle formule siano sempre (soltanto) dei ‘quadrati’ come 1, 4, 9, 16, 25, ecc. Le formule b = a2 e a = √b rappresentano, di conseguenza, l’insieme dei quadrati. È chiaro che per ogni formula si possono costruire infinite formule equivalenti. Ad esempio, la formula b = 2a si può esprimere, oltre che con b/2 = a anche con 2b = 4a, 3b = 6a, 4b = 8a, ecc.
Poiché tutte le formule equivalenti designano lo stesso insieme di numeri (in questo caso l’insieme di tutti i numeri pari), possiamo dire che gli insiemi si ottengono appunto per astrazione da formule.
Naturalmente, come per le funzioni, anche per gli insiemi non occorre esibire per ognuno una serie di formule equivalenti. Ad esempio, per l’insieme dei numeri pari useremo di regola la formula più semplice b = 2a e, corrispondentemente, per l’insieme dei numeri quadrati la formula b = a2. Non si deve comunque dimenticare che gli insiemi non dipendono da determinate formule, ma che diverse formule possono rappresentare lo stesso insieme in forza della loro equivalenza.
Una formula come a > 5, da cui si ottiene l’insieme dei numeri maggiori di 5, contiene una sola variabile (libera). In questo caso parliamo, dunque, di insieme `monadico’.
Le formule b = 2a e b = a2 contengono invece due variabili (libere). Per questo esse designano insiemi `diadici’, cioè gli insiemi dei numeri pari, ovvero dei quadrati.
Quando parliamo dell’insieme dei numeri pari o dei quadrati, ci troviamo di fronte a una relazione a due posti: infatti, un numero può essere un numero pari o un quadrato solo in riferimento a un altro numero intero, che ne è la ‘metà’ ovvero la ‘radice’.
Naturalmente esistono anche formule a 3, 4 e più posti, con i relativi insiemi (insiemi poliadici).
Un esempio di insieme triadico è l’insieme di tutte le ‘triple pitagoriche’, cioè l’insieme di tutti quei numeri interi a cui corrisponde la lunghezza dei lati di un triangolo rettangolo qualsiasi. Siccome per questi lati vale il rapporto a2 + b2 = c2, una tripla pitagorica non può essere costituita da tre numeri interi qualsiasi, ma soltanto da quei numeri che soddisfano la condizione a2+ b2 = c2, così come non tutti i numeri interi sono quadrati di altri numeri interi. Triple pitagoriche sono per esempio 3, 4 e 5 (poiché 9 + 16 = 25) e 5, 12 e 13 (poiché 25 + 144 = 169).
LA TEORIA DEGLI INSIEMI IN MATEMATICA E IN LOGICA
La nostra introduzione degli insiemi che si ottengono per astrazione da formule matematiche poggia sul presupposto che sia utile fare distinzione tra una teoria degli insiemi matematica ed una extramatematica. Tale distinzione non significa naturalmente che ci siano due diversi concetti di insieme, ma trova la sua motivazione nel fatto che all’interno della matematica abbiamo a che fare con insiemi del tutto diversi da quelli con cui si ha a che fare al di fuori della matematica.
Al di fuori della matematica si è soliti, talvolta, concepire gli insiemi come aggregati di oggetti privi di rapporti specifici tra di loro: così si può costruire, ad esempio, un insieme contenente un fiammifero, i! duomo di Milano, Alessandro il Grande e un utente telefonico. È ovvio che ciò non presenta alcun interesse per il concetto matematico di insieme. Naturalmente si può costituire anche l’insieme contenente i numeri 4, 11 e 15; ma qual è il senso di tale aggregato? Al di fuori della matematica si può pensare che tra questi tre numeri sussista un certo qual rapporto, per esempio che essi indichino i giorni di un certo mese nei quali è piovuto; ma all’interno della matematica ci interessano soltanto quegli insiemi, tra i cui elementi sussistano delle relazioni conformi a qualche legge matematica —come si ha nel caso dell’insieme dei quadrati.
È chiaro che, a giustificazione della teoria extramatematica degli insiemi, anche al di fuori della matematica si possono definire insiemi sulla base di determinati rapporti, ad esempio, l’insieme di tutti i cigni bianchi o di tutte le case verdi. Qui i relativi insiemi sono determinati da certe ‘proprietà’ come ‘verde’, ‘casa’, ‘bianco’, ‘cigno’.
La differenza decisiva tra insieme matematico e insieme extramatematico non sta, dunque, nella sussistenza o meno di una proprietà o formula definiente l’insieme stesso. Gli insiemi matematici sono piuttosto caratterizzati dal fatto che, essendo a disposizione una successione senza fine di numeri, essi possono contenere un numero infinito di elementi. Per elemento si intende il singolo ‘membro’ o ‘oggetto’ appartenente a un insieme.
Già in precedenza abbiamo visto che ‘infiniti’ oggetti sono pensabili soltanto nel dominio dei numeri naturali, ove `si può sempre aggiungere ancora uno’ senza limiti di sorta.
Al di fuori della matematica non si ha mai a che fare, in senso stretto, con un numero infinito di oggetti, ma soltanto con un numero imprecisato ma finito di oggetti.
Il fatto che l’insieme dei numeri naturali sia infinito porta a dei risultati paradossali che meritano di essere ricordati.
Si consideri l’insieme dei soli numeri pari. Dato un numero naturale, per grande che sia, è sempre possibile costruire un numero che sia il doppio di esso e che risulti dunque anch’esso sempre pari:
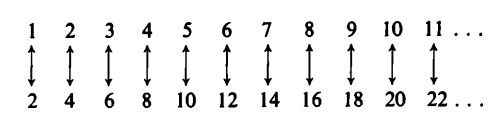
Da ciò segue il fatto paradossale che solo un numero su due è pari e, ciò nonostante, esistono altrettanti numeri pari quanti numeri naturali. Infatti, ad ogni numero si può associare un numero pari, che ne è il doppio,
Ancora più sorprendente è questo fatto se si prende in considerazione l’insieme dei quadrati. I quadrati sono infatti molto meno frequenti dei numeri pari e sono distribuiti in modo tale che più si va avanti e più aumenta la loro distanza reciproca. Ciò nonostante esistono tanti quadrati quanti sono i numeri naturali, poiché a ogni numero, per grande che sia, può essere associato il suo quadrato:
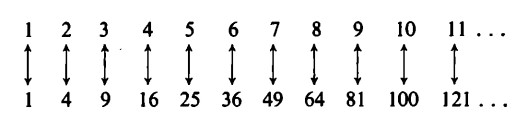
Ne segue che insiemi definiti mediante una formula possono contenere esattamente tanti elementi quanti ne sono contenuti nell’insieme dei numeri naturali, nella misura in cui la natura della formula lo consente.
Il fatto, dunque, che i numeri pari e i quadrati (lo stesso vale naturalmente anche per i numeri divisibili per 7, 19, 100 o per i numeri cubici o per altri insiemi possibili ancora) siano tanti quanti i numeri naturali, non toglie la distinzione tra numeri pari e numeri dispari e non ci deve pertanto impedire di ‘calcolare’ con quegli insiemi così come si può calcolare con insiemi finiti.
Chiariremo la possibilità di attuare questo procedimento, nella misura in cui spiegheremo le leggi generali del calcolo su insiemi esclusivamente matematici e daremo al lettore la possibilità di controllare in ogni caso la correttezza delle nostre conclusioni.
Anche in una teoria logica degli insiemi si devono trattare le stesse leggi di calcolo insiemistico (`algebra degli insiemi’), solo che nella teoria logica degli insiemi gli esempi saranno presi dalla vita quotidiana o da discipline scientifiche diverse dalla matematica.