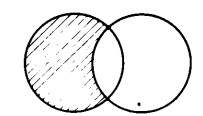
Intersezione e unione sono operazioni complementari. D’altra parte, esse hanno qualcosa in comune: tanto l’unione di due insiemi quanto l’intersezione contengono come elementi quelli che già si trovavano negli insiemi di partenza
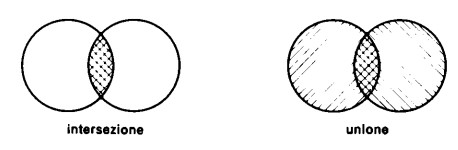
L’intersezione è costituita dai soli elementi comuni agli insiemi di partenza, mentre l’unione contiene oltre a quelli anche tutti gli elementi che appartengono all’uno o all’altro di tali insiemi.
Ciò che, invece, ancora ci manca è una composizione di insiemi sul tipo di quella illustrata in figura:
cioè l’insieme definito dall’eliminazione di certi elementi di un dato insieme.
Così come potremmo chiamare l’intersezione e l’unione con il nome comune di ‘insiemi somma’, allo stesso modo potremmo chiamare gli insiemi, da noi non ancora discussi, con il termine comune di ‘insiemi differenza’.
In seguito, chiameremo questa specie di insiemi e le relative operazioni con il termine generale di ‘insiemi differenza’.
Se dall’insieme dei numeri interi togliamo l’insieme dei numeri pari, otteniamo un ‘insieme differenza’. Questo insieme differenza è l’insieme dei numeri dispari.
Dall’insieme dei numeri pari possiamo poi estrarre tutti i numeri divisibili per 3. Rimangono tutti i numeri pari che non sono divisibili per 3, come 2, 4, 8, 10, 14, 16, 20, ecc.
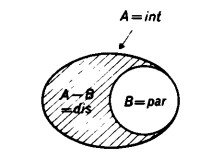
L’insieme differenza si indica mediante la formula A – B e si rappresenta graficamente così
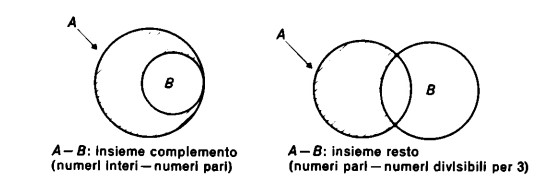
Come si vede, si possono avere in tutto due tipi di insiemi differenza.
Primo caso. L’insieme che viene sottratto, cioè B, è incluso nell’insieme da cui si sottrae, cioè A. In questo caso l’insieme sottratto coincide con l’intero insieme B.
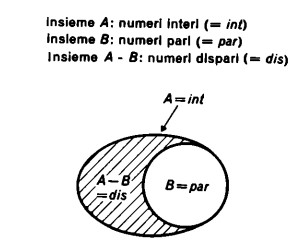
Un esempio di questo caso è che i numeri interi meno i numeri pari danno i numeri dispari (in figura, int = interi, par = pari, dís = dispari)
Visto che i numeri pari (B) sono tutti quanti compresi nell’insieme dei numeri interi (A), i numeri dispari (A – B) uniti con i numeri pari (B) danno l’insieme dei numeri interi (A). (A – B) e B sono dunque ‘complementari’ rispetto all’insieme A.
È per questo che chiamiamo A – B insieme complementare o insieme complemento di B.
L’insieme A si dice anche insieme base, poiché in esso sono contenuti tutti gli elementi (in questo caso i numeri interi) di cui si tratta.
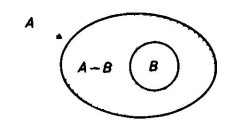
Secondo caso. L’insieme che viene sottratto, cioè B, non è incluso nell’insieme da cui si sottrae, cioè A, ma lo interseca solo parzialmente.
In questo caso, l’insieme parziale sottratto all’insieme A è un insieme parziale anche dal punto di vista dell’insieme B.
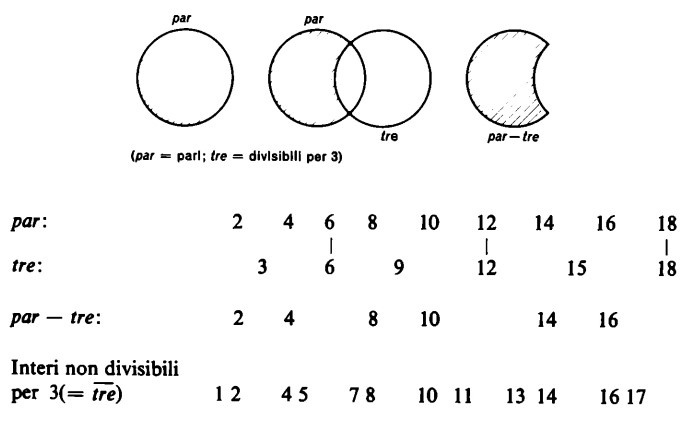
Un esempio è il seguente: i numeri pari meno i numeri (pari) divisibili per 3 sono i numeri pari non divisibili per 3.
A=numeri pari
B= numeri divisibili per 3
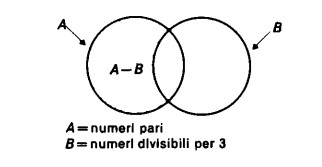
Visto che i numeri divisibili per 3 (B) non sono tutti quanti contenuti nell’insieme dei numeri pari (A), i numeri pari non divisibili per 3 (A – B) e i numeri divisibili per 3 (B) non sono `complementari’ rispetto ad A. Infatti, in B si trovano anche numeri dispari divisibili per 3, ma questi sono fuori considerazione, in quanto A contiene solo numeri pari.
A – B si chiama in questo caso insieme resto rispetto ad A.
A non è poi, in tale caso, l’insieme base, dal momento che in B si trovano anche elementi che non appartengono ad A (precisamente i numeri dispari divisibili per 3).
Insieme complemento
Per costruire un insieme complemento si parte dunque dall’insieme base A, nel quale si trova interamente incluso l’insieme da sottrarre B. L’insieme che si ottiene mediante sottrazione di B da A è l’insieme complemento A – B, insieme che unito a B dà nuovamente l’insieme A.
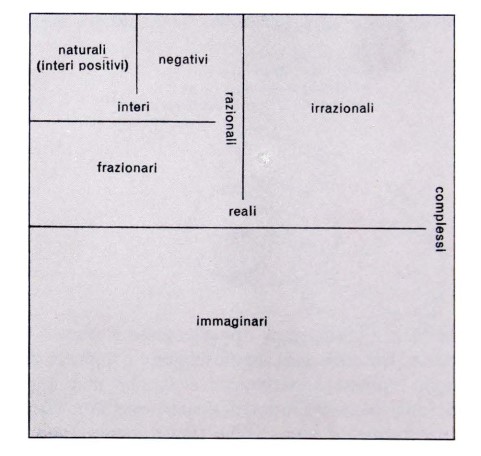
In questo senso sono insiemi complementari: l’insieme degli interi positivi e quello degli interi negativi, la cui unione coincide con l’insieme base degli interi; l’insieme degli interi e quello dei numeri frazionari, la cui unione coincide con l’insieme dei numeri razionali; l’insieme dei numeri razionali e quello dei numeri irrazionali, la cui unione coincide con l’insieme dei numeri reali.
Infatti: i numeri interi meno i numeri negativi sono i numeri positivi; i numeri razionali meno i numeri interi sono i numeri frazionari, e così via.
Già da questo esempio si vede come il concetto di soprainsieme sia un concetto relativo, dipendente dagli insiemi che si vogliono porre a confronto.
Il soprainsieme degli interi positivi e degli interi negativi, ossia l’insieme degli interi, è un sottoinsieme all’interno della coppia complementare `numeri interi / numeri frazionari’ la cui unione coincide con l’insieme dei numeri razionali.
L’insieme dei numeri razionali è di nuovo — con il suo complemento, cioè l’insieme dei numeri irrazionali — un sottoinsieme dei numeri reali
A – B e B sono insiemi complementari.
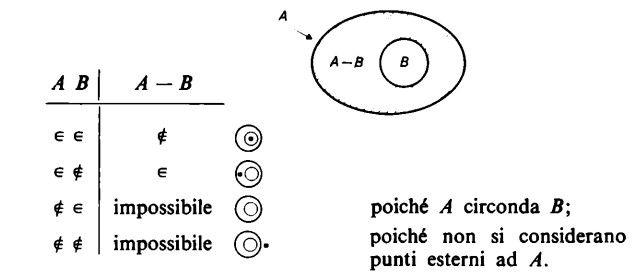
Ambedue i casi in cui un elemento non appartiene ad A non possono essere discussi, in quanto non può essere preso in considerazione nessun elemento situato al di fuori di A.
La terza riga porta a una contraddizione, dal momento che B è incluso in A, cioè tutti gli elementi che appartengono a B devono appartenere anche ad A.
La quarta riga non porta a una contraddizione, dal momento che gli elementi in questione si possono pensare collocati al di fuori di A e, pertanto, anche di B. Ma proprio perché questi elementi sono situati ‘al di fuori’, non sono oggetto di discussione. Vediamo un esempio
1. All’insieme A e all’insieme B appartengono i numeri pari.
2. All’insieme A, ma non a B, appartengono i numeri dispari.
3. Non esistono numeri appartenenti a B, che non appartengono ad A; infatti, non sono pensabili numeri dispari che non siano interi.
4. Esistono naturalmente numeri che non appartengono né all’insieme A né all’insieme B, e questi sono i numeri che non sono né interi né pari, cioè tutti i numeri frazionari, irrazionali e immaginari. Qui non si ha contraddizione: infatti, i numeri citati possono non essere pari, dal momento che non sono interi. Tuttavia in questo contesto sono fuori considerazione.
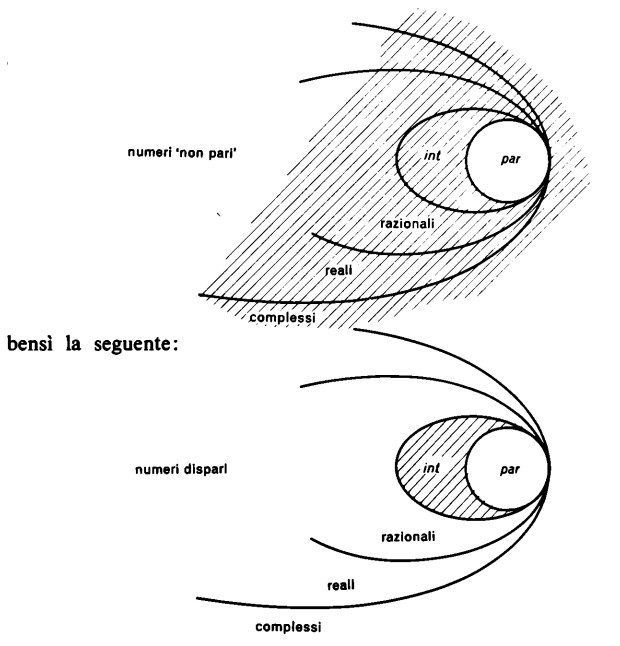
Ancora una osservazione. Il termine numero ‘dispari’, nel senso etimologico di numero ‘non pari’, si riferisce, letteralmente, anche a tutti i numeri non interi (numeri frazionari, irrazionali e complessi). Ciò nonostante, a
nessuno verrà in mente di chiamare, ad esempio, il numero 1/3 numero ‘dispari’, dal momento che esso è ‘non pari’. Se è vero, infatti, che per numero dispari si intende un numero non pari, è pur vero che con tale espressione non si vuol designare un numero non pari qualsiasi, bensì sempre un numero intero, anche se non lo si dichiara esplicitamente. La configurazione del campo numerico non è dunque la seguente
Per le notazioni si osservi che l’insieme complemento si indica molto spesso con un trattino orizzontale da sovrapporre al simbolo dell’insieme.
Insieme resto
Il concetto di insieme complemento ha senso, dunque, solo se l’insieme che si sottrae è un insieme parziale dell’insieme di partenza A.
Se, al contrario, il dominio dell’insieme B sottratto è più vasto del dominio dell’insieme A, si parla solo di ‘insieme resto’ nel dominio di A.
Se, ad esempio, togliamo dall’insieme dei numeri pari l’insieme dei numeri pari divisibili per 3, allora l’insieme resto dei numeri pari non divisibili per 3 non è naturalmente l’insieme complemento dell’insieme di tutti i numeri interi divisibili per 3, ma l’insieme complemento dei soli numeri pari divisibili per 3.
La tabella di appartenenza che rappresenta l’insieme resto è la seguente
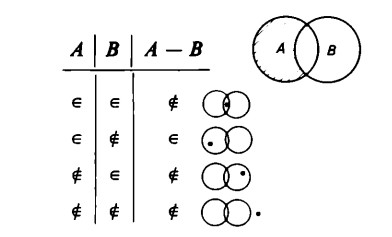
Elementi dell’insieme resto sono per l’appunto quegli elementi che appartengono ad A, ma non a B.
Calcolo con insiemi differenza
Discutiamo ora le regole di calcolo per insiemi differenza. Si vedono subito notare forti divergenze rispetto alle regole relative agli insiemi somma.
Idempotenza, insieme vuoto, commutatività, distributività
Con gli insiemi differenza non vale innanzitutto la legge dell’idempotenza, vale a dire la legge secondo la quale un insieme collegato con sé stesso dà il medesimo insieme. Così, l’intersezione di A con A era A e, parimenti, era A l’unione di A con A
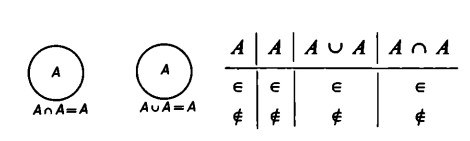
Al contrario, la differenza A- A darà come risultato l’insieme vuoto
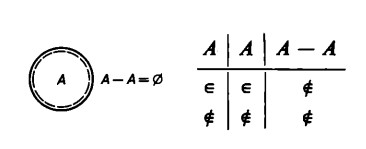
Se dall’insieme dei numeri pari togliamo l’insieme dei numeri pari, non ci rimane nessun elemento. Non vale neppure la commutatività
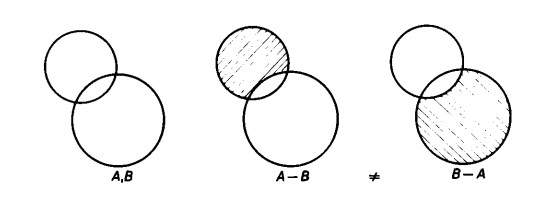
A – B e B – A danno come risultato delle figure completamente diverse, in quanto gli elementi che si ottengono dopo le rispettive sottrazioni non sono gli stessi.
Se, ad esempio, si sottrae dall’insieme dei numeri pari quello dei numeri divisibili per 3, si ottengono i numeri 2, 4, 8, 10, 14, 16, 20, . . .
Se, al contrario, si estrae dall’insieme dei numeri divisibili per 3 quello dei numeri pari, rimangono i numeri 3, 9, 15, 21, …
La tabella corrispondente alle due precedenti operazioni è la seguente
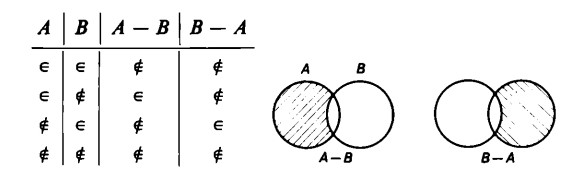
Come è facile verificare, le colonne dei valori finali sono diverse.
A questo punto, potremmo vedere se le operazioni relative agli insiemi differenza godono della proprietà distributiva. A tale scopo, oltre alla differenza, avremmo bisogno ancora di un’altra forma di composizione insiemistica, l’intersezione o l’unione. I risultati sarebbero interessanti, ma, a questo punto, ci porterebbero troppo lontano.
Somma booleana
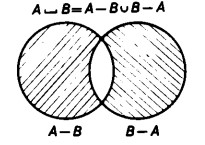
La somma booleana è, in un certo senso, l’inverso dell’intersezione. Dati due insiemi A e B, essa si ottiene unendo l’insieme differenza A – B con l’insieme differenza reciproco B – A. Dunque, in contrapposizione con l’unione, la somma booleana contiene solo quegli elementi che appartengono all’uno o all’altro degli insiemi di partenza, ma non ad ambedue.
Per esempio, la somma booleana dei numeri pari e dei numeri divisibili per 3, verrebbe a contenere i numeri
2, 3, 4, 8, 9, 10, 14, 15, 16, . . .
ma non conterrebbe, d’altra parte, i numeri
6, 12, 18, …
La tabella della somma booleana è la seguente:
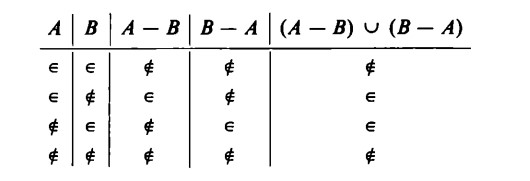
Alla somma booleana di A e B appartengono, dunque, solo gli elementi appartenenti ad A o a B, ma non ad ambedue.