Le operazioni insiemistiche dell’intersezione e dell’unione si comportano analogamente alle operazioni numeriche dell’addizione e della moltiplicazione; ciò si vede anche a proposito delle proprietà di cui godono, come la commutatività, l’associatività e la distributività.
Commutatività
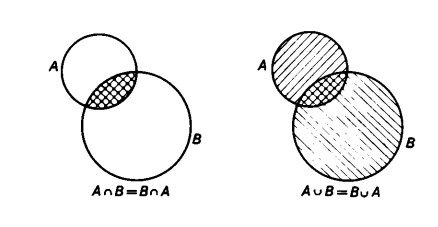
L’intersezione e l’unione di insiemi godono della proprietà commutativa:
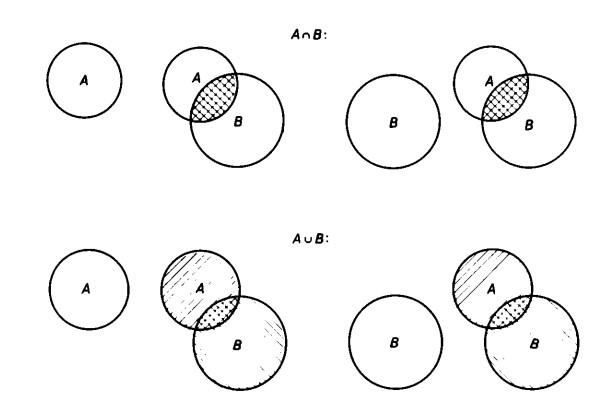
La dimostrazione di tale proprietà si può ricavare immediatamente da un semplice esame della figura stessa.
È indifferente segnare prima l’insieme A e poi intersecarlo con B (ovvero unirlo con B) oppure segnare prima l’insieme B e poi intersecarlo con A (oppure unirlo con A)
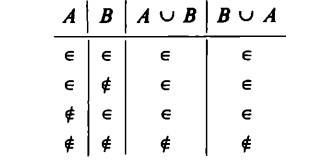
La commutatività dell’intersezione e dell’unione si può dimostrare anche col metodo delle tabelle
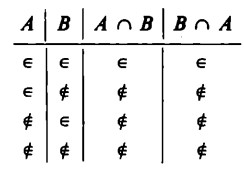
Il segno di appartenenza ∈ compare nelle colonne dei risultati solo se esso compare sia sotto A sia sotto B.
In ambedue le colonne di A ∩ B e B ∩ A si trova la medesima successione di segni d’appartenenza o non appartenenza. Gli insiemi che si ottengono in ambedue i casi contengono, quindi, gli stessi elementi.
Lo stesso risultato si ottiene analogamente anche per l’unione. Qui il segno d’appartenenza ∈ compare nelle colonne finali solo se compare sotto A
o sotto B, quindi quando compare almeno una volta nelle prime due colonne della tabella
Associatività
Le operazioni numeriche dell’addizione e della moltiplicazione godevano della proprietà associativa e distributiva. Dobbiamo dire lo stesso anche della intersezione e dell’unione?
Per rispondere a tale domanda abbiamo bisogno di tre insiemi A, B e C, in quanto le proprietà di cui si tratta richiedono un gioco di rapporti più complesso rispetto a quello che si può ottenere prendendo in considerazione due soli insiemi.
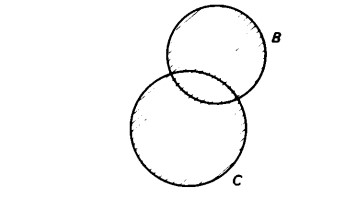
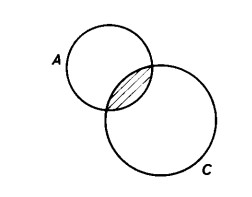
Vediamo prima se l’intersezione è associativa, se cioè è indifferente intersecare prima A con B
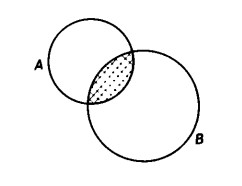
e intersecare successivamente questa intersezione con C, oppure intersecare prima B con C
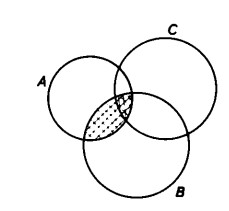
e intersecare successivamente questa intersezione con A ;
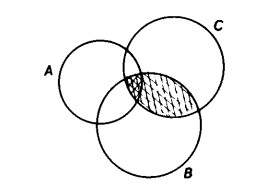
vale a dire se si ha:
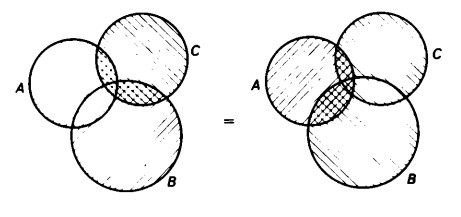
Il diagramma ci mostra che ambedue i procedimenti sono equivalenti, in quanto si ottiene sempre la stessa figura, cioè un cuneo nella zona delle intersezioni dei tre insiemi. L’intersezione è pertanto associativa.
Con tre insiemi, il numero delle righe corrispondenti alle combinazioni a cui possono dar luogo, in una tabella, il segno di appartenenza e quello di non appartenenza, sale a otto. Con due insiemi avevamo infatti quattro possibilità. Queste possibilità si raddoppiano con tre insiemi, dal momento che per ogni combinazione può darsi che l’elemento appartenga a C o non vi appartenga:
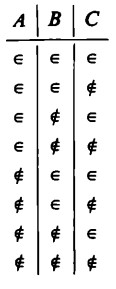
Ogni due righe si hanno qui le quattro precedenti possibilità valide per A e B soltanto, possibilità che nella terza colonna si suddividono ancora, di volta in volta, in due casi.
Il computo avviene secondo lo schema a noi noto:
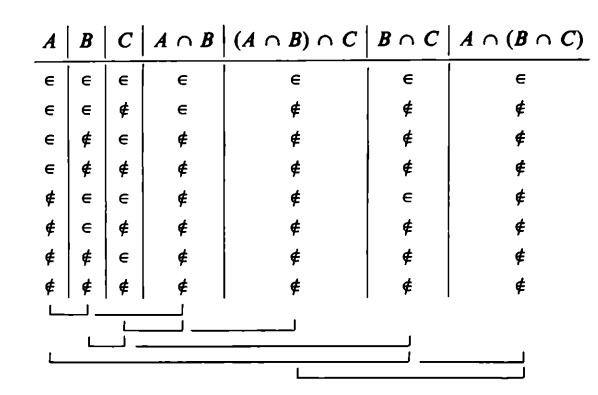
Nella tabella precedente non esistono colonne uguali, solo le due colonne finali coincidono. Per motivi di chiarezza abbiamo graffato, in calce alla figura, le colonne che sono contemporaneamente interessate al calcolo.
Nell’eseguire tale calcolo abbiamo applicato in ogni passaggio la regola dell’intersezione, secondo la quale il segno di appartenenza ∈ può comparire nella colonna finale solo se esso compare in ambedue le colonne di partenza. Nelle colonne corrispondenti a 
compare la stessa successione di segni di appartenenza e di non appartenenza (precisamente un ∈ e sette ∉). Il fatto che tali due colonne coincidano dimostra la validità della proprietà associativa per l’intersezione. In altri termini:
Qualunque sia l’ordine in cui si intersecano i tre insiemi, si ottiene cioè sempre lo stesso risultato.
In modo analogo si può mostrare che anche l’unione gode della proprietà associativa:
Utilizzando i diagrammi, risultano le due figure equivalenti che seguono
In ogni caso, come si vede, risulta la medesima superficie complessiva. Lasciamo al lettore il compito di dimostrare questo stesso risultato con il metodo delle tabelle.
Distributività
Le leggi distributive per gli insiemi corrispondono nella loro forma a quelle dei numeri.
Sappiamo che per l’addizione e la moltiplicazione vale la legge distributiva:
a (b + c) = ab + ac.
Ad essa corrisponde una legge distributiva anche per gli insiemi
La legge insiemistica si presenta, dunque, anche graficamente identica a quella numerica; l’unica differenza è che al posto di + compare ∪ e al posto della per compare ∩.
In parole essa si può formulare così:
`l’insieme A intersecato con l’unione di B e C è uguale all’unione delle intersezioni di A con B e di A con C’.
Per analizzare i rapporti di distributività dobbiamo perciò combinare l’operazione dell’intersezione con quella dell’unione.
Di tale combinazione vogliamo analizzare innanzitutto alcuni semplici casi e prepararci così alle considerazioni più complesse che seguiranno.
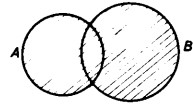
Poniamo perciò in rilievo l’unione di A e B, tratteggiando dal basso verso l’alto e da sinistra a destra la superficie corrispondente
e intersechiamo tale unione con A, ricoprendo quest’ultimo con un tratteggio in senso contrario
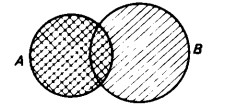
La superficie dell’intersezione è quella tratteggiata nei due sensi. Essa copre l’intera superficie corrispondente all’insieme A. Si ricava immediatamente dalla figura la relazione:
A ∩ (A ∪ B) = A.
Un esempio ne è l’unione dei numeri pari con i numeri divisibili per 3:
2, 3, 4, 6, 8, 9, 10, 12, 14, 15, 16, . ..
intersecata con i numeri pari:
2, 4, 6, 8, 10, 12, 14, 16, …
Ne risulta evidentemente l’insieme dei numeri pari.
Applichiamo ora il metodo delle tabelle.
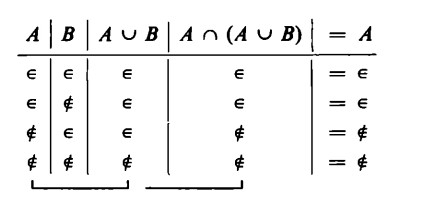
Qual è il senso di tale tabella?
Anzitutto si scrive la successione di valori corrispondenti a A ∪ B. Dopodiché si costruisce l’intersezione di A e A ∪ B. A tale scopo, basta analizzare le colonne di A e di A ∪ B e confrontare i valori che si trovano riga per riga nell’una e nell’altra.
Per la definizione di intersezione, nella colonna finale compare il segno ∈ solo se in ambedue le colonne di partenza compare lo stesso segno ∈. Basta che ∉ compaia una sola volta perché anche nella colonna finale si debba mettere il segno ∉.
Per questo stesso motivo ambedue le righe superiori danno come risultato ∈, la terza ∉ (a causa di ∉ e ∈) e la quarta ancora (a causa di ∉ e ∉).
La successione di valori ∈ ∈ ∉ ∉ che si trova nella colonna finale corrispondente a (A ∪ B) ∩ A è identica, però, alla colonna che si trova sotto l’insieme A e ciò ha il seguente significato: ogni elemento che appartiene all’insieme (A ∪ B) ∩ A appartiene anche all’insieme A, ogni elemento che non appartiene all’insieme (A ∪ B) ∩ A non appartiene neppure all’insieme A.
Un discorso analogo si può fare anche per la seguente proposizione: A unito con l’intersezione di A e B dà come risultato A.
Si indichi A tratteggiando la figura corrispondente in senso trasversale da sinistra a destra e dal basso in alto.
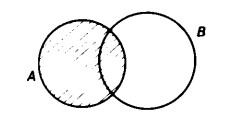
Ora, si inserisca nella figura l’intersezione A ∩ B tratteggiata nella direzione contraria
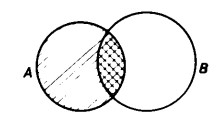
Siccome l’intersezione A ∩ B non può oltrepassare l’estensione di A, anche l’unione di A con A ∩ B si deve trovare dentro l’estensione di A. Usando il metodo delle tabelle, si ha:
Questa volta dobbiamo confrontare fra loro i valori corrispondenti alle colonne di A ∩ B e A; otterremo perciò ogni volta ∈, ∉ se almeno una colonna contiene e, e solamente se ambedue le colonne contengono ∉.
Possiamo ora passare alla dimostrazione della vera e propria legge distributiva.
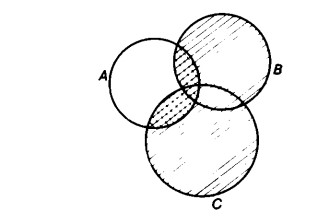
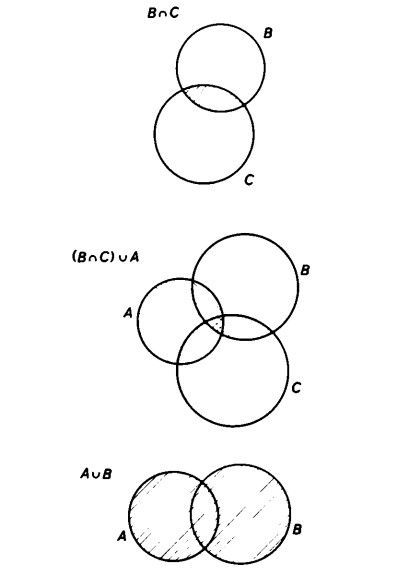
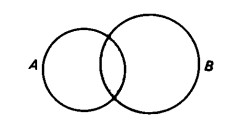
Innanzitutto costruiamo il diagramma corrispondente all’unione B ∪ C
e lo intersechiamo con A
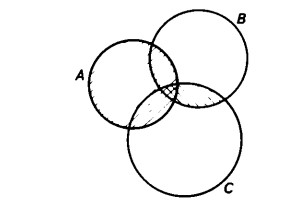
Costruiamo ora il diagramma dell’intersezione A ∩ B
e quello dell’intersezione A ∩ C
Uniamo tutte e due le figure ottenute in precedenza
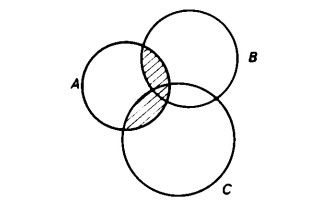
In ambedue i casi si ottiene la stessa figura avente forma di due lenti,
che corrisponde all’uguaglianza
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C).
Veniamo ora al metodo delle tabelle
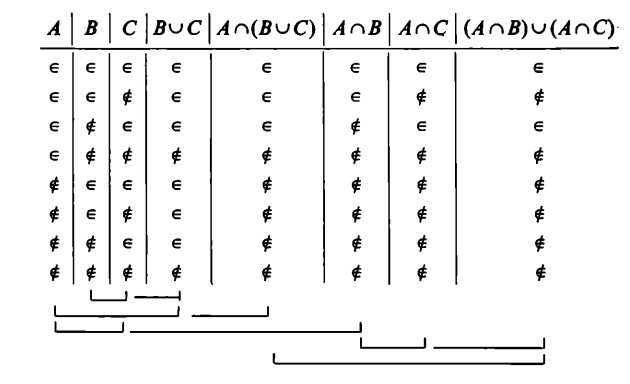
Anche in questo caso le graffe ci facilitano il lavoro. Questa volta dobbiamo fare attenzione ai casi in cui è da applicare la regola per l’unione e a quelli in cui è da applicare invece la regola per l’intersezione.
Contrariamente a quanto accade nella teoria dei numeri, nell’algebra degli insiemi vale anche la legge distributiva inversa
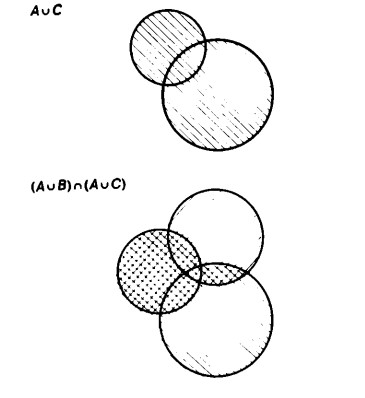
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪C),
che significa: l’insieme A unito con l’intersezione di B e C dà come risultato l’intersezione delle unioni di A con B e di A con C.
In forma di diagrammi si ha:
In ambedue i casi si ottiene la medesima figura, cioè un cerchio più un `pezzo di lente’.
Lasciamo al lettore la dimostrazione dello stesso risultato con il metodo delle tabelle.