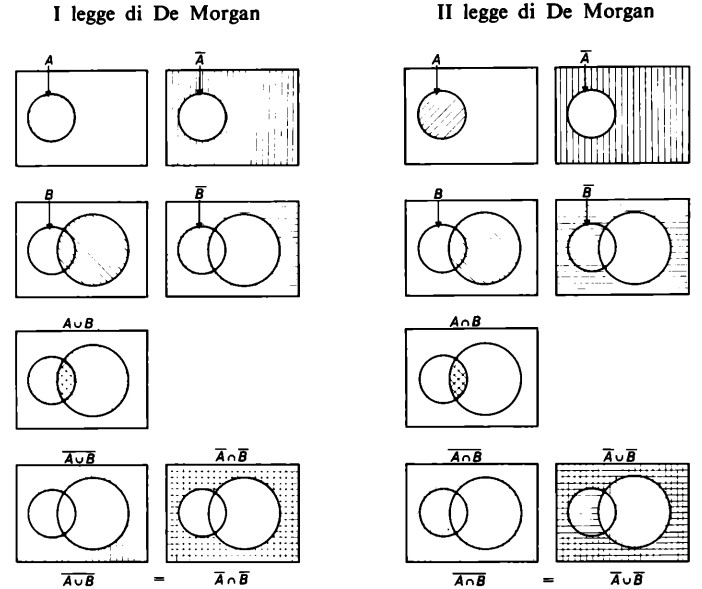
Per gli insiemi complementari sono importanti le due leggi di De Morgan.
Esse concernono le operazioni dell’unione e dell’intersezione, applicate a insiemi complementari. Si possono formulare nella maniera seguente:
l’insieme complemento dell’unione degli insiemi A e B è l’intersezione degli insiemi complementari e
l’insieme complemento dell’intersezione degli insiemi A e B è l’unione degli insiemi complementari.
In simboli (soprassegnando col trattino l’insieme complemento), si ha
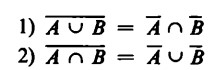
Illustriamo ora, nei vari passaggi, le leggi testé enunciate con i diagrammi
Lo specchietto è tuttavia alquanto complesso e necessita perciò di qualche spiegazione.
Qui si tratta esclusivamente di rapporti tra insiemi complementari. Questi ultimi sono da pensare situati nell’involucro’rettangolare della figura, mentre i ‘buchi’ all’interno rappresentano gli insiemi A e B, che vengono `estratti’ dall’insieme base.
Per trovare il complemento dell’unione di A e B, basta, quindi, costruire l’unione A ∪ B e poi ‘estrarla’ dall’insieme base. All’interno della figura viene ovviamente a crearsi un ‘buco’ a forma di otto, corrispondente all’insieme unione. Questo ‘otto’ si può tuttavia interpretare anche come intersezione degli insiemi complementari di A e B, che, presi singolarmente, danno un rettangolo con un ‘foro’ in forma di A ovvero di B. Siccome poi l’intersezione di due insiemi si presenta graficamente come quella zona, nella quale i due insiemi che si intersecano si sovrappongono, i due insiemi complementari si intersecano nella zona situata all’esterno di A e B, e questo è lo spazio che corrisponde precisamente al complemento dell’unione di A e B.
In maniera analoga si può costruire il complemento dell’intersezione di A e B; basta costruire l’intersezione A ∩ B e poi sottrarla dall’insieme base. Visto che l’intersezione di A e B è solo quella piccola zona nella quale A e B si intersecano, il complemento di questa intersezione è una grande massa con un ‘foro’ molto piccolo a forma di lente. Tale intersezione `a forma di lente’ si può, però, interpretare anche come unione degli insiemi complementari di A e B, che danno un rettangolo con un buco in forma di A, ovvero di B. Siccome poi l’unione di due insiemi ha un’estensione almeno pari a quella di ognuno di tali insiemi, l’unione degli insiemi complementari di A e B coprirà non solo lo spazio esterno ai ‘fori’ A e B, ma anche quello interno dove l’uno non viene intersecato dall’altro (A ovvero B). La zona in cui gli insiemi A e B si intersecano corrisponde a un foro a forma di lente, che nessuno degli insiemi complementari riesce a coprire; esso non può pertanto far parte dell’unione dei complementi.
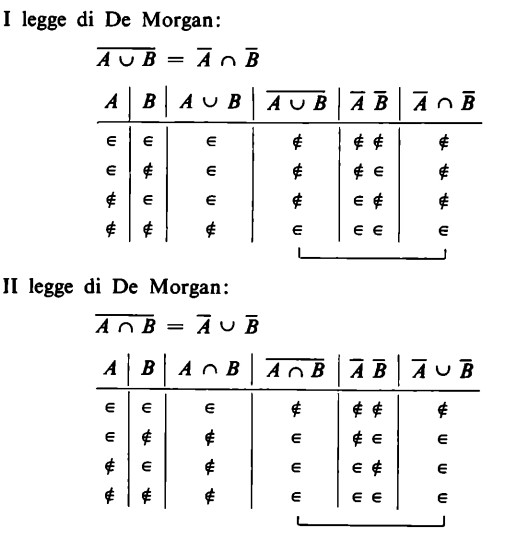
Questo si spiega facilmente col metodo delle tabelle
Le tabelle hanno la seguente spiegazione. Si trova innanzitutto l’unione, ovvero l’intersezione, in base alla tavola che già conosciamo. Poi si costruisce il complemento, scambiando il segno ∈ con il segno ∉.
Sempre attraverso Io scambio di ∈ con ∉ costruiamo i complementi 
e 
Troviamo quindi i valori corrispondenti in base alle normali tabelle dell’intersezione e dell’unione.
Abbiamo così dato l’idea delle più importanti leggi della teoria degli insiemi, ovvero dei più importanti teoremi dell’algebra degli insiemi. L’algebra degli insiemi da noi trattata vale sia per insiemi matematici sia per insiemi non matematici. Noi ci siamo comunque sempre riferiti a insiemi matematici.
La teoria logica degli insiemi ha come oggetto gli stessi teoremi, in riferimento solo a esempi non matematici. Inoltre, avendo a che fare con operazioni tipiche della logica, la teoria logica degli insiemi getta un ponte tra logica e algebra degli insiemi.
In questo libro tuttavia non possiamo occuparci di ciò, proprio per il fatto che abbiamo sin qui cercato di sviluppare la matematica senza far riferimento alla logica. A tal fine avremmo dovuto operare con idee e relazioni, che avrebbero richiesto una spiegazione di carattere prettamente logico.