Risulta essere possibile occupare lo spazio della retta numerica con numeri razionali fra loro sempre più fitti: tra due qualsiasi, che si trovano arbitrariamente vicini l’uno all’altro, è infatti possibile inserirne, tramite successivo ampliamento delle frazioni, uno nuovo e proseguire poi allo stesso modo indefinitamente.
Ci chiediamo, ora, se è possibile ottenere in questo modo ‘tutti’ i numeri `esistenti’.
I numeri razionali, per quanto complicati possano essere, hanno una proprietà in comune: essi sono dei ‘numeri frazionari’, si possono cioè esprimere mediante due numeri interi, dei quali uno sta al numeratore e l’altro al denominatore. Possiamo con ciò concludere di aver compreso nella retta numerica tutti i numeri ‘possibili in linea di principio’ (ove per `possibili in linea di principio’ si intende: costruibili all’interno dell’insieme potenzialmente infinito dei numeri)?
Dobbiamo a questo punto riflettere sulle circostanze che ci hanno di volta in volta condotto alla costruzione dei nostri nuovi numeri.
Già per due volte, fino a questo momento, si è presentato il caso che lo svolgimento di un’operazione fondamentale del calcolo, che si poteva eseguire senza delimitazioni in una direzione, non sempre era realizzabile nella direzione contraria.
Abbiamo perciò introdotto un nuovo dominio numerico per rendere eseguibili senza delimitazioni anche le operazioni contrarie. Con tale accorgimento, la sottrazione senza delimitazioni ci portò al concetto di numero negativo e, quindi, di numero intero, mentre, a sua volta, la divisione senza delimitazioni ci portò al concetto di numero frazionario, e quindi di numero razionale.
Sappiamo tuttavia che esistono altre operazioni inverse. Infatti, allo stesso modo che la moltiplicazione è addizione di addendi uguali, così anche l’operazione dell’elevazione a potenza non è altro che la moltiplicazione ripetuta dello stesso fattore.
Di conseguenza, allo stesso modo che la sottrazione è l’operazione inversa dell’addizione e la divisione quella della moltiplicazione, anche l’elevazione a potenza ha la sua corrispettiva operazione inversa — in realtà ne ha, per l’esattezza, due, a causa della sua manifesta asimmetria: l’estrazione di radice e il logaritmo.
Anche qui salta chiaramente agli occhi l’eseguibilità non illimitata delle operazioni inverse.
È possibile infatti costruire il quadrato di ciascun numero naturale:
Ma i quadrati sono distribuiti in modo assai rado e gli intervalli diventano sempre più grandi. Possiamo ricavare con facilità la radice quadrata di 1, 4, 9, 16, 25, 36, …; ma qual è la radice quadrata di 2, 10, 39? Quale numero moltiplicato per sé stesso dà come risultato uno di quei numeri?
In maniera analoga possiamo costruire le ‘potenze di 2’, vale a dire i numeri nei quali il 2 non compare, come nei quadrati, in quanto esponente, in quanto cioè numero che indica quante volte una base deve essere moltiplicata per sé stessa, ma, al contrario, in quanto base, ossia in quanto fattore da moltiplicare più volte per sé stesso. Si ottengono, così, i numeri che hanno origine raddoppiando progressivamente il numero e i numeri che ne risultano:
Dalla precedente tabella si può facilmente vedere che l’esponente del numero 32, espresso sotto forma di potenza in base 2, è 5. Ma qual è l’esponente da dare ai numeri 3, 10 o 47, se anche questi ultimi vengono intesi come potenze di 2, cioè se vengono espressi nella forma 2n?
Ora, l’introduzione dei numeri razionali ci può essere di aiuto nella soluzione di tale problema. Infatti mediante i razionali l’intervallo compreso fra due numeri interi si può riempire in modo arbitrariamente fitto. La radice di 1 è 1, la radice di 4 è 2. Di conseguenza la radice di 2 deve essere un numero compreso tra 1 e 2; tale numero inoltre dovrebbe essere un numero razionale, da poter esprimere mediante una frazione, cioè una coppia di numeri interi.
Purtroppo la radice di 2 non è uno dei numeri razionali finora a noi noti; in altri termini, la radice di 2 non si può esprimere mediante una frazione, ossia una coppia di numeri interi.
In matematica si è soliti dimostrare tale fatto per mezzo di un procedimento ‘indiretto’, usato molto volentieri anche in altri settori della scienza. Cioè: per dimostrare una data cosa, si fa vedere che la sua negazione porta ad una contraddizione.
Nel nostro caso: cominciamo col supporre che la radice di 2 sia un numero razionale. Tale ipotesi ci fa, in seguito, cadere in contraddizione e da ciò si ricava che la radice di 2 non può essere affatto un numero razionale.
Se la radice di 2 fosse un numero razionale, essa si potrebbe scrivere sotto forma di frazione:
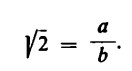
Allora, elevando al quadrato ambedue i membri della uguaglianza, si otterrebbe:
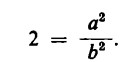
Supponiamo ora che la frazione 
sia già ‘semplificata’ al massimo. Qualsiasi frazione si può semplificare al massimo; ciò si verifica qualora il numeratore e il denominatore non hanno più fattori in comune. Per esempio, la frazione 
, nella quale il numeratore e il denominatore hanno in comune il fattore 2, si può semplificare nella frazione 
; 3 e 4 sono ‘primi tra loro’.
Dunque, anche la frazione si può ‘semplificare al massimo’, e ciò a prescindere da come essa si presenta ‘all’inizio’.
Siccome due numeri primi tra di loro non hanno divisori comuni (eccetto 1), essi non si possono dividere neppure per 2. Pertanto essi non possono essere ambedue pari; almeno uno dei due deve essere dispari. Ciò vale anche per a e b.
Il quadrato di un numero pari è sempre un numero pari, mentre il quadrato di un numero dispari è sempre un numero dispari, come mostrano le seguenti formule: un numero pari si può indicare con l’espressione 2 X n, un numero dispari con l’espressione 2 x n + 1. Se ora eleviamo al quadrato ambedue le espressioni, otteniamo:
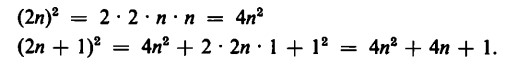
Il primo quadrato è un numero pari, il secondo invece un numero dispari.
Ne segue che, non solo dei numeri a e b, ma anche dei loro quadrati a2 e b2 almeno uno deve essere dispari.
Ora, però,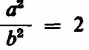 
e perciò a2 = 2b2. Di conseguenza a2 sarebbe divisibile per 2; in altri termini, a2 sarebbe un numero pari. Ma allora, siccome almeno uno dei due numeri deve essere dispari, dovrebbe esserlo b. In conclusione, se a fosse pari, b sarebbe dispari.
Se però a fosse un numero pari, il suo quadrato dovrebbe essere divisibile per 4, come s’è visto sopra nel ricavare il quadrato dei numeri pari 2 quello dei numeri dispari (ogni numero pari contiene infatti il fattore 2 e questo fattore deve essere elevato anch’esso al quadrato, poiché (m n)2 = m2n2). Ma la metà di un numero che è divisibile per 4 deve essere divisibile per 2, dal momento che 4 è 2 per 2.
Dal momento allora che a2 = 2b2, b2 è la metà di a2. Ma b2 non può a sua volta essere pari, dovendo essere nello stesso tempo il quadrato di un numero dispari.
Se dunque esistesse un numero razionale che fosse radice di 2, b sarebbe contemporaneamente pari e dispari. Questa è una contraddizione e con ciò è dimostrato che la radice di 2 non può essere un numero razionale.
Dimostrazioni analoghe si potrebbero trovare anche per altri numeri naturali – la dimostrazione sarebbe solamente un po’ più complicata. È comunque decisivo il fatto di aver dimostrato, almeno per una radice quadrata, quella di 2, che essa non è un numero razionale – che cioè devono esserci altri numeri, diversi da quelli razionali.
Che d’altra parte debba esistere un numero corrispondente alla radice quadrata di 2, risulta dalla seguente semplice costruzione grafica. Si disegni un quadrato con lato di lunghezza pari a l e si tracci la diagonale
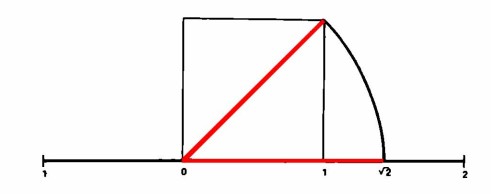
Dal momento che, per il teorema di Pitagora, il quadrato costruito sula diagonale è equivalente alla somma dei quadrati costruiti su due lati,
Il quadrato costruito sulla diagonale è pari a 12 + 12 = 1 + 1 = 2; di conseguenza, la lunghezza della diagonale risulta pari alla radice quadrata di 2, utilizzando appunto come unità di misura la lunghezza del lato. Un valore approssimativo per la radice di 2 si otterrebbe, pertanto, misurando nella maniera più esatta possibile la suddetta diagonale.
Si può giungere a valori approssimati anche facendo dei calcoli. Basta infatti trovare quel numero che, moltiplicato per sé stesso, dà come risultato ‘circa’ 2. Dal momento che 1 è la radice di 1 e 2 la radice di 4, la radice di 2 deve trovarsi tra 1 e 2.
Siccome poi 14 per 14 = 196 e, analogamente, 1,4 per 1,4 = 1,96, 1,4 è già un buon valore approssimato per la radice di 2. Giunti a questo punto, possiamo procedere oltre nel calcolo di valori sempre più approssimati: possiamo calcolare alternativamente valori `approssimati per eccesso’ e valori `approssimati per difetto’ e, in tal modo, avvicinarci sempre più al valore esatto. Non è il caso di eseguire tale serie di operazioni. Si può, comunque, trovare che la radice quadrata di 2 è un numero decimale le cui cifre iniziali sono 1,4142…
Sappiamo già che cosa è una frazione decimale. Abbiamo detto che ogni numero razionale si può rappresentare come una frazione decimale finita o come una infinita, ma periodica.
Un numero non razionale come la radice di 2 non può dunque corrispondere a una frazione decimale finita oppure infinita periodica, ma corrisponderà a una frazione decimale infinita ‘non periodica’; si tratterà di un numero decimale `irregolare’, nel quale emergono, per cosi dire, cifre decimali sempre nuove e `imprevedibili’.
Non possiamo approfondire ulteriormente il problema dei numeri non razionali. Vogliamo aggiungere solo quanto serve per concludere.
Già i numeri razionali, come abbiamo visto, si trovano distribuiti `con compattezza’ lungo la retta numerica, poiché fra due numeri razionali qualsiasi è sempre possibile inserirne uno nuovo. Ciò nonostante possiamo porre ‘tra’ i numeri razionali ancora quanti numeri non razionali vogliamo. Che esistano almeno altrettanti numeri non razionali che razionali, segue logicamente già dal fatto che tutte le somme e i prodotti tra numeri razionali e non razionali sono non razionali.
Anche tale risultato si può ottenere ragionando per assurdo: supponiamo che x sia un numero non razionale, per esempio √2 e ad esso si sommi o con esso si moltiplichi il numero razionale a. Se ora il risultato di tali operazioni fosse un numero razionale r, si avrebbe x + a = r e xa = r. Ne seguirebbe però che x = r – a e, rispettivamente,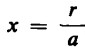 
, con x dovrebbe essere un numero razionale.
Esistono però dei numeri non razionali che si possono costruire ‘direttamente’, come √3, √5, ecc.
In quanto punti della retta numerica, i numeri razionali e non razionali devono giacere ‘compatti’ l’uno accanto all’altro. In forza di tale rappresentazione grafica, la totalità dei razionali e dei non razionali si chiama il `continuo’. I numeri non razionali li chiamiamo anche ‘irrazionali’.
Quando non ci si vuole compromettere con l’immagine spaziale richiamata dalla parola ‘continuo’, si è soliti definire il complesso dei numeri razionali e irrazionali con il termine generico di numeri ‘reali’.
I numeri reali sono dunque tutti quei numeri che si possono immaginare situati sulla retta numerica. Così, si può trovare facilmente sulla retta numerica l’immagine di √2. Basta costruire su tale retta un quadrato di lato 1 e ruotare la diagonale del quadrato sulla retta
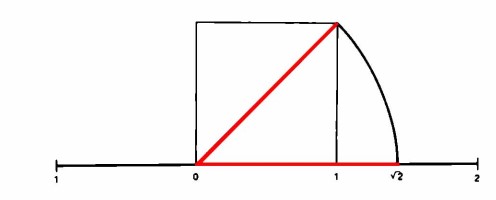
Oltre alle radici quadrate esistono molti altri tipi di numeri irrazionali. Possono essere irrazionali, per esempio, le radici cubiche o le radici di indice ancora superiore: inoltre sono irrazionali gli esponenti da dare a determinate basi per ottenere determinati numeri. Si rammenti il concetto di logaritmo: 22 = 4 e 23 = 8, allora log2 4 = 2 e log2 8 = 3. Il logaritmo in base 2 del numero 6, cioè l’esponente da dare al numero 2 per ottenere il numero 6, è un numero irrazionale compreso tra 2 e 3.
Un numero irrazionale è anche π, cioè quel numero che indica quante volte la circonferenza di un cerchio è maggiore del diametro. Anch’esso si può rappresentare spazialmente: basta disegnare un cerchio di diametro 1, svolgerne la circonferenza e portarla a contatto della retta
