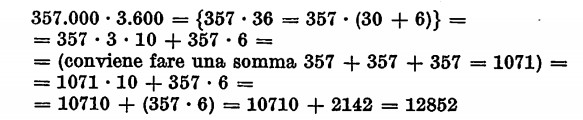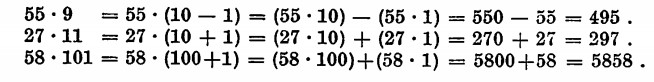In questa guida spieghiamo quali sono le proprietà delle moltiplicazioni e vediamo come eseguire il calcolo.
Si sommino i seguenti addendi: 4, 4, 4, 4; la loro somma sarà 16.
Invece di scrivere tutta la somma scriviamo più brevemente 4 • 4 = 16. Il puntino (può essere anche il segno di x) si può leggere moltiplicato per o molto più semplicemente per. Il puntino risulta molto più pratico soprattutto in algebra, dove è evidente la possibilità che il segno x (per) venga scambiato con una x (ics). Nella moltiplicazione testé osservata si chiamerà il primo numero moltiplicando e il secondo, cioè quello che ci indica quanti sono gli addendi, moltiplicatore. Diremo, in via più generale, che il prodotto di due numeri non rappresenta altro che la somma di tanti addendi uguali al primo in numero pari alle unità indicate dal secondo, e, sempre per rimanere nel campo della regola astratta, diremo che la moltiplicazione è l’operazione con la quale, dati due numeri, se ne trova il prodotto. Vi sono alcuni casi particolari della moltiplicazione che vanno attentamente esaminati:
a) qualsiasi numero moltiplicato per zero dà come risultato zero (34 • = 0);
b) qualsiasi numero moltiplicato per uno resta invariato (34 • 1 = 34) dal che si suole dire che il numero 1 è, per la moltiplicazione, un numero indifferente;
c) qualsiasi numero moltiplicato per dieci o una potenza di dieci (100, 1000, 10.000, 100.000, ecc.) aumenta di tanti zeri quanti sono quelli contenuti nel moltiplicatore. Nel caso invece di numeri decimali, si sposterà verso destra la virgola di tanti posti quanti sono gli stessi zeri.
Possiamo anche dare una raffigurazione geometrica della moltiplicazione. Osserviamo un rettangolo; la sua base moltiplicata per l’altezza ci dà l’area. Per raffigurarci geometricamente l’area di un rettangolo possiamo immaginare questo stesso rettangolo diviso in tanti piccoli quadrati, ciascuno rappresentante un’unità. Pensiamo infatti a un rettangolo che abbia la base di 3 m e l’altezza di 2 m. La sua area sarà data dal prodotto 3 • 2 = 6; possiamo perciò immaginarlo diviso da 6 quadrati ciascuno di 1 m di lato. Risulta quindi che il prodotto di due numeri è l’area di un rettangolo che ha come dimensioni i due stessi numeri.
Anche la moltiplicazione ha le sue proprietà. La proprietà commutativa ci dice che il prodotto non cambia se cambiamo l’ordine dei fattori.
La proprietà associativa ci dice che il prodotto di più fattori non cambia se al posto di due (o più di due) di essi sostituiamo il loro prodotto eseguito in precedenza e che ha nome di prodotto parziale.
La proprietà dissociativa invece ci dice che, al posto di un qualsiasi fattore se ne possono sostituire due o più ìl cui prodotto dia quello stesso fattore.
La proprietà distributiva invece ci dice che, dovendo moltiplicare un numero per una somma o per una differenza, possiamo moltiplicare questo stesso numero per ciascuno dei termini della somma o della differenza eseguendo poi la stessa somma o differenza dei prodotti ottenuti.
Una proprietà che ci sarà utilissima in algebra è il cosiddetto raccoglimento a fattor comune, il quale non è altro che l’inverso, della proprietà distributiva e ci permette, in una somma o differenza tra prodotti, di raccogliere l’eventuale fattore comune ai vari termini. Questo raccogliere lo si indica anche come mettere in evidenza. Facciamo un esempio strano.
Immaginate che giungano nel cortile di una cascina tre (o più) autocarri carichi di sacchi. Questi autocarri sono siglati rispettivamente A, B, C, e recano tutti il medesimo carico di grano. I sacchi di grano possiamo indicarli con la lettera x.
Dovendo conoscere il quantitativo dei sacchi potremo scrivere: A x + Bx + Cx oppure x(A + B + C). L’esempio, anche se non è esattamente calzante, può servire a spiegare però il perché
25 +15 = 5(5 + 3) = 5 • 8 = 40 .
Un’altra proprietà della moltiplicazione ci dice che, volendo moltiplicare per un numero un prodotto indicato, si può moltiplicare per quel numero ognuno dei singoli fattori.
Vediamo ora in pratica tutte queste proprietà.
Vi sono certamente dei limiti alla loro applicazione se si sconfina dal campo dei puri numeri a quello delle misure agricole per non parlare di scienze come la chimica.
Una cosa infatti è innestare un nespolo su una pianta di mele cotogne e un’altra cosa è fare il contrario: dalla prima operazione si ottiene un bel frutto, dalla seconda nulla. Queste proprietà però ci sono invece utilissime per il calcolo mentale rapido, per avere cioè forme ultra veloci di moltiplicazione.
Dovendo eseguire un prodotto come 28 • 5, si penserà al prodotto di (20 + 8) • 5 = 100 + 40 = 140.
si aggiungeranno ora tanti zeri quanti ne avevano i due numeri (5). Il numero finale sarà così 1.285.200.000.
Moltiplicazioni rapide
Vediamo alcuni esempi di moltiplicazioni riferiti a riprova del metodo di calcolo mentale rapido
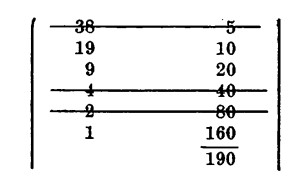
Lasciamo quindi al lettore il piacere di sbizzarrirsi in moltiplicazioni celeri. Prima però di passare a parlare della divisione vorremmo ancora accennare, riguardo alla moltiplicazione, a due utili metodi per un calcolo veloce da eseguirsi per iscritto anziché mentalmente. Se c’è da moltiplicare, poniamo, 38 • 5 potremo trovare in modo molto rapido il risultato se scriveremo i fattori, cioè i numeri 38 e 5 su due colonne; sotto al primo fattore scriveremo la metà di esso, poi, sempre in colonna, la metà della metà e così via sino a quando avremo trovato l’unità; se il numero fosse dispari, arrotonderemo per difetto; nell’altra colonna procederemo al contrario, scrivendo cioè il doppio del secondo fattore sotto quest’ultimo, quindi il doppio del doppio.
In conclusione
e e cancelleremo i numeri pari sulla prima riga e sommando poi i numeri rimasti sulla seconda colonna; il risultato trovato non sarà altro che il prodotto dei due numeri dati. La somma dei numeri restanti nella seconda colonna darà il prodotto voluto.
Infatti
Come si vede, la cancellazione viene eseguita con un sol tratto in modo da cassare anche i numeri della seconda colonna che si trovano in diretta corrispondenza dei numeri pari della prima.
Se abbiamo poi una moltiplicazione tra un numero di due cifre e il numero 11, potremo basarci sui seguenti due metodi:
a) se la somma delle due cifre è minore di 10 il risultato sarà un numero di tre cifre la cui cifra delle centinaia risulterà uguale a quella delle decine del moltiplicando. La cifra delle decine sarà invece uguale alla somma delle due cifre, mentre la cifra delle unità sarà uguale alla cifra delle unità, sempre del moltiplicando.
Es.: 45 • 11 = 495 .
– La cifra delle centinaia (4) è uguale a quella delle decine del numero (45).
– La cifra delle decine (9) risulta uguale alla somma delle due cifre del moltiplicando (4 + 5 = 9).
– La cifra delle unità (5) è uguale alla cifra delle unità del numero (45).
Apparentemente complicato tale metodo, come il precedente.