In questa guida spieghiamo quali sono le proprietà delle divisioni e vediamo come eseguire il calcolo.
Scritta la moltiplicazione 5 • 4 = 20 possiamo trasformarla in una uguaglianza (4 = 20 : 5) che chiameremo divisione, 20 : 5 = 4. Potremo perciò affermare che la divisione non è altro che l’operazione inversa della moltiplicazione e che il quoziente di due numeri (di cui il primo sia multiplo del secondo) è quel numero che, moltiplicato per il ‘secondo, dà come prodotto il primo; questo concetto possiamo esprimerlo anche sotto altra forma, chiamando quoziente di due numeri interi il più grande numero che moltiplicato per il secondo di tali numeri dà per prodotto un numero che non supera il primo.
Tale quoziente non varia se, posto che siano divisibili, si dividono o si moltiplicano i due numeri per uno stesso numero (proprietà invariantiva).
Anche per la divisione vi è la possibilità d’eseguire rapidi calcoli mentali.
A titolo d’esempio facciamo i seguenti calcoli elementari:
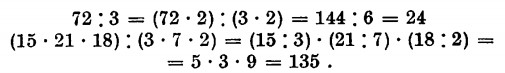
Abbiamo visto come la divisione sia un’operazione aritmetica tra due numeri, il dividendo e il divisore, che ci permette di ricavare un determinato valore chiamato quoto o quoziente che moltiplicato per il divisore ci dà il dividendo. Supposto di volere dividere il numero 25 per 5, avremo logicamente come quoto 5 e scriveremo l’operazione nella maniera già vista:
25 : 5 = 5 .
La stessa operazione la possiamo scrivere sotto un’altra forma con un segno aritmetico diverso senza che ne muti il valore. Un tale segno si chiama frazione. Questo significa che la semplice divisione si può scrivere come una frazione in cui il numero A (nel nostro caso 25) è diviso per il numero B (5). Abbiamo così tale forma
di scrittura:
in cui 25 è il numeratore (quello che nella divisione veniva chiamato dividendo), 5 è il denominatore (quello che nella divisione veniva chiamato divisore).
La linea di divisione si chiama linea di frazione. Sui banchi di scuola avrete certo udito l’esempio della torta che viene divisa in 4 parti o meglio 4 fette uguali tra loro; prendendo una fetta di questa torta avremo in mano 1/4 del dolce. La divisione sotto forma frazionaria significa cioè che prendiamo una o più parti di un determinato valore. In pratica: trovare 3/16 di 25,4;
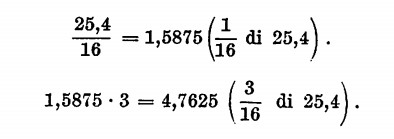
Tale numero è equivalente ai 3/16 di 25,4.
In sostanza abbiamo diviso per 16 il numero 25,4 e abbiamo preso il quoto tre volte.
Vogliamo ottenere ora gli 8/16 di 100 cioè dividere 100, per il numero 16 poi moltiplicarlo per 8 in modo da ricavarne otto parti (valore y); possiamo partire dalla considerazione che tanto 8 quanto 16 sono divisibili per 2, 4, 8 senza dare resto.
Per avere il valore y divideremo 8 per il numero più elevato che non dia resto (a patto che tale numero sia anche divisore di 16), poi divideremo ancora per lo stesso numero il numero 16. Otterremo così una frazione che ci permetterà di avere y; tale procedimento si chiama riduzione ai minimi termini.
Esempio
Uno dei segreti di tutte le operazioni con le frazioni sta quindi nel fatto che il numeratore e il denominatore possono esser moltiplicati o divisi da uno stesso numero senza che la frazione cambi di valore.
Passiamo ora al concetto di numero primo. Nella divisione abbiamo impiegato dividendi divisibili per 2, 3, 11, ecc. Vi sono però dei numeri, maggiori dell’unità, che non hanno altri divisori all’infuori dell’unità o del numero stesso. Questi sono i numeri primi. Gli altri numeri (quelli che cioè hanno divisori oltre l’unità o lo stesso numero) si dicono invece composti.
La serie dei numeri primi è illimitata. La loro importanza è enorme. Ogni numero intero che non sia primo può esser scritto come un prodotto di più numeri primi. In sostanza il più piccolo dei divisori di un numero (unità esclusa) sarà un numero primo.
