La velocità di una locomotiva la quale si sposti a marcia avanti può essere espressa per mezzo di un numero positivo ovvero da un numero preceduto dal segno +; la stessa locomotiva, quando si sposta a marcia indietro ha una velocità che noi esprimiamo con un numero negativo ovvero da un numero preceduto dal segno -.
Risulta essere in algebra che si usano numeri preceduti da un segno + o —; per fare ancora esempi di tali numeri, chiamati relativi, diremo che l’altitudine di una montagna sarà espressa da un numero positivo, mentre la profondità di un lago verrà espressa da un numero negativo; e ancora: osservando la scala termometrica centigrada, constatiamo che la sua gradazione va da 0° a 100° considerata come 0° la temperatura del ghiaccio fondente, come 100° quella dell’acqua in ebollizione. Dicendo: « Qui ci saranno almeno 20°» esprimiamo 20°, mentre dicendo : « In montagna il termometro scese a 150 sotto zero » intendiamo dire -150°. Quei numeri contrassegnati dal + o dal — sono riferiti a un numero che è lo 0. Per tornare all’esempio già citato dell’altitudine e della profondità, assumiamo come 0 il livello del mare, per cui, Bardonecchia sarà a + 1312 (1312 m d’altitudine), mentre il palombaro che scenda a 20 m di profondità, sarà a — 20 (20 m sotto il livello del mare).
Si mettano 9 palline in un recipiente contenente già 12 palline; indi se ne tolgano 15. Stabilito che il segno + stia a indicare la presenza di palline, mentre il segno — ne indichi l’assenza, il numero complessivo delle palline rimanenti, sarà dato da quella che si chiama somma algebrica, operazione che consiste nel riportare tutti i numeri con il loro segno ed eseguire le operazioni dai segni stessi
indicate:
+12+9-15 = + 6
numero indicante la presenza finale di 6 palline.
Dovendo conoscere quanti anni siano trascorsi tra la morte del grande geografo alessandrino Strabone, avvenuta nel 30 d. C., e la nascita del famoso medico Galeno (130 d. C.), è sufficiente eseguire la differenza 130 — 30 = 100. Conoscendo però la data di nascita di Strabone (63 a. C.) e volendo invece sapere quanti anni egli è vissuto, non sarebbe più possibile eseguire la differenza 30 — 63 ma è necessario fare la somma.
In realtà bisognerebbe dire che in entrambi i casi si esegue la differenza, ma è necessario aver presente che qualsiasi data, riferentesi ad avvenimenti accaduti prima dell’anno 0, viene espressa. da un numero negativo. Scriviamo pertanto:
(+ 30) — (— 63) = 30 + 63 .
Tale concetto ora visto di negativo o positivo, possiamo estenderlo a tutti i numeri dell’aritmetica siano essi interi o decimali o frazionari; sono ad esempio positivi
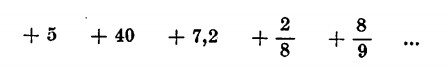
sono negativi:
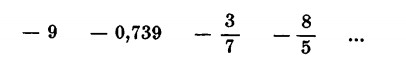
Immaginiamo ora dei numeri interi relativi disposti nel seguente ordine:
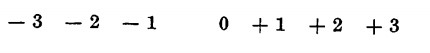
e disposti su una retta a distanza uguale l’uno dall’altro; attribuiamo alla retta un verso da sinistra verso destra lungo il quale questi numeri crescano di valore.
Il segmento sul quale ci si sposta da sinistra a destra per passare da un numero a quello immediatamente successivo, viene chiamato segmento unitario.
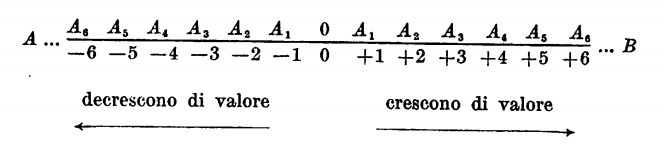
Per rappresentare un numero frazionario, quale ad esempio 7/4,
è sufficiente spezzare in quattro parti uguali il segmento unitario e riportare una di esse sette volte partendo dallo zero verso destra. Possiamo immaginare così di segnare su di una retta tutti i numeri frazionari.
In algebra è sempre possibile effettuare una sottrazione, cioè anche nel caso che il sottraendo superi il minuendo. Come abbiamo visto nell’esempio precedente una somma algebrica comprende sia l’addizione che la sottrazione e i numeri opposti che eventualmente si incontrano si annullano reciprocamente (esempio -2/3 + 2/3 = 0). Scrivendo un numero il quale non sia preceduto da alcun segno lo intendiamo come positivo, per cui scrivendo 5/6 , è come se avessimo + 5/6.
Per eseguire una somma di numeri decimali o frazionari, è sufficiente tener presente il segno, eliminando, s’intende ove è possibile, i numeri opposti. Esempio:
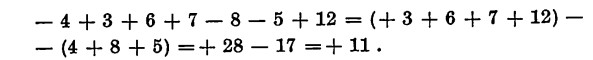
Analogamente
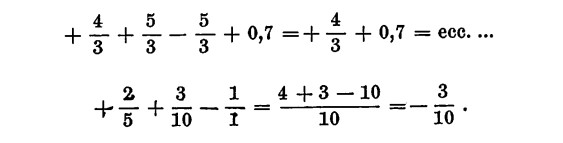
Se nel corso dell’esercizio incontriamo una parentesi preceduta dal segno positivo, non si farà altro che togliere la parentesi stessa senza cambiare il segno ai membri contenuti nella stessa parentesi. Se invece la parentesi in oggetto risulta preceduta dal segno —, tutti i termini in essa contenuti (attenzione a non dimenticarne qualcuno) vanno cambiati di segno quando togliamo la parentesi stessa. Vi sono vari tipi di parentesi; nell’ordine: graffa, quadra e tonda.
Esse vengono tolte iniziando a svolgere le operazioni tra parentesi tonda e procedendo via via con le quadro e con le graffe, e sempre facendo la massima attenzione ai segni.
Esempi
caso con segno positivo davanti alla parentesi
4 + (2 — 7 + 9 — 5) = 4 + 2 — 7 + 9 — 5 = + 3
caso con segno negativo davanti alle parentesi:
5 — (2 — 3 + 7 — 9) = 5 — 2 + 3 — 7 + 9 = + 8
caso con segni davanti a più parentesi:
— 7 — {— 5 — 3 — [— 2 + 6] + 4} — (— 5 + 7) =
=— 7 — {— 5 — 3 — [+ 4] + 4} — (+ 2) =
= — 7 + 5 + 3 + 4 — 4 — 2 =— 1 .
Avremo gli stessi segni dell’aritmetica anche per ciò che riguarda la moltiplicazione e la, divisione. Anche qui il segno della moltiplicazione viene espresso per comodità da un puntino, mentre il segno di divisione ( : ) viene sostituito dal segno di frazione. Ecco un pratico schema per i segni
Molto semplice da seguire.
