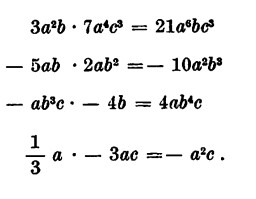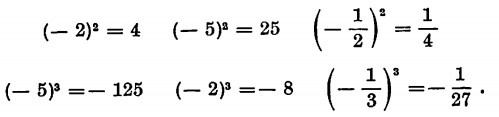In questa guida spieghiamo come eseguire le operazioni con i monomi.
Il monomio algebrico non è altro che il prodotto di due o più fattori numerici e letterali ed è intero se non ha nessuna lettera al divisore; in caso contrario sarà frazionario. Sia ad esempio un rettangolo; sappiamo che la base si indica con la lettera b, l’altezza con h e l’area con A.
Il monomio intero sarà A =b•h; il monomio frazionario sarà h = 
o anche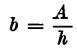 
. Nella geometria solida l’esempio può essere dato dal volume del cono (volume = V, raggio = r, π = 3,14, altezza = h): 
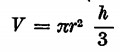(monomio intero) ; 
.
Il grado di un monomio rispetto a una lettera (ogni lettera figurerà infatti una volta sola) è quello della lettera stessa. Consideriamo i seguenti esempi
volume del cono: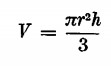 
(monomio di secondo grado)
volume della sfera: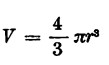 
(monomio di terzo grado), ecc…
Due o più monomi si dicono simili se hanno la stessa parte letterale:
sono simili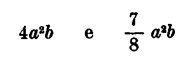 
Due monomi si dicono uguali quando oltre ad avere la stessa parte letterale hanno gli stessi coefficienti numerici:
sono uguali 
Eseguiamo qualche operazione con i monomi.
Indice
Addizione Monomi
Addizione: basta scriverli uno di seguito all’altro:
La somma di più monomi simili è un monomio simile ai dati, il cui coefficiente è la somma dei coefficienti degli addendi, esempio:
Valgono logicamente tutte le regole dell’aritmetica.
Sottrazione Monomi
Sottrazione: basta aggiungere al primo l’opposto del secondo:
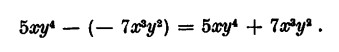
Per i monomi simili valgono le regole già esposte.
Moltiplicazione Monomi
Moltiplicazione: il prodotto di due o più monomi è un monomio che ha per coefficiente numerico il prodotto di tutti i coefficienti e per parte letterale il prodotto di tutte le lettere scritte una volta sola, e ciascuna lettera avrà per esponente la somma degli esponenti.
Esempi
Per la moltiplicazione valgono le seguenti proprietà:
a) un prodotto è nullo se è zero almeno uno dei fattori;
b) un prodotto è diverso da zero se nessun fattore è zero;
e) se due numeri uguali si moltiplicano per uno stesso numero si hanno prodotti uguali. Viceversa, se due prodotti di due fattori sono uguali ed hanno un fattore non nullo, gli altri due fattori sono uguali;
d) il prodotto di più fattori non nulli è positivo o negativo secondo che i fattori negativi sono in numero pari o dispari. In ogni caso il valore assoluto del prodotto è uguale al prodotto dei valori assoluti dei suoi fattori.
Divisione Monomi
La divisione invece è possibile se il monomio dividendo contiene tutte le lettere del monomio divisore con esponente maggiore o uguale al dividendo.
La divisione si può eseguire tra monomi interi e frazionari:
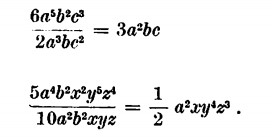
In sintesi occorre ricordare
a) dividendo lo zero per un numero relativo il quoziente rimane zero;
b) se dividiamo un numero relativo per zero l’operazione non ha significato;
c) dividendo un numero relativo per il suo contrario (opposto) il risultato rimane uguale a — 1 ;
d) il quoto cambia di segno quando dividiamo un numero relativo per — 1;
e) dividendo un numero relativo per + I il quoto rimane invariato;
f) dividendo un numero relativo per sé stesso il quoto è 1.
Potenza Monomi
La potenza di un monomio si ottiene elevando a potenza il coefficiente di ciascuna lettera (ricordare che la potenza di una potenza è uguale a una potenza che ha per base la. stessa base e per esponente il prodotto degli esponenti).
N.B.: qualunque numero elevato a esponente zero dà come risultato 1.
Per ciò che concerne i segni valgono le medesime regole dell’aritmetica; se la potenza è d’ordine pari il numero è sempre positivo, se dispari rimane il segno del numero
