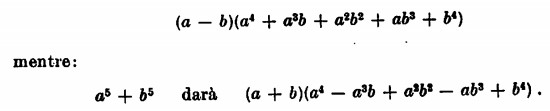I prodotti notevoli non sono altro che prodotti di polinomi i quali compaiono frequentissimamente nelle operazioni.
Il prodotto della somma di due monomi per la loro differenza è uguale alla differenza dei loro quadrati, il che può essere anche espresso dicendo che la differenza di due quadrati è uguale al prodotto della somma delle basi per la loro differenza. Il quadrato di un binomio è invece uguale al quadrato del primo termine più o meno il doppio prodotto del primo per il secondo più il quadrato del secondo. Analogamente il cubo di un binomio è uguale al cubo del primo termine più o meno il triplo prodotto del quadrato del primo termine per il secondo, più il triplo prodotto del primo termine per il quadrato del secondo più o meno il cubo del secondo termine.
La differenza di due cubi è invece uguale al prodotto della differenza delle basi per il polinomio formato dal quadrato della prima base più il prodotto delle due basi più il quadrato della seconda base.
La somma di due cubi è uguale al prodotto della somma delle basi per il polinomio formato dal quadrato della prima base meno il prodotto delle due basi più il quadrato della seconda base.
Vediamo a titolo di esempio la verifica algebrica del cubo di un binomio.
Sia dato invece
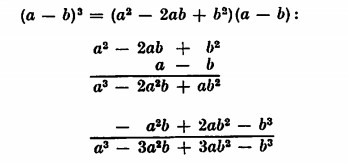
Sia ora il quadrato del binomio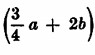 
; si avrà:
Il quadrato della differenza (a — b) dà a2 — 2ab + b2. Questo risultato ci è utilissimo per calcolare il quadrato di alcuni numeri.
Sia, per esempio, da calcolare il quadrato di 299; possiamo scrivere tale numero sotto la forma 300 — 1, per cui 2992 = (300 — 1)2.
Dalla (a2 — 2ab + b2) si ha che (300 — 1)2 = 90.000 — 600 + 1 = = 89.401.
Con un po’ di pratica si può pervenire a compiere tali quadrati mentalmente.
Tra gli altri prodotti notevoli abbiamo visto la differenza di due quadrati: a2 — b2 = (a + b)(a — b); tale risultato può esserci altrettanto utile. Si debba infatti calcolare 2012 — 1992; dalla (a + b)(a — n) si ha (201 + 199)(201 — 199) = (400 • 2) = 800.
Abbiamo già detto che la somma di due cubi si esprime come a3 + b3 = (a + b)(a2 — ab +b2); proviamo a verificare tale risultato:
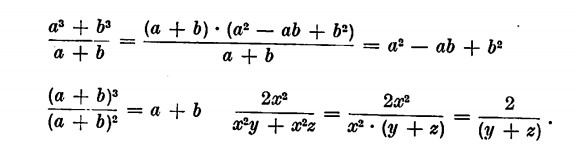
a5 – b5 darà invece
