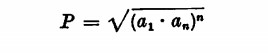In questa guida spieghiamo come si risolvono le successioni numeriche.
Se ad esempio scriviamo:
a1a2a3a4 .. an
avremo una successione, cioè un insieme di elementi che hanno ciascuno un posto determinato.
L’indice indica il posto che nella successione occupa ognuno di questi elementi.
Se in questa successione la differenza tra un termine e quello che lo precede è costante, avremo una progressione per differenza, ovvero una progressione aritmetica.
Avremo progressioni crescenti o decrescenti: la ragione di una progressione crescente è un numero positivo, quella di una progressione decrescente è un numero negativo.
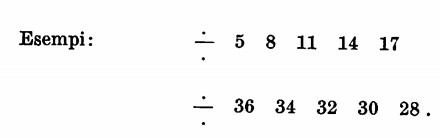
Nel primo caso la ragione è ovviamente + 3, nel secondo — 2. Il segno che abbiamo premesso alle due successioni scelte come esempi è quello che indica appunto la progressione.
Se ben osserviamo una progressione aritmetica, vediamo che ogni termine di essa è uguale al primo termine più il prodotto del numero dei termini precedenti a quello scelto per la ragione.
Questo discorso, apparentemente complicato, tratta della prima delle proprietà delle progressioni.
Vediamolo con un esempio; nella progressione già vista

la ragione (r) =+ 3.
Prendiamo il numero 17. Esso è uguale a 5 + (3 x 4) (infatti 5 + 12 = 17).
Se, data una progressione sommiamo gli estremi, constateremo che il risultato è uguale alla somma di due qualsiasi termini purché equidistanti dagli estremi.
Sempre basandoci sulla progressione già vista in precedenza
si avrà ad es.:
5 + 17 = 8 + 14 (22 = 22).
Avremo cosi dimostrato la seconda delle proprietà.
Se sommiamo n termini consecutivi di una progressione aritmetica, constateremo che tale somma corrisponde a n volte la media aritmetica dei termini estremi. Infatti:
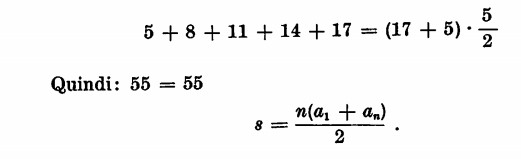
Vediamo ora le stesse proprietà esaminate nella applicazione pratica.
Se dovessimo esaminare gli angoli di un pentagono convesso (la cui somma è 540 gradi) sapendo che essi sono in progressione aritmetica di ragione 10 gradi, avremo una progressione aritmetica di 5 termini (5 angoli del pentagono), per cui considerata la progressione

che sarà uguale a 540; da cui x = 108 e gli angoli risulteranno 88, 98, 108, 118, 128 gradi.
Vediamo ora in particolare quella proprietà esaminata precedentemente, per cui ogni termine della progressione era uguale al primo termine + il prodotto dei termini precedenti quello scelto per la ragione.
Se infatti si ha la progressione
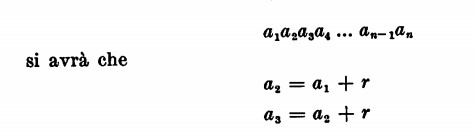
Se sommiamo tra di loro i primi membri e i secondi e sopprimiamo i termini comuni si avrà che:
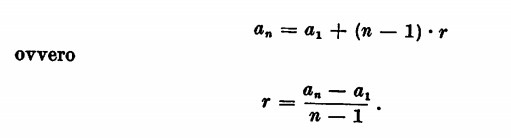
Potremo così inserire dei medi aritmetici, cioè: se dati due numeri a e b si deve determinare n numeri tali che formino, con a e b come estremi, una progressione aritmetica, con la formula testé vista, la ragione di questa progressione che noi dobbiamo trovare sarà uguale a:
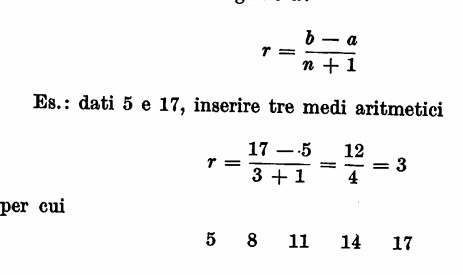
Progressione per quoto o progressione geometrica.
Risulta essere una progressione in cui il quoto tra un numero e il suo precedente è costante. Questo quoto è la ragione della progressione geometrica.

Sarà una progressione geometrica anche una successione di potenze di 10 con esponente 1, 2, 3, ecc. (10, 100, 1000).
Ogni progressione geometrica viene preceduta dal segno ![]() .
.
Un termine qualunque di una progressione geometrica è uguale al prodotto del primo termine per la ragione elevata a esponente uguale al numero dei termini che precedono questo termine stesso.
Infatti nella progressione precedentemente esaminata si aveva che:
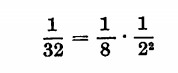
Ciascun termine viene a essere il medio geometrico tra quello che lo precede e quello che lo segue (da cui il nome di progressione geometrica).
Vediamo come si può effettuare la somma (S) dei termini di una progressione geometrica.
S = a1 + a2 + a3, ecc. Poiché questa somma di termini consecutivi è
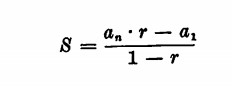
mentre il prodotto di n termini consecutivi è pari alla radice quadrata del prodotto degli estremi all’n potenza: