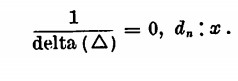In questa guida spieghiamo cosa sono i logaritmi e quali sono le loro proprietà.
Data la potenza an e considerato n razionale, si ha:
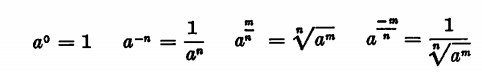
se invece n è un numero irrazionale, ovvero è un elemento di separazione di due classi convergenti, la potenza ax non è altro che un elemento di separazione di due classi, a4, a4′; in genere si è sempre avuto il medesimo problema: data la base e l’esponente trovare la potenza.
L’operazione dell’elevazione a potenza dà, però luogo a due operazioni inverse, come: data la potenza e l’esponente trovare la base, oppure data la potenza e la base trovare l’esponente. Questo esponente da trovare, o meglio da assegnare a una determinata base per ottenere una determinata potenza, si chiama logaritmo; la scrittura loga b = x si legge logaritmo di b in base a. In conclusione si chiama logaritmo di un numero b rispetto alla base a l’esponente reale x al quale bisogna elevare la base per avere il numero dato b. Facciamo qualche esempio:
(nel primo caso 102 = 100, nel secondo 53 = 125).
Il logaritmo di un numero b rispetto ad a (base reale positiva diversa da 1) esiste sempre ed è, si intende, unico. Allorché ricerchiamo il logaritmo di un numero rispetto a una base data, compiamo una ricerca o estrazione di logaritmo. Consideriamo due progressioni crescenti e indefinite, la prima per quoziente e l’altra per differenza; i termini della progressione per differenza si chiamano i logaritmi dei termini corrispondenti nella progressione per quoziente.
Se si inserisce una serie di medi tra i termini consecutivi delle due progressioni, ne consegue che i termini introdotti nella progressione per differenza, saranno ancora i logaritmi dei termini introdotti nella progressione per quoziente.
Si ha cioè un sistema di logaritmi e in conclusione il logaritmo di un numero dipende dalla sua scelta. Esempio:
Qualunque sia la base il logaritmo dell’unità corrisponde a zero; il logaritmo di una potenza della base è uguale all’esponente e il. logaritmo della base è uguale all’unità.
Da notare che:
il logaritmo di un prodotto è uguale alla somma dei logaritmi dei singoli fattori, mentre il logaritmo di un quoziente è uguale alla differenza tra il logaritmo del dividendo e quello del divisore; il logaritmo di una potenza è uguale al prodotto dell’esponente per il logaritmo della base della potenza, mentre il logaritmo di un radicale è uguale al logaritmo del radicando diviso l’indice del radicale.
Da tutto ciò si deduce che, passando dai numeri ai logaritmi, il prodotto si muta in somma, il quoziente in differenza, l’elevazione a potenza in moltiplicazione per l’esponente, l’estrazione della radice in divisione per l’esponente. In qualsiasi sistema i logaritmi di due numeri reciproci sono uguali ma di segno contrario; il logaritmo di 
si dice cologaritmo, il quale è uguale al logaritmo del numero col segno cambiato.
Nota: le potenze di 10 con indice intero hanno per logaritmo il loro esponente. I logaritmi dei numeri che non sono potenze di 10, sono numeri decimali, illimitati, non periodici (irrazionali).
La parte intera di tale numero si chiama caratteristica, mentre la parte decimale si chiama mantissa. Numeri di due cifre avranno per caratteristica 1, mentre numeri di una sola cifra avranno per caratteristica 0. Nel sistema decimale, la caratteristica di un numero maggiore di 1 è positiva (= al numero delle cifre della parte intera del numero dato diminuito di un’unità). Esempi:
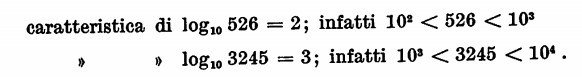
In sostanza nel sistema decimale la caratteristica di un numero positivo minore di 1 è negativa. Abbiamo parlato della caratteristica; vediamo ora di considerare la mantissa. Moltiplicando o dividendo un numero per una potenza intera di 10 la caratteristica aumenta o diminuisce di tante unità quante sono quelle dell’esponente della potenza di 10; la mantissa invece non si altera.
Abbiamo detto che il logaritmo di un numero, indicato simbolicamente con log, è composto di una parte intera detta caratteristica e di una parte decimale detta mantissa.
La caratteristica del logaritmo in base 10 di un numero > 1 è data da tante unità positive quante sono le cifre intere di quel numero meno un’unità. Quella del logaritmo di un numero < 1 è data da tante unità negative quanti sono gli zeri che precedono la prima cifra significativa, compreso lo zero prima della virgola. Il segno — si scrive sulla caratteristica:
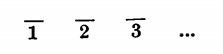
Facciamo qualche esempio:
la caratteristica di 6439 è 3 (infatti il numero è composto di quattro cifre: 4 — 1 = 3).
Così la caratteristica di 137.964 è 5 (6 — 1 = 5)
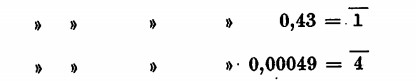
La mantissa si ricerca invece sulle tavole compilate appositamente dagli studiosi; praticamente per trovare il logaritmo di un numero bisogna osservare che:
— se il numero è compreso tra 1 e 10.000 ci si servirà della tavola I;
— se il numero è superiore a 10.000 si dovrà fare l’interpolazione.
In quest’ultimo caso il procedimento è il seguente:
si debba per esempio calcolare il logaritmo di 379495, la cui caratteristica è 5; la mantissa si trova nel seguente modo:
si cerchi sulla tavola I la mantissa di 3794 (si considera il numero formato dalle prime tre cifre) che è 57.910 e la mantissa di 3795 che è 57.921.
Questi due numeri ci servono poiché teoricamente si suppone che gli incrementi dei logaritmi siano proporzionali agli incrementi dei numeri; partendo da questo presupposto l’errore che si commette nel calcolo è di scarso rilievo. Si calcola ora la differenza tra le due mantisse che è 11. A questo punto si consulta la tabella delle parti proporzionali (P.P.) prendendo in considerazione proprio il numero 11.
Per esso si moltiplicano separatamente le cifre rimanenti del numero di cui vogliamo trovare il logaritmo (9 e 5) tenendo presente che esse assumono un valore decimale progressivo come se si trovassero dopo la virgola. Quindi 0,9 e 0,05.
Eseguiamo le operazioni:
0,9 • 11 — 9,9
0,05 • 11 = 0,55 .
Riprendiamo ora la mantissa di 3794 che è 57.910 e ad essa sommiamo i valori trovati. Avremo allora:
Il logaritmo avrà per mantissa 57.920 (escludendo le cifre decimali). Il logaritmo di 379.495 è pertanto 5,57920.
Nel caso che il numero sia superiore a quelli registrati sulle tavole ci serviremo delle prime cifre del numero dato e cercheremo la mantissa corrispondente a questo nuovo numero previa una piccola correzione; per meglio chiarire ciò bisognerebbe enunciare il teorema per cui dati numeri abbastanza grandi le loro differenze sono proporzionali — sia pure con notevole approssimazione — alle differenze dei logaritmi.
La differenza che si ha tra due logaritmi successivi ha nome di differenza tabulare e si indica con delta maiuscolo 
. Questa differenza è segnata sulle tavole stesse (qualora si aumenti il numero di 1) mentre se si aumenta il numero di una parte decimale
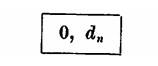
si avrà un aumento del logaritmo di una quantità x data dalla seguente proporzione
