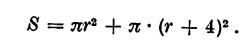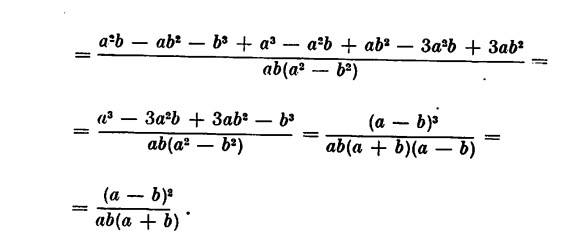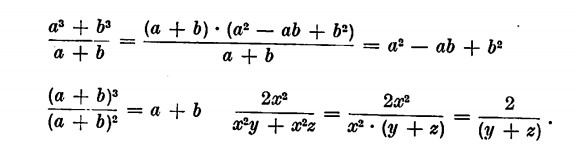Per polinomio intendiamo la somma algebrica di più monomi.
Dalla geometria possiamo ricavare esempi molto semplici; sommando cioè l’area di un cerchio di raggio r con quella di un cerchio di raggio r + 4 si ha un binomio
Il grado assoluto di un polinomio è dato dal massimo grado di uno dei suoi monomi
è un polinomio: il suo primo termine è di quarto grado ma è anche il termine che ha il grado più alto quindi il polinomio stesso è di quarto grado.
Un polinomio si dice omogeneo allorché i termini hanno tutti il medesimo grado.
Un polinomio può esser ordinato secondo una lettera quando quasi tutti i termini la contengono; allora si potrà disporre gli stessi termini secondo le potenze crescenti o decrescenti di quella lettera. Considerando, il polinomio già visto e volendo ordinarlo secondo la lettera y si avrà:
![]()
Se i termini di un polinomio sono due, si chiamerà binomio, se invece sono tre si chiamerà trinomio.
Le operazioni di una certa importanza sono il quadrato di un binomio, il prodotto somma per differenza di due monomi, il cubo, la scomposizione in fattori e così via. Esempi:
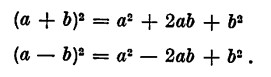
Per addizionare due o più polinomi basta scrivere i termini dell’uno di seguito a quelli dell’altro, ciascuno con il proprio segno. Per sottrarre da un polinomio un altro polinomio si scrivono di seguito ai termini del primo tutti i termini del secondo con il segno cambiato.
La riduzione dei termini simili si effettua sostituendo a tutti gli addendi simili tra loro un unico termine che ha la stessa parte letterale e come coefficiente la somma algebrica dei coefficienti. Dall’esempio precedente si ricava la seguente regola
il quadrato di un binomio è uguale al quadrato del primo termine il doppio prodotto del primo per il secondo, più il quadrato del secondo,
Prodotto somma per differenza di due monomi
![]()
La scomposizione in fattori rende poi possibile ciò che sembrerebbe impossibile.
Esempio
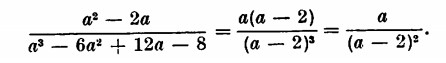
La scomposizione in fattori algebrici è identica a quella aritmetica.
Non c’è infatti alcuna differenza tra i due procedimenti:
Primo Esempio:
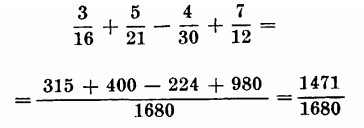
Scomposizione in fattori e m.c.m.:
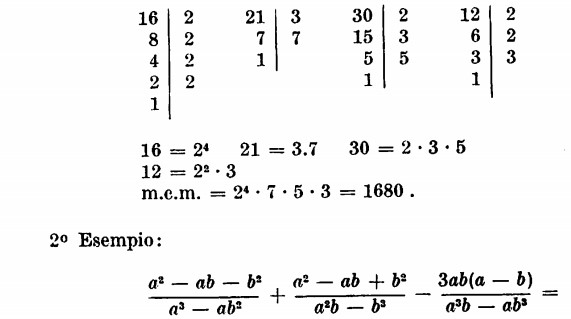
Scomposizione in fattori dei denominatori
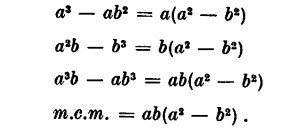
Vediamo ora un semplice esercizio sul cubo di un binomio
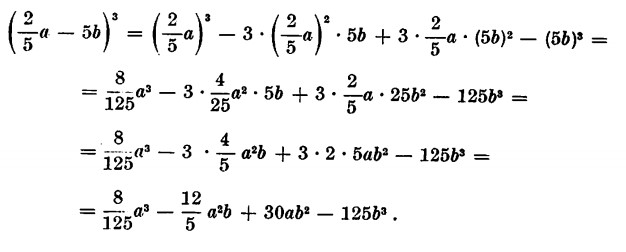
e uno sul prodotto della somma per la differenza di due monomi:
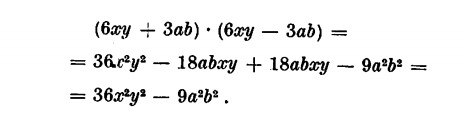
Il quadrato di un polinomio è uguale alla somma dei quadrati dei suoi termini aumentata di tutti i possibili doppi prodotti dei termini stessi presi a due a due.
Esempio
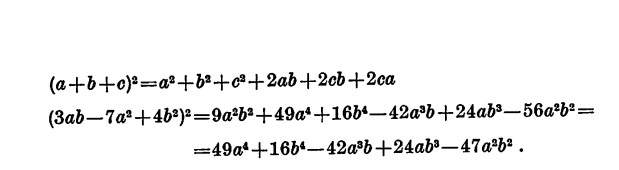
N.B.: i quadrati sono sempre positivi mentre il segno dei doppi prodotti dipende dal segno dei singoli monomi.
Cubo di un binomio: esso è uguale al cubo del primo termine, più il triplo prodotto del quadrato del primo per il secondo, più il triplo prodotto del primo per il quadrato del secondo, più il cubo del secondo.
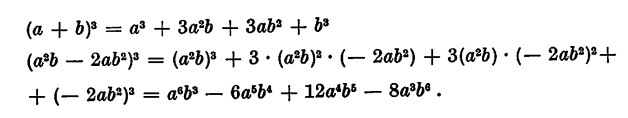
Cubo di un trinomio:
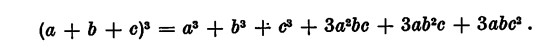
Se tutti i termini di un polinomio sono divisibili per uno stesso monomio il polinomio dividendo si può considerare come il prodotto di due fattori: l’uno è il divisore comune (fattore comune che si mette in evidenza) e l’altro è il quoziente tra il polinomio dato e il fattore messo in evidenza.
Perciò per mettere in evidenza un fattore comune in un polinomio, basta cercare il M.C.D. dei termini; lo si moltiplica poi per il polinomio ottenuto dividendo il polinomio dato per il fattore posto in evidenza:
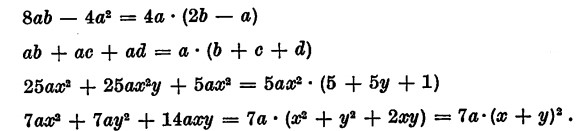
Raccoglimento a gruppi
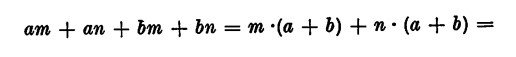
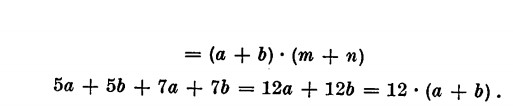
Differenza di due quadrati
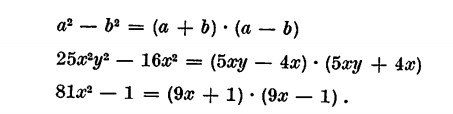
Tener presente i due casi particolari
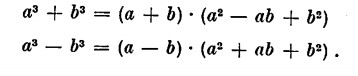
Qualche esempio di semplificazione