Basta che ci guardiamo attorno per constatare come qualsiasi oggetto sia tridimensionale e oltre a una superficie occupi anche un certo spazio misurato dal volume dell’oggetto stesso.
Indubbiamente la figura solida che abbiamo incontrato più spesso è il cubo. La superficie di tale solido sarà data dalla formula:
S = 6 x l3
infatti sviluppando il cubo si ottengono 6 quadrati uguali. Il volume è dato invece dalla formula; V = l3, in pratica si ottiene facendo il cubo della lunghezza dello spigolo; dalla formula che abbiamo
visto ora, si ricava il lato: ![]() .
.
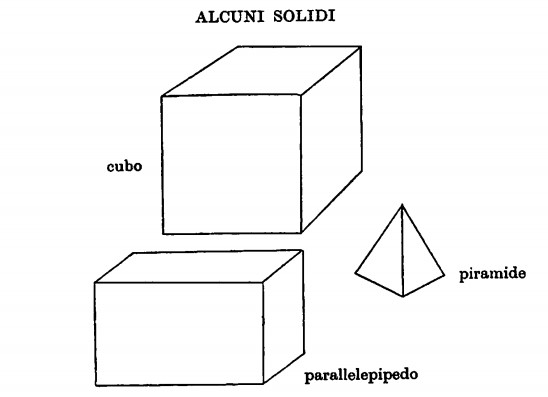
Un’altra figura comunissima è il parallelepipedo rettangolo; quasi tutte le scatole hanno tale forma per non parlare che degli oggetti di uso più comune; diremo che il parallelepip.edo rettangolo è un poliedro formato da 6 rettangoli a due a due paralleli.
Il suo volume sarà dato dal prodotto area per altezza o meglio dal prodotto della lunghezza della base per l’altezza per la profondità (V = a • b • c).
Solido « antichissimo » è poi la piramide, nome che ci riporta alla mente le costruzioni dell’antico Egitto.
Gli egiziani eccellevano nell’erigere tali costruzioni tombali dalle enormi dimensioni. La piramide di Cheope ad esempio, ha il lato di quasi 230 metri e l’altezza di 146, dimensioni che fanno letteralmente strabiliare. Generalmente una piramide era costruita con blocchi di calcare ed eretta con il concorso di migliaia di schiavi.
Costruite sulla sponda occidentale del Nilo queste tombe hanno sempre suscitato l’ammirazione di quanti, viaggiando dal Cairo a el-Faiyum (l’antica Setje), si sono trovati alla loro presenza. Lo stesso Napoleone il 21 luglio dell’anno 1798 ammoniva i suoi soldati con la celebre frase: «…40 secoli vi guardano ». Una circostanza che dimostra quanto i loro architetti fossero versati in astronomia è data dal fatto che la luce di Sirio, la stella distante da noi 9 anni luce, illumina a perpendicolo la faccia meridionale di tali costruzioni.
Immaginiamo ora di far ruotare un rettangolo sul proprio lato più lungo; la figura così idealmente ottenuta è un cilindro; cilindrici sono quasi tutti i recipienti che conosciamo (le lattine di birra, tanto per fare un esempio). Un cono lo si potrà ottenere idealmente facendo ruotare un triangolo attorno ad un lato, mentre la sfera sarà data dalla rotazione di un semicerchio attorno al diametro. La sfera è uno dei solidi più interessanti. I cuscinetti a sfera, ad esempio, sono indispensabili nelle costruzioni meccaniche riducendo al minimo gli attriti. Anche questa figura, come quella del cubo, ci è familiare sin dall’infanzia: la prima palla di gomma.
Una sfera non è sviluppabile su di un piano, il che provoca notevoli difficoltà, quando dobbiamo rappresentare parte della superficie terrestre.
La terra ha infatti — grosso modo — figura sferica; sferici sono anche i contenitori di gas, i palloni aerostatici, e senza sfera non vi sarebbero tifosi del gioco del calcio o accaniti giocatori di biliardo. Sin dalla antichità, la sfera fu oggetto di studio e sarà sufficiente citare Archimede che ne determinò per la prima volta il volume, per non parlare della dimostrazione di L. Valerio (dimostrazione della scodella, come è chiamata negli scritti di Galileo).
Altri solidi interessanti sono i poliedri regolari, cioè figure solide che hanno per facce dei poligoni regolari: alcuni li abbiamo già visti, ad esempio il cubo e la piramide; qui invece intendiamo parlare del tetraedro, dell’ottaedro e dell’icosaedro, cioè solidi le cui facce sono triangoli; il tetraedro è una specie di piramide a base triangolare, l’ottaedro è un solido che ricorda due piramidi combacianti per la base quadrata, l’icosaedro è un solido limitato da una superficie formata da venti triangoli; vostra moglie lo conoscerà senz’altro dato che molti diamanti sono tagliati secondo tale forma.
Rimane ancora da citare il dodecaedro regolare che è limitato da una superficie formata da 12 pentagoni. Anche questo solido è tutt’altro che sconosciuto alla vostra consorte; infatti molte pietre preziose, specie se di gran valore, ancorché piccole, vengono tagliate proprio con questa forma.
Abbiamo dato così un’occhiata en passant in casa della geometria solida.
Formule Solidi
Facciamo quindi seguire una piccola tabella esplicativa contenente alcune formule per la determinazione sia delle aree di figure piane che di volumi di solidi.
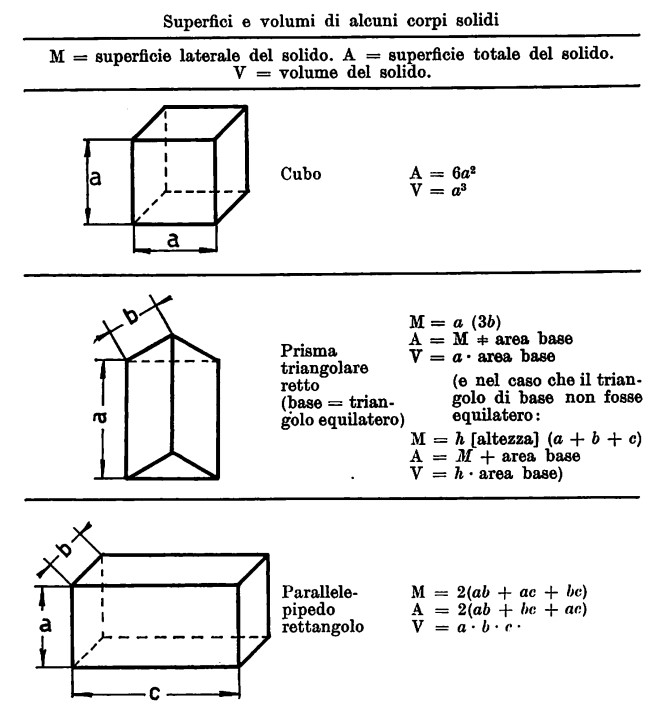
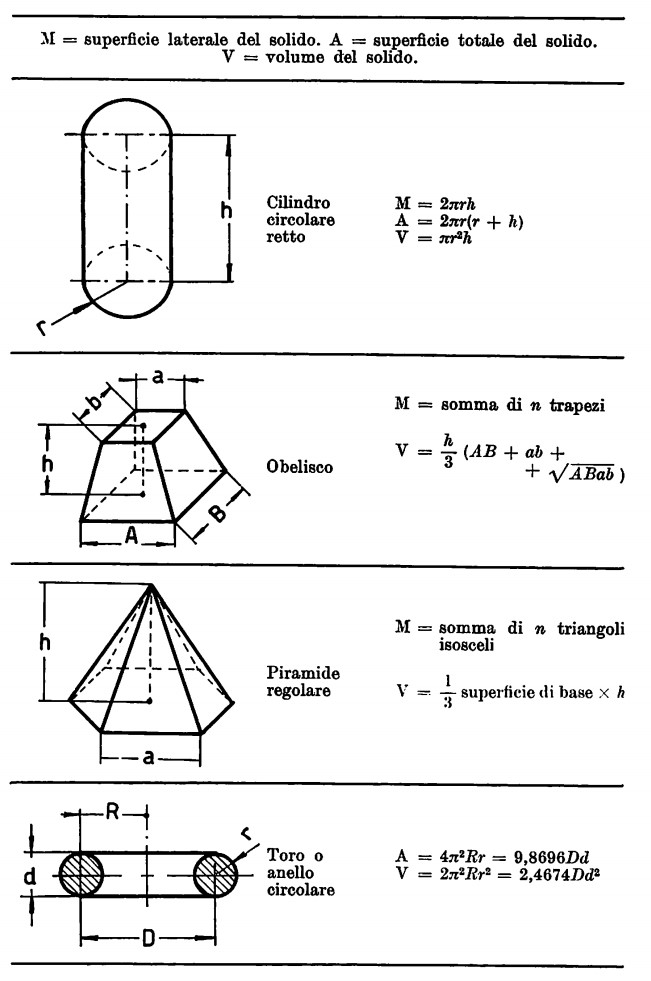
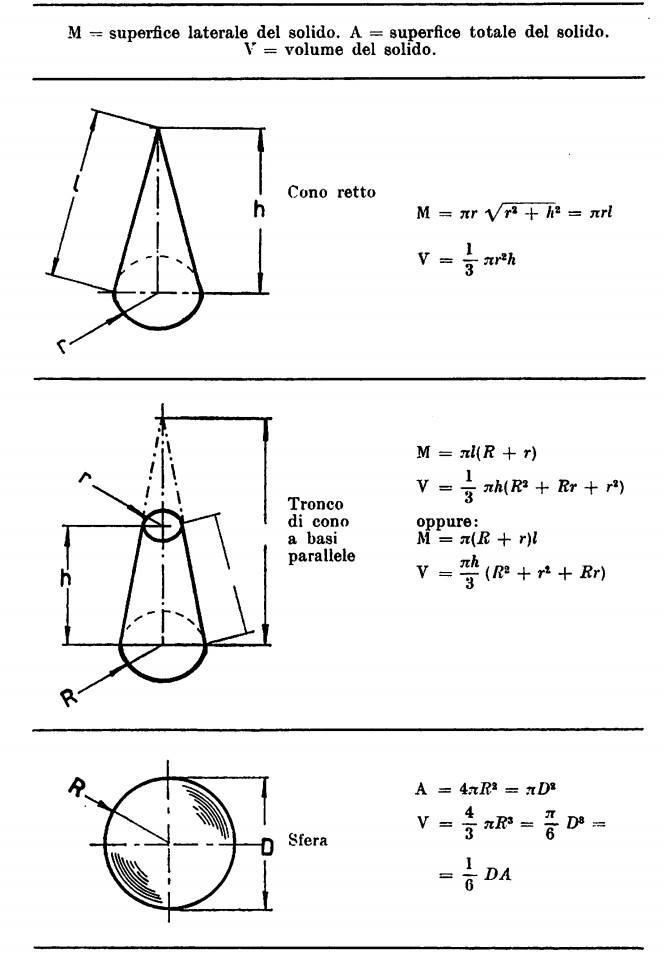
Problemi con i Solidi
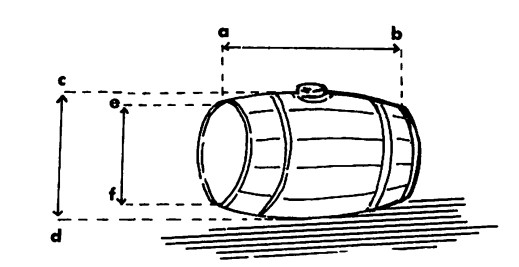
Volume di una botte
Una botte è generalmente a sezione circolare con due diametri, uno maggiore e uno minore; indicando con D il diametro maggiore e con d quello minore, volendo calcolarne, sia pure in maniera approssimativa, il volume potremo servirci della seguente formula:
V = 0,087 • L•(d+ 2D)2
L = lunghezza
0,087 = numero fisso.
Negli uffici del dazio viene anche usata la seguente formula
V = 0,82 •L•d• D
Questa formula è detta « formula di Guilmin ».
Lasceremo al lettore calcolare ora la capacità di una botte con la « formula di Guilmin », botte che ha le seguenti misure:
ab = 1,70 cd = m 1,10 cf = m 0,80
Un vero problema
Un muratore decide di calcolare la costruzione di un blocco di cemento a forma di cubo avente il lato di un metro e poggiante su quattro sottili colonne di sezione quadrata (lato del quadrato: 10 cm).
Avendo scoperto che il suo cubo pesa ben due tonnellate, il nostro bravo muratore constata come su ognuna delle colonne gravi un peso di 500 kg, per cui su ogni cm2 di essa si esercita una forza di 5 kg, considerato anche che la superficie d’appoggio della colonna è di 100 cm3. Se ognuna delle colonne è stata concepita per sopportare un peso maggiore (poniamo 8 kg per centimetro quadrato) la costruzione non crolla.
Il nostro muratore si domanda ora se sia, possibile aumentare le dimensioni della costruzione avvalendosi sempre del medesimo materiale. Prova allora a calcolare: raddoppiando il lato del cubo il volume dello stesso diviene di 8 m3 e il peso di 16.000 kg.
Ognuna delle colonne si trova a sorreggere 4000 kg, e ha ora una superficie d’appoggio di 400 cm2. Pur avendo raddoppiato il lato delle colonne la costruzione non regge, posto che su ogni centimetro quadrato si ha una pressione di 10 kg, poiché se l’area è quattro volte maggiore i volumi, e i pesi, sono otto volte maggiori e a tale pressione il materiale cede.