Un numero risulta divisibile per un altro quando, scomposti i due numeri in fattori, si constata che il primo dei due numeri contiene tutti i fattori primi del secondo, naturalmente con esponente maggiore o uguale.
Possiamo però dire che un numero è divisibile per 2 qualora termini con uno zero o con una cifra pari.
Un numero terminante con zero sarà sempre divisibile per il numero 10 (e così un numero terminante con due zeri sarà divisibile per 100, con tre zeri per 1000…).
Un numero risulterà divisibile per 4 quando avremo un multiplo di 4 formato dalle due ultime cifre a destra (esempio: 124).
Un numero sarà divisibile per 5 se termina per 5 o 0 (sarà divisibile per 25 se termina con due zeri oppure con 25, 50, 75, …).
Un numero è divisibile per 3 o per 9 quando la somma delle sue cifre è divisibile per 3 o per 9 (esempio: 135).
Un numero è divisibile per 11 se la somma delle cifre che occupano posti dispari meno la somma delle cifre che occupano posti pari, dà per risultato un numero divisibile per 11 (esempio: 2827).
Consideriamo ora più numeri (5, 10, 15, 20…) ; se uno di tali numeri è divisore di tutti gli altri, avrà nome di massimo comun divisore (M.C.D.). Il massimo comun divisore sarà sempre il più grande tra i divisori comuni.
Allorché noi dobbiamo trovare il M.C.D. tra due o più numeri dovremo scomporre i numeri stessi in fattori primi e moltiplicare tra loro i fattori comuni (presi ciascuno con il minimo esponente). In pratica però si possono anche seguire i seguenti metodi:
a) se i numeri sono due, divideremo il maggiore per il minore; se tale divisione dà per resto zero, il minore tra i due numeri sarà il massimo comun divisore. In caso si ottenga un resto diverso da zero, divideremo il più piccolo dei numeri per il resto e così via fino a ottenere per resto zero. L’ultimo divisore da noi adoperato, quello che cioè ci ha dato ancora un resto diverso da zero, sarà il M.C.D. richiesto.
b) Se i numeri sono tre o più, ci serviremo del metodo precedente per ottenere il M.C.D. tra due qualsiasi di tali numeri. Procederemo poi trovando il M.C.D. tra quello ottenuto in precedenza e un altro qualsiasi dei numeri, e così via fino ad avere esaurito tutta la serie dei numeri dati. Il M.C.D. degli ultimi due numeri sarà quello cercato.
In generale diremo ancora che, se due o più numeri vengono moltiplicati per uno stesso numero, anche il M.C.D. viene moltiplicato per tale numero. Se invece due o più numeri vengono divisi per uno stesso numero, anche il M.C.D. viene diviso per tale numero. Questi stessi numeri divisi per il loro M.C.D. daranno dei quoti primi tra di loro. In pratica vediamo con degli esempi come si applicano tali regole.
Il metodo a è chiamato anche il metodo delle divisioni successive o algoritmo di Euclide. La parola algoritmo significa metodo di calcolo.
Questo algoritmo di Euclide permette di risolvere problemi del tipo: « Dati due numeri A e B (positivi) trovare il M.C.D. t>, esisteranno tanti problemi di tale tipo quante sono le diverse coppie di A e B; ognuno di tali problemi si risolve, come abbiamo visto, costruendo una successione decrescente di numeri:
A (maggiore di B). B (minore di A),
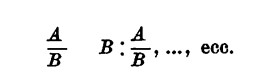
ovvero come è stato scritto « …divideremo il più piccolo dei numeri per il resto… ».
Sappiamo che l’esecuzione di un’operazione di divisione si può ridurre a una esecuzione di sottrazioni successive. Dovendo impartire necessarie istruzioni a un calcolatore elettronico, si potrà procedere come segue:
istruzione n. 1 prendere in considerazione A e B;
istruzione n. 2 confrontare tali numeri e vedere qual è il maggiore;
istruzione n. 3 se i due numeri sono uguali il calcolo si ferma (abbiamo detto che « …se tale divisione — cioè tra il maggiore e il minore — dà per resto zero, il minore tra i due numeri sarà il M.C.D. »; ciò presuppone : che vi sia un numero maggiore e uno minore; è inevitabile quindi che, se i due numeri risultano uguali ognuno dei due sarà il M.C.D.;
istruzione n. 4 se il primo numero risulta minore del secondo invertiremo i numeri;
istruzione n. 5 procedere alla sottrazione del secondo numero dal primo e sostituire i numeri dati col sottraendo e con la differenza (che chiamiamo qui per comodità a e b).
Ricomincia pertanto il ciclo e l’istruzione n. 6 sarà uguale alla istruzione n. 1 (prendere in considerazione a e b).
I casi da ricordare
a) Un numero è divisibile per 2 quando è pari.
b) Un numero è divisibile per 4 quando il numero formato dalle due ultime cifre, a destra, è divisibile per 4.
e) Un numero è divisibile per 5 quando termina con 0 o con 5.
d) Un numero è divisibile per 10 se termina con uno zero.
e) Un numero è divisibile per 100 se termina con due zeri.
f) Un numero è divisibile per 1000 se termina con tre zeri, ecc.
g) Un numero è divisibile per 25 quando il numero formato dalle due ultime cifre a destra è divisibile per 25.
h) Un numero è divisibile per 3 o per 9 quando la somma delle sue cifre è divisibile per 3 o per 9.
i) Un numero è divisibile per 8 quando il numero formato dalle tre ultime cifre a destra è divisibile per 8.
l) Un numero è divisibile per 125 quando il numero formato dalle tre ultime cifre a destra è divisibile per 125.
m) Un numero è divisibile per 11 quando la maggiore delle somme che si ottengono considerando alternativamente le cifre del numero, diminuita dalla minore, dà. un risultato divisibile per 11. Si può anche dire che risulta divisibile per 11 quel numero che, diviso in numeri di due cifre partendo da destra, presenta la somma di tali numeri divisibili per 11.