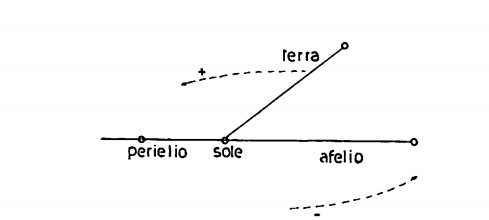
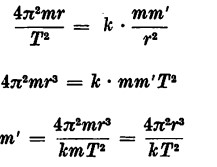Quando sui banchi del liceo studiavamo geografia, il parlare del sole era tutt’uno con il parlare di Copernico e soprattutto di Keplero. Vi ricordate la famosa legge che diceva: I pianeti descrivono intorno al sole delle orbite ellittiche di cui il sole occupa uno dei fuochi ?
Personalmente ricordo soprattutto il tono monotono della professoressa la quale inesorabilmente spiegava come da questa legge (la prima) discendessero alcune importanti deduzioni; il sole non si trova sempre alla medesima distanza dal pianeta e neppure al centro della stessa ellisse. Ma che cos’è questa ellisse
E qui veniva fuori il nome di Apollonio, quel grande geometra dell’antichità,: l’ellisse è una linea piana, linea geometrica rappresentata da due punti detti fuochi posti all’interno di essa e risulta dall’insieme di tutti i punti del piano tali che la somma delle loro distanze dai fuochi sia costante.
Ed ecco che eravamo costretti a tirar fuori il foglio da disegno e dopo averlo fissato sul banco prendevamo una riga; tracciavamo una retta e su questa sistemavamo due puntine da disegno; poi, preso un filo collegavamo una puntina all’altra; premendo la matita contro il filo eravamo così in grado di disegnare ellissi quasi perfette, dico quasi perché a me capitava sempre di disegnare un uovo perfetto.
Quella retta sulla quale avevamo piantato le puntine — rappresentanti i fuochi — era l’asse maggiore; a metà, strada tra i fuochi era il centro dell’ellisse da noi tracciata.
Preso poi a piacere un punto sull’ellisse stessa e unitolo con un segmentino a uno dei fuochi, ottenevamo il cosiddetto « raggio vettore », cioè la distanza del punto mobile dal fuoco, rappresentata naturalmente in lunghezza e direzione.
Mi ricordo soprattutto dei calcoli fattici inopinatamente fare dalla professoressa di scienze sulle sezioni ellittiche. C’era in particolare il problemino dei volumi dei caratelli. Il caratello, si sa, è una piccola botte a sezione ellittica e il suo volume lo si ottiene con la seguente formula:
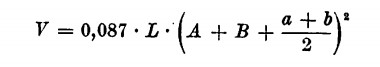
nella quale:
L = lunghezza
A, B = assi della sezione maggiore
a, b = assi della sezione minore.
Tornando alla terza legge di Keplero, sappiamo che un pianeta impiega un determinato periodo di tempo per percorrere la sua ellisse. Se vogliamo misurare la durata di tale periodo in anni terrestri, dovremo basarci necessariamente sulla distanza media dello stesso pianeta dal sole.
In base alla legge di Keplero ora vista, si ha che 
è una costante (per t intendiamo il periodo o tempo mentre con D si intende la distanza). Ora se t è uguale a un anno e D è un U. A. (unità astronomica) si ha che questa costante è pari a 1. Questo nel caso della terra.
Per la seconda legge di Keplero, abbiamo che la velocità V del pianeta è uniforme ed è proporzionale al raggio dell’orbita D mentre è inversamente proporzionale al tempo t impiegato a percorrerla. V è proporzionale 
per cui 
è ovviamente proporzionale a 
ma poiché per la terza legge 
è una costante, e ciò vale anche — ovviamente — per il suo inverso, si ha che: , e necessariamente , è proporzionale a 
, ciò che ci dimostra come il quadrato della velocità dei pianeti sia inversamente proporzionale alla distanza dal sole. I dati che alleghiamo chiariscono meglio ciò che intendiamo dire.
Immaginiamo ora un faro il quale, posto su uno scoglio, spazzi il cielo coprendo un’area. Supponiamo ora che il faro sia il sole e che il fascio luminoso sia il raggio vettore, segmento ideale che unisce il sole a un pianeta. Allorché il pianeta si trova in prossimità del sole, se noi consideriamo l’area da coprire pari ad A, compirà un certo percorso; sempre considerando pari ad A l’area, il percorso sarà minore allorché il pianeta sarà lontano dal sole.
In altre parole a mano a mano che il pianeta si avvicina al sole aumenta la propria velocità, mentre quest’ultima diminuisce nella fase di allontanamento.
Il percorso compiuto annualmente dalla terra è di 940 milioni di chilometri, lunghezza — perimetro dell’ellisse — coperta in 365 giorni, 6 ore, 9 minuti circa. Dividendo pertanto il cammino compiuto per il tempo impiegato a percorrerlo avremo la velocità media della terra che è pari a 29,8 km/sec. Un km/sec = 3600 km/h. Le velocità medie dei pianeti sono quindi inversamente proporzionali alla distanza dal sole; si va cioè dai 47,90 km/sec di Mercurio ai 4,74 km/sec di Plutone.
Altri problemi interessanti derivano dalla osservazione dei pianeti e conducono, allorché consideriamo le distanze dei pianeti dal sole, a eseguire pratici e facili calcoli. Un semplicissimo calcolo per ricordare tali distanze in unità astronomiche (l’unità astronomica U. A. rappresenta la distanza media tra la terra e il sole) è stato inventato da Bode e Titius: si scrivono i numeri O e 3; dal tre in poi si continua a moltiplicare per due ottenendo una progressione. Tale progressione consta dei seguenti numeri: 0 3 6 12 24 48 96 192 384 768.
Si aggiungono poi 4 unità a ogni numero dividendo indi per 10. Si otterrà così: 0,4 0,7 1 1,6 2,8 5,2 10 19,6 38,8 77,2.
Come si è visto, confrontando tali cifre con le distanze, si vedrà che le differenze risultano trascurabili salvo che per gli ultimi due pianeti.
Il valore poi di 2,8 non è collegato a nessun pianeta che secondo la progressione dovrebbe trovarsi tra Marte e Giove.
Volendo trovare i km corrispondenti a queste distanze, si moltiplicheranno i valori trovati per 149.500.000, cifra che rappresenta la distanza media terra-sole. I valori per i pianeti sono
Caratelli a parte, ronza ancora nelle mie orecchie quella famigerata legge di Keplero per la quale: I quadrati dei tempi di rivoluzione intorno al sole sono proporzionali ai cubi delle distanze medie dal sole stesso.
Ma dovevamo parlare della massa del sole. Ora tutti sappiamo che il sole, stella che è lontana da noi circa 149.500.000 chilometri, ha un raggio 109 volte maggiore di quello della terra e ha una notevole forza di gravità.
Spostare in casa una cassa di 70 kg non è un gran problema. Ma sfido chiunque a voler spostare sulla superficie solare, fuoco a parte, una simile cassa, dato che peserebbe 2000 kg. Per calcolare la massa del sole la nostra brava professoressa di scienze, girandosi verso la lavagna, scriveva la seguente formula
nella quale F era la forza centripeta, m la massa della terra, r la distanza media dal sole e w l’angolo descritto dalla terra indipendentemente dal raggio in un tempo t. In base a questa formula, se in tale tempo t la, terra descrive un determinato angolo x, la velocità angolare è data da:
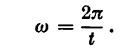
Considerato poi che un’intera rivoluzione è pari a 2, in un tempo T la velocità sarà data da:
Riprendendo ora in esame la formula e procedendo alle debite sostituzioni, considerata la forza centripeta F con la legge di Newton, si avrà
nella quale m = massa della terra, m’ = massa del sole, r = distanza media tra la terra e il sole; in base ad essa la densità del sole, cioè il rapporto tra la sua massa e il suo volume, è di 1,4.