Per circonferenza intendiamo una linea piana chiusa i cui punti abbiano tutti la medesima distanza da un punto interno detto centro.
La parte di piano limitata da una circonferenza è detta cerchio.
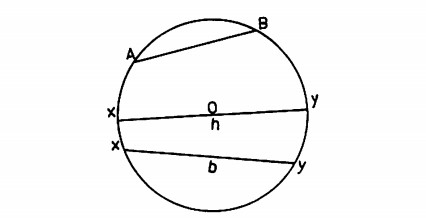
Se in una circonferenza di centro O tracciamo un segmento AB che congiunga due dei suoi punti, avremo una corda; h corda si chiamerà diametro se passerà per il centro; ogni corda che non passi per il centro è logicamente inferiore al diametro stesso. La parte di circonferenza che va dal punto A al punto B è detta arco, mentre questi due punti si chiamano estremi dell’arco. La corda AB si dice sottesa dall’arco; ne deriva quindi che archi uguali sottendono corde uguali.
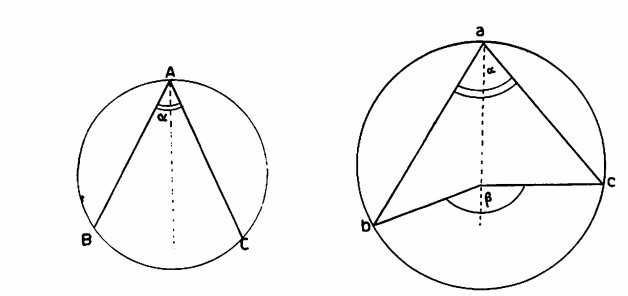
Un diametro divide la circonferenza in due semicirconferenze o se si tratta di un cerchio in due semicerchi. La parte di piano delimitata dall’arco AB e dalla corda sottesa è il segmento circolare a una base mentre la parte di cerchio limitata dal diametro e da una corda è un segmento circolare a due basi. Un angolo alla circonferenza sarà un angolo che ha il vertice in un punto della circonferenza e i lati che passano per due punti nella circonferenza stessa. Un angolo al centro sarà invece un angolo che ha il vertice nel centro di questa circonferenza.
Corrispondenti si diranno due angoli che insistono sui medesimo arco; bisogna tener presente che un angolo alla circonferenza è la metà esatta dell’angolo al centro corrispondente. Tutti gli angoli alla circonferenza che insistono sullo stesso arco sono uguali. Gli angoli iscritti in una semicirconferenza sono retti.
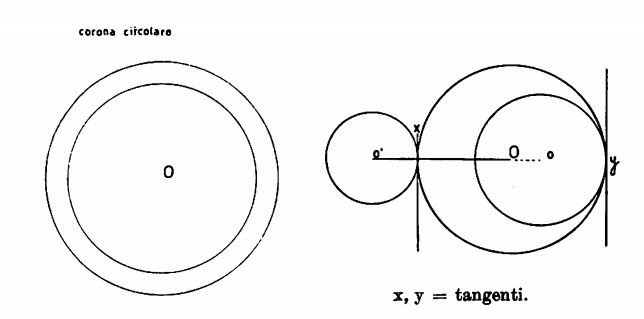
Due circonferenze si diranno concentriche allorché avranno il medesimo centro; la parte di piano tra esse compresa è detta corona circolare.
Due circonferenze si diranno tangenti esternamente quando la distanza tra i centri sarà pari alla somma dei raggi; le due circonferenze avranno pertanto un solo punto in comune (punto di contatto) attraverso il quale (vedi illustrazione) passa la tangente x.
Una figura poi geometricamente molto interessante è quella rappresentata dalla parte di piano racchiusa da un’ellisse. L’ellisse è rappresentata in natura dalla sezione obliqua del fusto di numerosi vegetali o dalle orbite descitte dai pianeti.
ellisse
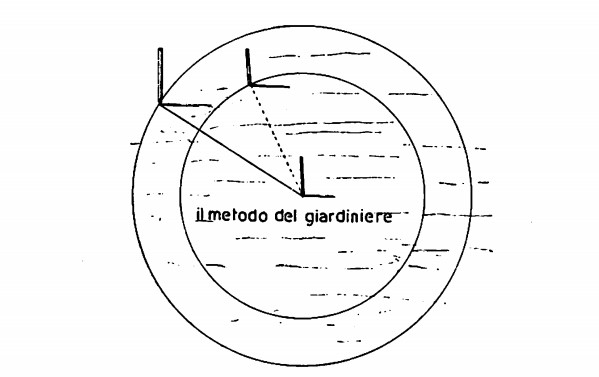
Osserviamo ora un giardiniere all’opera che costruisca delle aiuole.
Per prima cosa pianterà un pioletto al quale legherà uno spago; servendosi dello spago come raggio, traccerà sul terreno la circonferenza della futura aiuola (vedi figura).
Tale metodo fu il più usato nell’antichità per tracciare cerchi sul terreno. È chiaro che un cerchio racchiude un’area tanto più grande quanto più lunga è la sua circonferenza. Tra un cerchio piccolo e uno grande corrono le seguenti relazioni:
a) il rapporto tra la circonferenza e il raggio è pari al rapporto tra un’altra circonferenza. e il suo raggio.
b) Il rapporto tra una circonferenza e il proprio diametro è pari al rapporto che vi è tra un’altra circonferenza e il suo diametro. Infatti è costante il rapporto tra la lunghezza della circonferenza e il diametro. (Indicato con π = 3,14159265358979323846264338…)
Fin dalle scuole elementari noi sappiamo di questo rapporto costante fra il diametro e la circonferenza (3,14…). Ammesso che la Terra sia una sfera perfettamente regolare e levigata, supponiamo che l’equatore, anziché una linea immaginaria, sia un cerchio di metallo messo in giro alla Terra come il cerchio di una botte. Si tratterà di un cerchio della lunghezza di 40 milioni di metri.
Se tagliassimo in un punto questo cerchio, allargandolo ed inserendovi un tratto di circa 3 metri, avremmo portato la lunghezza del nostro cerchio a 40.000.003 metri. Ora il cerchio non aderirà più come prima alla Terra, ma si sarà formata una intercapedine. Quale sarà all’incirca la misura di questa intercapedine, cioè di quanto disterà il cerchio dalla superficie della Terra? Moltissimi risponderanno, e forse anche voi, che si potrà trattare di una piccolissima frazione di millimetro, dimostrando così di aver dimenticato l’esistenza di un rapporto fisso diametro circonferenza.
Questo rapporto come abbiamo visto è di circa 3, e quindi a ogni aumento di 3 della circonferenza corrisponde un aumento di uno del diametro. Avendo cioè noi aumentato la circonferenza di circa 3 metri, si avrà un aumento del diametro di 1 metro. L’aumento del raggio, che corrisponde all’intercapedine, sarà dunque di 50 centimetri.