In questa guida spieghiamo come si calcola l’area di un poligono regolare.
In un rettangolo l’area è data dal prodotto della base per l’altezza ed è indicata con l’espressione S = bh; si può ancora dire che la base di un rettangolo si ottiene dividendo l’area per l’altezza o ancora che l’altezza si ottiene dividendo l’area per la base.
In un quadrato invece l’area sarà data dal quadrato del lato (S =l2) per cui la lunghezza del lato si otterrà dalla radice quadrata dell’area.
Un esempio pratico sarà dato dal calcolo dell’area di un pavimento rettangolare composto da x mattonelle quadrate di lato y; è sufficiente ricavare l’area di una mattonella (y2) e moltiplicare il valore ottenuto per il numero delle mattonelle (x); il prodotto sarà l’area cercata; anche se tale pavimento non è suddiviso in mattonelle quadre, potremo sempre immaginare il pavimento diviso in quadrati (dimostrazione dell’assunto S = bh). Infatti sia un pavimento di 8 m per 12 m; l’area sarà di 96 m2, valore che si ha anche immaginando il pavimento diviso in 6 quadrati, ciascuno di lato 4 m. Infatti l’area di ogni quadrato è 16 m2; 16 • 6 = 96 m2.
L’area di un parallelogrammo è parimenti data dalla formula S = bh, poiché un parallelogrammo è equivalente a un rettangolo che abbia la stessa base e la stessa altezza; 
ci darà invece l’area del triangolo, da cui si ha che la base di un triangolo è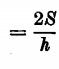 
, e quindi 
.
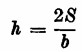Possiamo ancora trovare l’area di un triangolo conoscendo le lunghezze dei lati con la formula di Erone:
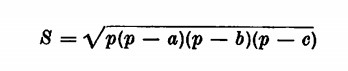
nella quale p rappresenta il semiperimetro e a, b, e, sono i lati; con questa formula è facile calcolare l’area di un triangolo che abbia, poniamo, i lati di cm 4, 6, 8. Si ha infatti
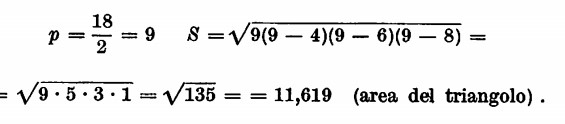
L’area del rombo e data invece da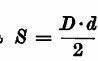 
, da cui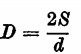 
cioè l’area del rombo è uguale al semiprodotto delle diagonali D e d, mentre una diagonale è uguale al doppio dell’area diviso l’altra diagonale.
Il trapezio avrà l’area data dal prodotto della semisomma delle basi per l’altezza
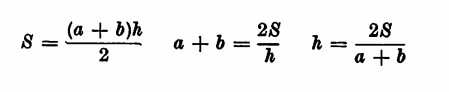
L’area di un poligono regolare è uguale al semiperimetro per l’apotema
S = pa .
Ricordiamo inoltre che nei poligoni regolari l’apotema è la perpendicolare abbassata dal centro su uno dei lati del poligono.