In questa guida spieghiamo come si costruisce la retta numerica.
Numeri interi
L’avere tolto i limiti alla eseguibilità della sottrazione ci ha portato alla costruzione dei numeri negativi.
In conseguenza di ciò, l’insieme dei numeri naturali è diventato sottodominio di un nuovo dominio, più ampio, di numeri: ora, abbiamo chiamato i numeri naturali ‘positivi’ e abbiamo riunito positivi e negativi sotto il termine comune di ‘numeri interi’.
Come abbiamo visto, i numeri naturali sono il risultato dell’attività pratica del contare: per questo motivo si sono potuti rappresentare mediante segni numerici quali fiammiferi o trattini disegnati sulla carta.
Con i numeri negativi ciò non era più possibile direttamente; tuttavia questi ultimi si sono potuti interpretare come il risultato di un particolare procedimento di cancellazione dei segni numerici che costituivano i numeri naturali.
È a questo punto che abbiamo introdotto il concetto di ‘retta numerica’. La retta numerica non è altro che una specie di scala orizzontale i cui pioli rappresentano i numeri interi

Inizialmente abbiamo interpretato questi pioli come segni numerici costituiti da fiammiferi o trattini. Lo spazio interposto tra i singoli pioli non aveva quindi nessun significato autonomo; si trattava soltanto dello spazio da porre tra segni di numeri interi diversi per motivi di carattere essenzialmente pratico, proprio come è necessario intervallare i singoli simboli costituenti le figure numeriche, per ‘tenerli distinti gli uni dagli altri’.
Frazioni sulla retta numerica
La soluzione dei casi in cui la divisione non era eseguibile senza resto ci ha portati alla costruzione dei numeri frazionari. Cosi anche l’insieme dei numeri interi è diventato un sottodominio di un nuovo dominio numerico: quello dei numeri ‘razionali’, comprendente sotto di sè quello degli interi e quello dei frazionari.
In conformità a quanto si è detto, un numero razionale è un numero che si può esprimere mediante una frazione, ovvero mediante una coppia di numeri interi. D’altra parte, anche i numeri interi si possono considerare come frazioni, ovvero coppie di numeri; in questi casi il denominatore è sempre uguale a 1
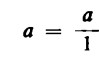
Abbiamo introdotto il concetto di retta numerica per i numeri interi. È naturale pensare che questo concetto ci possa servire per dare una rappresentazione grafica anche dei numeri razionali.
Come si può procedere?
Come abbiamo appena visto, originariamente la retta numerica era intesa come una ‘scala di fiammiferi’. Lo spazio tra piolo e piolo aveva i! mero significato pratico di ‘tenere distinti’ i singoli segni numerici.
Con l’introduzione dei numeri frazionari, dunque con l’estensione dell’insieme dei numeri interi all’insieme dei numeri razionali, il significato degli intervalli fra i pioli muta radicalmente. Tali intervalli per i numeri interi rivestono ora anche un significato per la rappresentazione dei nuovi numeri.
Chiariamo questo fatto in relazione all’esempio inizialmente esaminato a proposito del calcolo con le frazioni: la divisione 36 : 7, ovvero 39 : 7.
Possiamo rappresentare graficamente tali divisioni, non eseguibili senza resto e perciò motivanti l’introduzione dei numeri frazionari, nella maniera seguente, in modo che le righe situate in basso risulteranno incomplete:
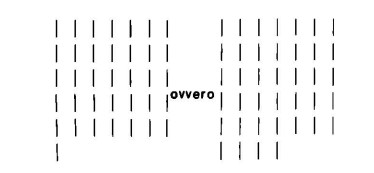
Immaginiamo ora di completare queste ultime righe, trasformandole in righe di ‘settimi’. Otteniamo la seguente figura:
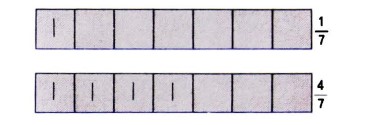
In altri termini, abbiamo costruito sette ‘caselle’ e riempito ognuna di esse con un fiammifero o un trattino, finché ce ne rimanevano a disposizione.
Il grado di ‘riempimento’ della fila di caselle, ossia il rapporto tra caselle `piene’ e caselle ‘vuote’, ci fornisce pertanto una rappresentazione grafica della suddivisione dell’unità nel processo di formazione delle frazioni.
Possiamo ora utilizzare questa figura per rappresentare sulla retta numerica i numeri frazionari.
Basta solo supporre che lo spazio tra piolo e piolo della scala che illustra la retta numerica corrisponda a una fila di caselle. Supponiamo, per esempio, di sistemare tra due pioli successivi dodici di tali caselle: allora la frazione 1/12 si può rappresentare mediante una sola casella piena, la frazione 5/12 mediante cinque caselle piene, la frazione 6/12 ovvero 1/2 mediante sei caselle piene, la frazione 4/12 ovvero 1/3 mediante quattro caselle piene, 3/12 0 1/4 con tre caselle piene, 2/3 con otto, 3/4 con nove caselle, ecc.
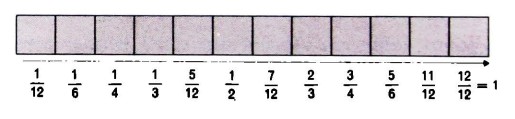
Se ora ‘smontiamo’ le caselle in modo da lasciare loro solamente la ‘base’, cioè il lato inferiore, otteniamo la seguente rappresentazione delle frazioni sulla retta numerica:

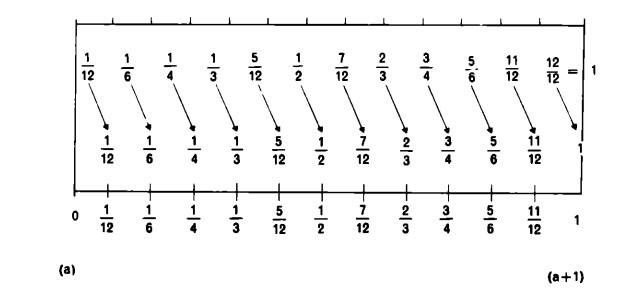
Al grafico precedente dobbiamo apportare ancora una piccola correzione: scriviamo i numeri frazionari non negli ‘spazi interni’ delle caselle ma vicino alle ‘pareti’, più precisamente in prossimità del loro limite di destra.
Il numero frazionario 1/12 non si trova, dunque, più nel mezzo della prima casella, ma alla sua estremità destra, vale a dire là ove la casella ‘finisce’. Lo stesso vale per 1/6 in riferimento alle prime due caselle, per 1/4 in riferimento alle prime tre, per 1/3 in riferimento alle prime quattro caselle, e così di seguito.
L’immagine di 1/12 (e corrispondentemente quella degli altri numeri frazionari) non coincide dunque più col fiammifero o trattino situato nel mezzo della casella, ma col punto estremo della casella:
A questo punto dobbiamo chiarire una cosa: la rappresentazione dei numeri sulla retta numerica è qualcosa di fondamentalmente diverso dalla rappresentazione dei numeri mediante segni numerici. Ponendo segni numerici all’interno delle caselle e considerando le ‘basi’ e le ‘pareti laterali’ delle caselle come rappresentazioni spaziali dei numeri frazionari, abbiamo realizzato il passo dalle operazioni con segni numerici, ancorate al mondo della prassi e appunto per questo non compromesse con l’intuizione dello spazio, a una ‘rappresentazione per immagini’, per così dire, a una ‘rappresentazione analogica’ fondata sull’intuizione dello spazio e, pertanto, in certo qual modo a una pura e semplice ‘visualizzazione’. Le dimostrazioni che faremo in seguito a partire dalla rappresentazione dei numeri sulla retta numerica avranno, dunque, un valore `analogico’; infatti, se, da una parte è vero che rappresentiamo i numeri sulla retta numerica, deve comunque rimanere chiaro che i tratti che suddividono la retta numerica sono qualcosa di completamente diverso dai segni numerici con i quali abbiamo finora operato.
Se vogliamo rappresentare i numeri frazionari sulla retta numerica, dobbiamo dunque inserire dei ‘pioli tra pioli’, dobbiamo dividere cioè gli intervalli, che finora erano quelli unitari e rappresentavano i numeri interi. Un esempio di tale suddivisione può essere la riga millimetrata o il termometro per misurare la febbre, il quale si differenzia dal normale termometro per temperature d’ambiente proprio perché sulla sua scala sono riportati accanto ai gradi anche i decimi di grado.
È inevitabile che l’immagine dei ‘pioli tra pioli’ metta in moto la nostra fantasia. Se è vero che fra i pioli già a disposizione se ne possono mettere dei nuovi, è possibile iterare di continuo questo processo? In altri termini, è sempre possibile, dati due pioli qualsiasi, porne uno nuovo tra essi ?
In effetti ciò è possibile. Questo risultato, intuitivamente plausibile se pensiamo alla retta numerica nello spazio, ma appunto per questo altrettanto dubitabile come tutti i dati ‘intuitivi’, si può dimostrare in maniera assolutamente rigorosa e sicura mediante i calcoli.
Consideriamo innanzitutto le frazioni 1/3 e 1/2 . Possiamo inserire tra questi due numeri frazionari un ulteriore numero frazionario? Evidentemente sì. Basta trasformare le due frazioni in 4/12 e 6/12; è ovvio che tra le due si può inserire la frazione 5/12 . E tra 5/12 e 6/12 possiamo inserire un nuovo numero frazionario? Analogamente a quanto abbiamo fatto prima, trasformiamo le frazioni in 10/24 e 12/24. Anche in questo caso si può inserire una nuova frazione tra le due date. Essa è infatti 11/24
11/24 e 12/24 si possono poi trasformare in 22/48 e24/48 e, di conseguenza, anche tra di esse si può inserire la frazione 23/48
Già da questo esempio si può ricavare il seguente risultato: date due qualsiasi frazioni, è sempre possibile trovarne un’altra che sta tra le prime due. Nel caso poi in cui i denominatori sono uguali e i numeratori sono numeri naturali di cui uno è l’immediato successore dell’altro, basta trasformare espandendole, le frazioni e si ha così subito un numero intermedio per un nuovo numeratore.
Il nostro procedimento si basa dunque sul principio che le frazioni si possono ‘espandere’ a piacere, vale a dire che numeratore e denominatore si possono ingrandire a piacere.
Dal momento, infatti, che il numeratore e il denominatore sono numeri naturali, abbiamo a disposizione la successione infinita e ininterrotta dei numeri naturali.
Il principio dell’infinito potenziale qui si applica, per così dire, verso l’interno: più cresce il denominatore di una frazione e sempre più vicini fra loro risultano i numeri frazionari che otteniamo – e, d’altra parte, questo procedimento consistente nel ‘porre un nuovo piolo tra due altri preesistenti non ha mai fine.
Ciò diventa naturalmente molto chiaro, se scegliamo la seguente semplicissima successione di frazioni: incominciamo con 1/2, dopodiché dimezziamo questa frazione e le successive che si ottengono una dopo l’altra senza interruzione:
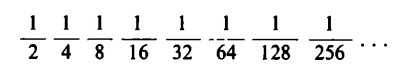
Visto che possiamo raddoppiare senza limite i numeri naturali, possiamo continuare a dimezzare senza limite anche le frazioni che di volta in volta in tal modo si ottengono.
Questo processo non può mai giungere alla fine, dal momento che esiste sempre un numero che è il doppio di un altro già dato: per ottenere tale numero doppio, non dobbiamo far altro che riscrivere ancora una volta uno dopo l’altro tutti i trattini già segnati sulla carta.
Il processo ininterrotto di suddivisione per due, raffigurato sulla retta numerica, si presenta di conseguenza così
Quello che qui salta immediatamente agli occhi è ‘l’addensarsi verso lo zero’ dei numeri frazionari; quanto più grande diventa il denominatore, tanto più piccolo diventa il numero frazionario, e un numero inconcepibilmente grande produce un numero altrettanto inconcepibilmente piccolo `sul limite sinistro’ della nostra ‘scala’. Ma questo numero non può mai diventare zero, dal momento che nel denominatore esiste sempre un numero per il quale si può dividere.
Come non esiste un ‘infinitamente grande’, così non esiste un ‘infinitamente piccolo’. Esistono soltanto, da un lato, numeri molto grandi e, dall’altro, numeri molto piccoli.
