In questa guida spieghiamo cosa sono i numeri immaginari.
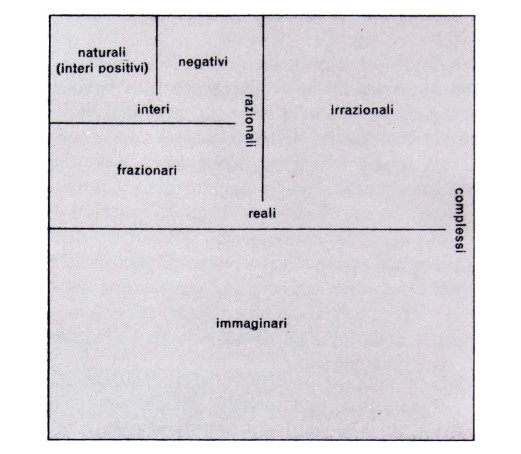
I termini ‘numero positivo’, ‘numero intero’, ‘numero razionale’ suggeriscono l’idea che esistano anche numeri ‘negativi’, ‘frazionari’, ‘irrazionali’. Analogamente anche il termine ‘numero reale’ suggerisce l’idea che esistano, forse, persino ‘numeri non reali’.
In effetti, possiamo allargare ancora una volta il dominio dei nostri numeri.
Come sempre, questo ampliamento ha luogo per rendere in ogni caso eseguibile una operazione che altrimenti non lo sarebbe. Cosi abbiamo fatto per i numeri negativi, per quelli frazionari e per quelli irrazionali.
L’ampliamento del dominio numerico che ci accingiamo a realizzare è legato all’operazione dell’estrazione di radice.
Dal momento che non tutti i numeri naturali sono quadrati, abbiamo dovuto trasformare ‘ad arte’ tali numeri naturali in quadrati sfruttando il concetto di numero irrazionale.
Ora esiste però un ulteriore gruppo di numeri che non possono essere ‘per essenza’ dei quadrati: questi sono i numeri negativi.
Siccome infatti ‘meno’ per ‘meno’ dà ‘più’, ogni numero negativo moltiplicato per sè stesso dà un numero positivo. -a per -a è sempre +a2, mai – a2; infatti – a2 è il risultato di + a per — a o di – a per + a. Questi prodotti non sono però dei quadrati, dal momento che nell’eseguire una moltiplicazione non possiamo prescindere dal segno e, di conseguenza, – a e + a non possono essere considerati ‘lo stesso numero’.
Pertanto non esiste nessun numero che moltiplicato per sé stesso dia come risultato – a. Né – 1, né – 4, né – 9, ecc. sono dunque quadrati.
Anche nel dominio dei numeri negativi possiamo tuttavia togliere ogni restrizione all’eseguibilità dell’estrazione di radice. Basta fissare che la radice di un numero negativo sia uguale alla radice del corrispondente numero positivo moltiplicata per un fattore i, I’unità immaginaria. In tal modo si ottengono i ‘numeri immaginari’: √-1 è perciò = i, √-4 = 2i, √-9 = 3i, √2 = i √2, ecc.
A tali numeri immaginari si può dare facilmente anche una rappresentazione grafica: se per rappresentare i numeri reali abbiamo usato il continuo a una sola dimensione, cioè la retta numerica disposta orizzontalmente da sinistra verso destra, per i numeri immaginari possiamo usare la seconda dimensione, cioè una retta numerica disposta verticalmente.
Come poi abbiamo unificato i numeri negativi e naturali nell’insieme dei numeri interi, i numeri interi e frazionari nell’insieme dei numeri razionali e, infine, i numeri razionali e irrazionali nell’insieme dei numeri reali, così possiamo chiamare l’insieme che comprende sia i numeri reali sia quelli immaginari insieme dei numeri complessi.