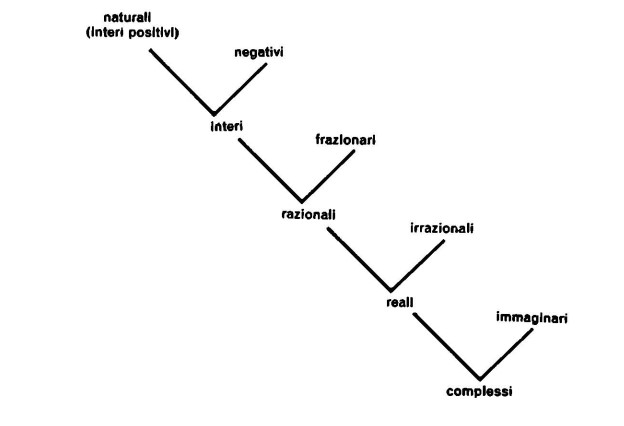
La costruzione del nostro sistema numerico, comprendente numeri reali e numeri immaginari, si fonda sul presupposto che gli unici numeri ‘naturali’ siano i numeri interi positivi con l’esclusione dello zero, e che tutti gli altri numeri non siano che delle costruzioni ‘artificiali’, ottenute a partire dai numeri ‘naturali’.
Ora, un lettore dotato di senso critico può obiettare che la stessa costruzione del sistema numerico ha in sé già qualcosa di ‘artificiale’. E questo perché nella natura, come essa ci si presenta, non ci si imbatte mai in numeri interi positivi. Una pietra, ad esempio, un foglio, un ramo spezzato, un animale, uno stagno e così via, hanno certo delle dimensioni. Tuttavia è altamente improbabile che un oggetto della natura misuri ‘esattamente’ 1 mm, 2 cm, 30 cm, 4 m, ecc. I valori numerici ‘naturali’ sono dunque quelli ‘non interi’. Di conseguenza, il continuo delle misure degli oggetti naturali dovrebbe essere il vero punto di partenza, mentre dovrebbe risultare in realtà del tutto artificiale la costruzione del sistema numerico basata sui numeri naturali. La costruzione del sistema numerico dovrebbe perciò partire dalla retta numerica e da essa dovrebbero essere poi ricavati tutti gli enti matematici.
Per quanto intuitiva sembri a prima vista tale obiezione, essa è facilmente confutabile ad una analisi più rigorosa. Infatti, per poter misurare un oggetto naturale e per poter in generale pronunciare un giudizio sulla sua lunghezza ecc., dobbiamo avere già a disposizione una ‘unità di misura’. È indifferente che questa unità di misura sia la lunghezza di 1 cm, di 1 pollice, di 1 piede, di 1 braccio ecc.; è comunque necessaria un’unità, mediante la quale misurare tutte le altre estensioni. Ora, questa unità è il primo numero naturale ‘uno’, cioè quel numero che abbiamo costruito col nostro primo fiammifero, sassolino o trattino.
Per poter effettuare delle misure nel ‘continuo’, dobbiamo fissare un certo tratto unitario. Questo tratto Io dobbiamo innanzitutto riprodurre (numeri interi); in secondo luogo, suddivideremo le singole unità così riprodotte in sotto unità, come nel caso della riga con i suoi tratti indicanti i centimetri e quelli più piccoli indicanti i millimetri. Non si può dunque misurare la ‘lunghezza naturale’ di un foglio senza aver scelto un’unità di misura.
Il continuo spaziale necessita, perciò, per la sua scomposizione di un sistema numerico come quello da noi costruito, a partire dal dominio discontinuo dei numeri naturali e procedendo passo passo fino al dominio continuo dei numeri reali.