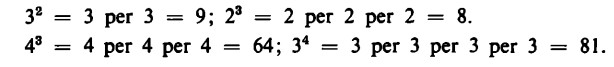In questa guida spieghiamo quali sono le proprietà delle potenze e vediamo come eseguire il calcolo.
Indicando una moltiplicazione, non facciamo che scrivere, in forma abbreviata, un’addizione; scrivendo infatti 5 • 5 la somma che noi sottintendiamo è 5 + 5 + 5 + 5 + 5. A questo punto dobbiamo fare la stessa considerazione a un livello più alto. La questione da porre è la seguente: esiste un’operazione corrispondente alla moltiplicazione dello stesso fattore ripetuta più volte, così come la moltiplicazione è una addizione dello stesso numero ripetuta più volte? In effetti questa operazione esiste.
Così come siamo passati da
(a + b + c + . . .) ad (a + a + a + a +… = n per a),
possiamo ora passare anche da
(a per b per c per …) ad (a per a per a per a per …).
Siccome poi abbiamo a disposizione un metodo per rappresentare graficamente o, per meglio dire, nello spazio e nel tempo la moltiplicazione con tre fattori, non è difficile capire come te moltiplicazioni con lo stesso fattore non siano altro che un caso speciale della moltiplicazione con più fattori diversi.
La figura che rappresenta il prodotto a per a è naturalmente un rettangolo. Però, dal momento che il numero delle righe coincide con il numero delle colonne, si tratterà di un rettangolo speciale, ossia di un quadrato.

È questo il motivo per cui il numero risultante dalla moltiplicazione di un numero per sé stesso si dice ‘quadrato’.
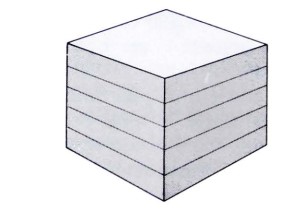
In modo analogo, la figura che rappresenta un numero moltiplicato tre volte per sé stesso, a per a per a, è un parallelepipedo e, anzi, un caso
particolare di parallelepipedo, cioè un cubo, poiché i suoi spigoli sono tutti di lunghezza uguale.
Corrispondentemente si dice `cubo’ un numero moltiplicato tre volte per sé stesso. Inoltre, esattamente come, per ragioni di brevità, esprimiamo la ripetizione di addendi uguali
a, a + a, a + a + a, a + a + a + a, . . .
mediante
a, 2a, 3a, 4a, . . , n . a,
così esprimiamo la ripetizione di fattori uguali
a, a per a, a per a per a, a per a per a per a,…
scrivendo una sola volta il numero a e ponendo in alto come indice superiore il numero che dichiara quante volte il fattore a viene moltiplicato per sé stesso, ossia
Inoltre, allo stesso modo che chiamiamo prodotto la somma di addendi uguali, indichiamo anche il prodotto di fattori uguali con una nuova parola: potenza.
Consideriamo ora l’espressione ab = c, che significa a preso come fattore b volte dà per risultato c; a si dice base (numero di base), b si dice esponente (numero che sta in alto) — oppure, come vedremo tra poco, anche logaritmo — c, poi, si dice potenza.
Ancora un’osservazione: come per la moltiplicazione con più di tre fattori, anche per l’elevazione a potenza superiore al cubo, non possiamo fornire una costruzione geometrico-spaziale adeguata. Infatti nell’elevazione a potenza ogni ‘fattore’ in più richiede una nuova dimensione spaziale, mentre abbiamo a disposizione solo tre dimensioni.
Risulta qui chiaramente come molte volte in matematica il significato dei concetti sia svincolato dai dati dell’esperienza, per cui, molto spesso, a quelli non è possibile dare una adeguata rappresentazione spaziale. Il nostro metodo di costruzione dei numeri mediante segni numerici, ad esempio, ci permette di dare una rappresentazione spaziale del concetto di numero alla prima potenza, di quadrato o di cubo, ma non è più sufficiente per numeri elevati alla quarta potenza — per non parlare, poi, della quinta potenza o di potenze superiori.
Come per l’addizione e per la moltiplicazione, anche per l’elevazione a potenza è ovvio chiedersi se valga la legge della commutatività; in altri :ermini, come a + b coincide con b-i-a e a per b coincide con b per a,
vale ora anche ab = ba? Moltiplicare, cioè, il fattore a per b volte coincide con il moltiplicare il fattore b per a volte?
Come già traspare dalla disposizione asimmetrica dei termini nell’elevazione a potenza, la proprietà commutativa non vale. Visto che, poi, una legge matematica — supposto che valga — deve valere senza eccezioni, la dimostrazione della non-commutatività dell’elevazione a potenza si può ottenere con estrema facilità; è sufficiente esibire un solo controesempio
In conclusione, occorre ricordare che:
a) qualsiasi potenza di 1 è uguale a 1;
b) qualsiasi potenza di 0 è uguale a 0;
e) elevando un numero qualsiasi alla potenza 0 abbiamo per risultato 1;
d) elevando un numero qualsiasi a esponente 1, il numero non varia;
e) una potenza di 10 la si esegue facendo seguire l’unità da tanti zeri quanti indicati dall’esponente;
f) la potenza di un numero decimale ha tante cifre decimali quanto è il prodotto delle cifre decimali della base per l’esponente;
g) il prodotto di due o più potenze che hanno uguale base è una potenza che ha la stessa base e come esponente la somma degli esponenti;
h) il quoziente di due potenze che hanno la stessa base è una potenza avente la medesima base e come esponente la differenza degli esponenti;
i) la potenza di una potenza è uguale a una potenza che ha come base la stessa base e come esponente il prodotto degli esponenti.
Cerchiamo ora di spiegare in pratica ciò che è stato detto; sia ad esempio da elevare a potenza un numero decimale, come 1,72 (caso f): 1,712 = 2,89; il caso g significa che se dobbiamo eseguire un prodotto come 52 • 53 potremo scrivere: 55 (infatti 53+2 = 55).