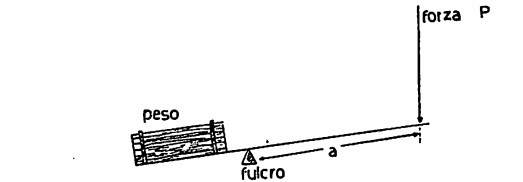
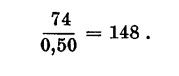Una sbarra rigida girevole intorno a un punto fisso (fulcro): questa è la leva. Essa è in equilibrio quando l’insieme delle forze ad essa applicate soddisfa determinate condizioni.
Se si hanno due forze perpendicolari alla sbarra che abbiano intensità P e Q, la leva starà in equilibrio quando queste forze vengono applicate in modo tale che P•a = Q•b, nella quale a e b rappresentano le distanze dal fulcro.
Tutti ricordiamo la celebre frase d’Archimede: «Datemi un punto d’appoggio e vi solleverò il mondo o. La mia forza posso applicarla su di una leva a una distanza dal fulcro tale che il prodotto (P• a) risulti uguale a quello (Q•h) dovuto al peso della terra. Per mezzo di una leva infatti — astrazione fatta dal paradosso d’Archimede —possiamo sollevare, anche esercitando la pressione con una sola mano, pesi di 1500 kg purché il braccio della leva abbia lunghezza conveniente.
Supponiamo che si debba sollevare un quintale collocato a 90 cm dal fulcro; la forza necessaria a sollevarlo potrà essere di 30 kg.
Infatti se P•a.Q•b, P•a 100 • 90 = 9000 (1 q = 100 kg). Tale forza dovrà essere applicata a una distanza dal fulcro di:
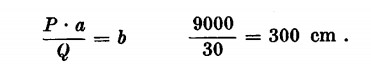
La nostra forza dovrà quindi agire a una distanza di 3 metri dal fulcro.
Osserviamo un fluido in equilibrio e constatiamo la proporzionalità esistente tra profondità e pressione. In un liquido fermo, infatti, tutti i punti aventi lo stesso livello hanno la stessa pressione. La formula che ci dà la misura di tale pressione è la seguente:
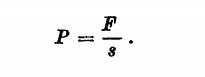
Blaise Pascal fece un’interessante applicazione di tale principio: il torchio idraulico.
Lo schema di un torchio idraulico può esser compreso immaginando due recipienti cilindrici di diverso diametro collegati tra loro da un condotto alla base. Se tramite un pistone comprimiamo il liquido nel cilindro minore avremo una spinta proporzionalmente superiore esercitata dal liquido nell’altro cilindro.
Se ci servissimo di un torchio idraulico sarebbe sufficiente esercitare sul cilindro minore, supponendo che quest’ultimo abbia una superficie di 100 cm2, una pressione di poco superiore ai 10 kg per sollevare una tonnellata, posta su di una superficie di 10.000 cm2 (1 m2).
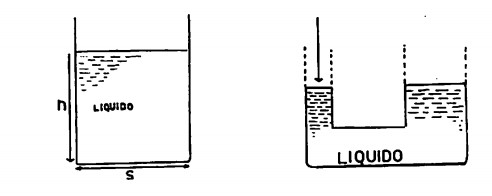
La pressione esercitata dal peso di 10 kg sarà:
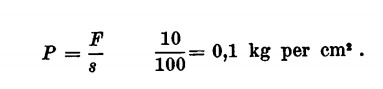
E così pure quella esercitata dalla tonnellata; infatti:

Un’interessante esperienza sulla pressione dei liquidi è quella detta della botte di Pascal. Si prendono due botti a perfetta tenuta e si riempiono d’acqua. Esternamente a una di esse si applica in modo che comunichi con l’interno un tubo rigido del diametro di 10 cm disposto in posizione verticale; alla seconda si applica invece, nello stesso modo, un tubo del diametro di cm 1. Si comincia poi a riempire d’acqua il tubo di diametro maggiore, fino a quando l’acqua, raggiunta in esso una certa altezza, provocherà lo scoppio della botte. Se poi riempiamo d’acqua anche il tubo più sottile, collegato con la seconda botte, noteremo che lo scoppio di questa avverrà quando l’acqua avrà raggiunto nel tubo la stessa altezza a cui era arrivata nel primo, pur avendo ovviamente usato nella seconda esperienza una quantità d’acqua molto minore. Ciò è dovuto al fatto che la pressione che si esercita su tutta la superficie interna delle botti non è dovuta. alla quantità di acqua che vi preme ma all’altezza che il liquido raggiunge.
Iniziando questo paragrafo ci siamo ancora una volta imbattuti nel nome di Archimede, il quale fu il primo a fare oggetto delle proprie osservazioni le condizioni di equilibrio di una leva; una leva è una macchina basata sui principi fondamentali della statica e il suo funzionamento è quanto mai semplice e comprensibile.
Archimede però trattò anche delle pressioni dei liquidi nella sua opera sui galleggianti. Soprattutto si occupò della stabilità delle navi e sua è la legge secondo la quale un corpo immerso in un liquido riceve una spinta dal basso verso l’alto pari al peso del liquido spostato. Poiché ogni liquido contenuto in un qualsiasi recipiente preme sulle pareti del recipiente stesso con una forza che è perpendicolare in ogni punto alla parete, avremo che la pressione, ovvero questa forza, sarà data dalla formula già vista
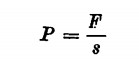
nella quale s è l’area della superficie e F è la forza complessiva.
Per unità di pressione si intende un chilogrammo per centimetro quadrato; l’atmosfera, ad esempio, esercita 1,033 kg/cm, di pressione, al livello del mare. Il principio di Pascal afferma come i liquidi trasmettano in ogni senso le pressioni esercitate sulla loro superficie, con uguale intensità. Volendo esemplificare consideriamo una piccola superficie piana ovvero il fondo di un recipiente in cui vi è un liquido di determinato peso specifico. La forza con la quale il liquido preme sulla superficie stessa è data dalla formula:
![]()
nella quale F è la forza, H l’altezza del liquido, d la densità, s la superficie.
Possiamo anche dire che
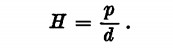
Questi e altri principi sono alla base del calcolo delle pompe idrauliche. Chiariamo prima alcuni concetti; per portata di una corrente, cioè di una massa liquida in movimento, si intende il volume del liquido misurato solitamente in m3 che passa in ogni minuto secondo attraverso una sezione trasversale.
Il teorema di Bernoulli ci dice che in ogni punto della corrente a regime permanente (cioè una corrente nella quale la velocità e la pressione si mantengono in ogni punto e in ogni momento costanti) è costante la somma dell’altezza relativa alla velocità, dell’altezza relativa alla pressione e dell’altezza geometrica. Per altezza relativa alla velocità si intende l’altezza alla quale giungerebbe nel vuoto un grave lanciato verticalmente in alto, a velocità v; per altezza relativa alla pressione si intende quella alla quale arriverebbe un liquido in un tubo aperto alle due estremità e posto al centro della corrente; per altezza geometrica infine si intende l’altezza del centro della sezione rispetto a un piano orizzontale di riferimento.
Portata di una pompa sarà invece il volume di liquido in m3 che viene sollevato a ogni secondo. Una pompa manda un liquido da un punto a un altro, in genere da un livello inferiore a uno superiore. Per prevalenza statica si intende la distanza verticale tra i due livelli (di aspirazione e di mandata). Se la prevalenza si indica con H, con Q la portata, con d il peso specifico, con N, la potenza teorica che serve per far funzionare la pompa (espressa in cavalli) si ha:
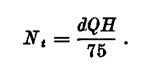
Facciamo un esempio pratico: una pompa è messa a riempire un serbatoio situato a 50 m con 400 m3 di acqua all’ora. Causa notevoli perdite meccaniche e idrauliche, il rendimento della macchina è del 50%; se volessimo conoscere la potenza in cavalli occorrente a muovere la pompa, avremmo che 400/3600 ci dà la portata in m3/sec, cioè 0,111.
La potenza teorica è data dal peso specifico dell’acqua uguale a 1000 kg al m3 moltiplicato l’altezza (50 m) e la portata (0,111 m3) diviso 75.
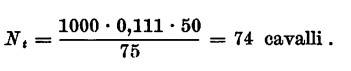
La potenza effettiva da utilizzare sarebbe però maggiore tenuto conto delle perdite