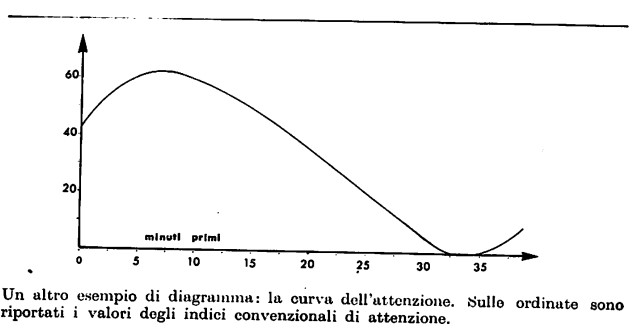
In questa guida spieghiamo come costruire e leggere i diagrammi.
Tutti noi abbiamo visto dei diagrammi: come continuamente riportati nei giornali, che ci dicono qual è la distanza necessaria per fermarsi ad una data velocità della nostra macchina.
Per capire bene i diagrammi, dobbiamo partire un po’ da lontano, utilizzando gli esempi che abbiamo riportato. Consideriamo il diagramma che ci dà la distanza necessaria per fermarci: la nostra esperienza ci ha insegnato che questo spazio aumenta con l’aumentare della velocità, cioè che, se freniamo bene, distanza e velocità non sono due cose indipendenti, ma sono legate fra di loro da una legge precisa; in matematica si dice che una è funzione dell’altra.
Questa legge può essere anche ricavata teoricamente, tenendo conto di tutte le caratteristiche delle nostre macchine, ma molto più semplicemente può essere ricavata da una serie di prove sperimentali.
Trovato un tratto di strada di campagna dritta e senza traffico, lanciate la macchina ad una certa velocità, fermate bruscamente fino al limite del blocco delle ruote, quindi misurate la lunghezza delle strisce di gomma sull’asfalto, servendovi di un metro o dei vostri passi (è utile conoscere la lunghezza del proprio passo, in genere tra i 60 e i 70 cm). Tale lunghezza ci dà lo spazio di frenata. A questa distanza si deve aggiungere quella percorsa nel tempo che trascorre da quando la vostra mente decide di frenare e quando iniziate la frenata vera e propria: il tempo di « riflettere ». Ci sono apparecchi per misurare il tempo di reazione, prendiamo un valore medio di 10 di secondo; allora, come si è visto quando abbiamo parlato della velocità, lo spazio percorso senza frenare (in metri) = tempo di riflesso (in sec) per la velocità dell’auto (in metri al sec); il nostro contachilometri ci dà la velocità in km (km/ora); per passare
ai metri al sec (m/sec) basta moltiplicare per mille (1 km = 1000 m) e dividere per 3600 (un’ora = 3600 sec) cioè

Ripetiamo le nostre frenate e i nostri calcoli per diverse velocità e otteniamo ad esempio la tabella seguente

Questa tabella ci dà un’idea di come aumenta lo spazio all’aumentare della velocità, ma ciò non lo si vede subito: dobbiamo eseguire mentalmente la differenza. Così se vogliamo sapere qual è lo spazio necessario per fermarsi a 50 km/ora, la tabella ci dice solo che sarà compreso fra i 17,8 e i 37,4 metri, circa a metà fra i due valori,
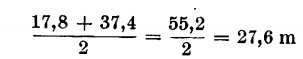
evidentemente è necessario fare un diagramma, in quanto si tratta non di un valore esatto, ma approssimativo.
Prendiamo due rette ortogonali, che chiameremo assi del diagramma, quello orizzontale sarà l’asse della velocità dell’auto e quello verticale l’asse degli spazi di frenata.
Lungo questi assi riportiamo una graduazione, la divisione in mm, o in cm, o in una scala qualsiasi, secondo le dimensioni del diagramma, facciamo poi corrispondere ad ogni intervallo della graduazione, un certo intervallo delle « cose » (in matematica, si dice grandezze) in discussione. Ad esempio, un cm di scala corrisponde a 10 km/ora, o, il che è lo stesso, un mm di scala corrisponde a 1 km/ora; lungo l’altro asse, quello degli spazi di frenata, un mm di scala corrisponde a 2 metri cioè 1 cm di scala è pari a 20 metri.
I due assi diventano così due assi coordinati, perché ad ogni punto di essi corrisponde un unico e definito valore delle grandezze rappresentate su quell’asse; questo valore si chiama la coordinata di quel punto.
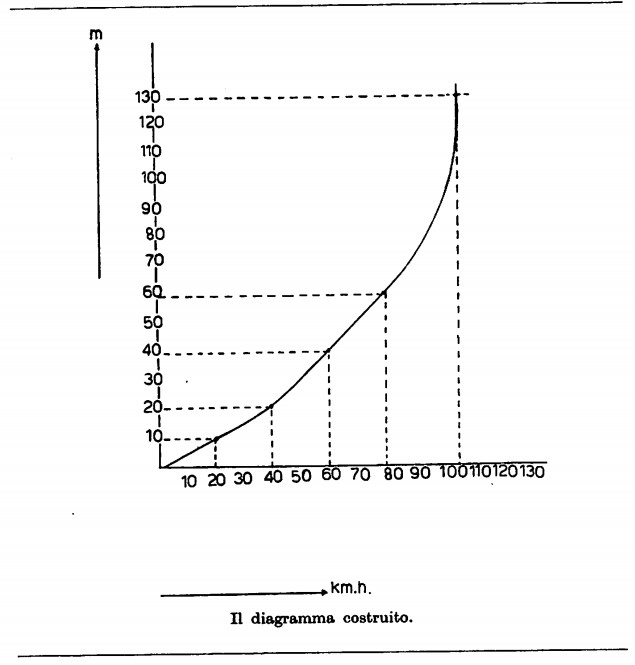
I due assi ortogonali si chiamano anche cartesiani, dal nome del matematico Cartesio. Immaginiamo ora di tracciare per ogni punto <lei due assi una retta ortogonale all’asse stesso. Lo spazio compreso fra i due assi diventa allora una specie di reticolato ed ogni punto è individuato dalle due rette ortogonali che passano per esso; queste due rette incontrano gli assi in due punti, lo coordinate di questi due punti sono le coordinate del punto del piano. Il piano così fatto diventa un piano coordinato o piano cartesiano.
Nella figura sono state tracciate, per non rendere confuso il diagramma, solo alcune rette coordinate relative ai km/ora e a ogni 20 metri di distanza di frenata; ad esempio il primo punto indicato è dato dall’attraversamento dalle rette di coordinate velocità

= 20 km/ora e distanza = 10 metri; questi due valori sono le coordinate del punto in oggetto.
Riportiamo adesso sul piano cartesiano alcuni punti relativi alle prove di frenata; se abbiamo fatto sei prove avremo sei punti; le coordinate di questi punti sono date dalle tabelle; ad esempio: velocità = 80 km/ora distanza di frenata = 60 m;
individuano il terzo punto.
Vediamo subito dal diagramma che i punti si susseguono con regolarità; questo conferma quanto avevamo detto prima, cioè l’esistenza di una legge precisa che lega i valori della velocità con i valori delle distanze di frenata.
Possiamo perciò collegare i punti tra di loro, con una curva tratteggiata, nel nostro caso, in modo che si ottenga con continuità, sul diagramma, la rappresentazione della relazione fra le due grandezze in argomento.
È ora possibile per un qualsiasi valore di una delle due grandezze trovare immediatamente l’altra corrispondente, basta muoversi lungo la retta coordinata corrispondente fino ad intersecare la curva, ruotare poi di 900 e seguendo la retta coordinata ad essa ortogonale andare a leggere il valore sul relativo asse coordinato; se voglio sapere quanto spazio occorre per frenare a 80 km/ora, leggo 80 km/ora sull’asse delle ascisse, innalzo la perpendicolare, retta punteggiata che incontra la curva in un punto; tracciando la parallela all’asse delle ordinate si incontra l’asse coordinato della distanza e si legge la coordinata distanza = 60 metri.
Abbiamo così imparato a costruire un diagramma e a leggerlo.