Il compenso a cui ha diritto chi cede ad altri l’uso di un capitale in denaro si chiama interesse.
Se depositate in una Banca una somma, vi verrà corrisposto un compenso, che sarà tanto più grande quanto maggiore sarà la cifra depositata e la durata del deposito. Questo compenso è appunto l’interesse che sarà calcolato a un tanto per cento; vi saranno date ad esempio nel caso del 5% (cinque per cento) annuo, 5 euro per ogni 100 euro che verranno lasciate in deposito per un anno.
Possiamo quindi già ricavare alcune utili formule. Se indichiamo con C il capitale, con r il tasso annuo unitario (nel caso del 5% il tasso unitario sarà 0,05) e con t il tempo espresso in anni, l’interesse I sarà uguale a:
I = C x r x t.
Ad esempio, un capitale di Euro 15.000 depositato per tre anni all’interesse del 5% annuo frutterà:
15.000 x 0,05 x 3 = Euro 2.250 .
L’interesse, anziché per anni, può anche essere calcolato per mesi o per giorni. Nel primo caso il tempo t sarà espresso in mesi e l’interesse dovrà essere diviso per 12. Avremo:
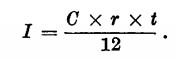
E nel caso di t espresso in giorni:
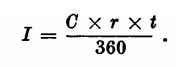
Il denominatore è 360 in quanto l’anno commerciale viene generalmente calcolato di 360 giorni (12 mesi di 30 giorni).
Esempio: Quanto ci verrà accreditato per interessi, se abbiamo depositato in Banca per 100 giorni Euro 25.000 al 4%
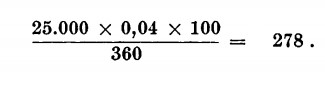
Quello che abbiamo visto è il calcolo dell’interesse semplice. In verità, se depositate una somma in Banca come nel primo esempio, vi verrà corrisposto alla fine dei tre anni un interesse un poco maggiore, per il fatto che ad ogni fine di anno gli interessi maturati vengono capitalizzati, vanno cioè ad aumentare il capitale, fruttando a loro volta interessi nell’anno successivo. Questo modo di calcolare gli interesse prende il nome di interesse composto.
Di questo parleremo un poco più avanti. Vediamo ancora qualcosa sull’interesse semplice.
Dalla nostra formula I = C • r • t, molto facilmente possiamo ricavare le altre formule che ci danno il capitale impiegato, il tasso oppure il tempo:

La somma del capitale più l’interesse capitalizzato prende il nome di montante. Se indichiamo il montante con M possiamo
scrivere che:
M = C + I
ed essendo I = C•r•t avremo:
M = C + Crt
e ricordandoci del raccoglimento a fattore comune:
M = C(1 + rt).
Esempio: Calcolare il montante di una somma di Euro 100.000 depositata per 10 anni al 3%.
100.000(1 + 0,03 x 10) = 100.000 x 1,3 = 130.000 .
Vediamo ora invece come si calcola l’interesse composto. Chiamando C il capitale iniziale, il montante dopo il primo anno sarà dato da:
M1 = C + Cr = C(1 + r).
Dopo il secondo anno il montante sarà:
M2 = C(1 + r)(1 + r) = C(1 + r)2 .
Dopo n anni sarà quindi
Mn = C(1 + r)n .
Esempio: Calcolare il montante di un capitale di Euro 40.000 impiegato per 4 anni all’interesse composto del 6%.
40.000(1 + 0,06)4 = 40.000 • 1,2625 = 50.500 euro.
Dalla formula M = C(1 + r)n possiamo ricavare quella che ci dà l’interesse composto:
I = C[(1 + r)n — 1] .
Esempio: Quale sarà l’interesse composto (capitalizzazione annuale) che ci dà un capitale di Euro 28.000 per 15 anni al 5%
28.000[(1 + 0,05)15 — 1] = 28.000(2,079 — 1) = Euro 30.212
Il capitale si è quindi più che raddoppiato.