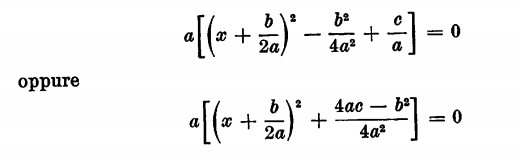Un’equazione di secondo grado si presenta nella forma ax2 + bx + c = 0; in essa l’incognita è la variabile x mentre le le lettere a, b, c, sono numeri noti.
Condizione:
a ≠ 0.
Iniziamo dal caso c = 0. L’equazione assume allora la forma
ax2 + bx = 0, [oppure x(ax + b) = 0].
Se x = 0 (oppure ax + b = 0) tale prodotto diventa nullo;
quindi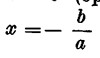 
e naturalmente l’equazione ammetterà le due soluzioni e cioè x’ = 0 e 
.
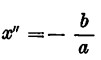Se b = 0, l’equazione assume la forma ax2 + c = O. Questa equazione può anche scriversi nella seguente forma
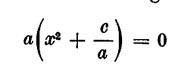
Il coefficiente a non è nullo: il prodotto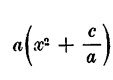 
diventa nullo alla condizione che anche x2 + c/a sia nullo.
In particolare consideriamo il caso in cui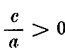 
; l’equazione in questo caso non ammette soluzioni.
Se c = 0 l’equazione assume. la forma x2 = 0 (ammette allora due soluzioni uguali e coincidenti, soluzione per x = 0).
Vediamo adesso il caso contrario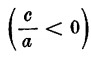 
. Si avrà allora la forma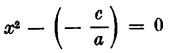 
Quest’espressione possiamo scriverla
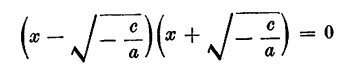
Avremo pertanto le due soluzioni
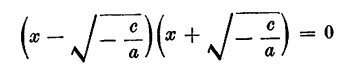
Se si fa invece l’ipotesi che b e c non siano nulli, avremo la scrittura
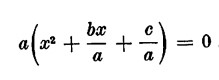
L’equazione potrà scriversi
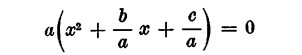
ma 
non è che l’inizio dello sviluppo del quadrato di
Potremo allora scrivere
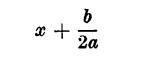
Se 4ac — b2 è maggiore di zero, (4ac — b2/sup>) > 0, la parentesi che contiene il quadrato positivo o nullo sommato alla quantità positiva
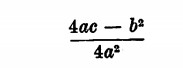
risulta positiva. Il suo prodotto per a non può pertanto essere nullo e l’equazione non ha alcuna soluzione.
Se invece 4ac — b2 = 0 l’equazione verrà scritta nella forma
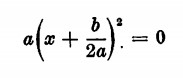
e il primo membro risulterà nullo a condizione che
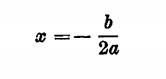
questa è la sola risoluzione dell’equazione stessa.
Se invece 4ac — b2 risulta minore di 0 l’equazione risulta della forma
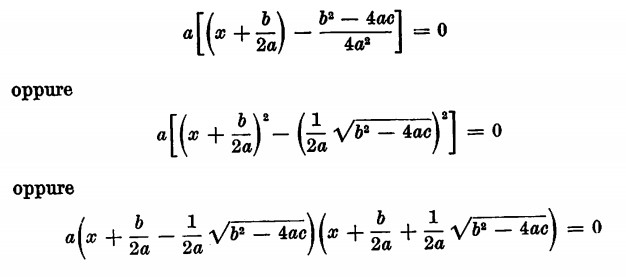
Se uno dei fattori è nullo, anche il primo membro è nullo quindi l’equazione ammette soltanto due soluzioni
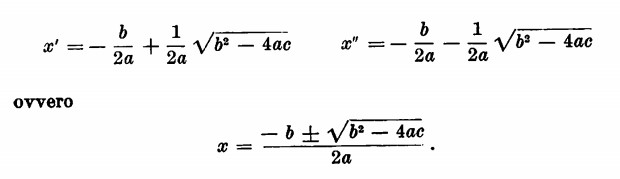
È interessante notare che ove i coefficienti a e e risultino di segno contrario il loro prodotto (ac) risulta negativo (— 4ac è dunque positivo e l’espressione b2 — 4ac è pertanto positiva). L’equazione ammetterà quindi due radici distinte. A tale quantità b2 — 4ac (il cui segno permette di distinguere, tra le equazioni che hanno due radici, quelle che ne hanno una e quelle che non ne hanno affatto) si dà il nome di discriminante dell’equazione stessa. Infine in certe equazioni il coefficiente b risulta il doppio di un numero semplice e lo scriveremo b = 2b’. La formula di risoluzione si scriverà allora:
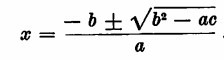
La quantità sotto il segno di radice risulta essere il quarto del discriminante.
Interessanti applicazioni delle equazioni si hanno nella misura dei volumi (capacità). Poniamo d’avere infatti nella credenza tutta una serie di scatole, conservate gelosamente da nostra moglie — attirata, si potrebbe giurare, dalle variopinte etichette — e immaginiamo che noi si voglia adoperarne qualcuna, che so, per riporci del tabacco.
Apriamo lo sportello della credenza e osserviamo che ve ne sono di rettangolari e di cubiche. Dovendo scegliere dal punto di vista della migliore utilizzazione possibile del materiale, tra una scatola rettangolare e una cubica, quest’ultima, a parità di volume, è infatti la costruzione più economica.
Considerata S l’area totale avremo la seguente formula:
S = 2b2 + 4bh
b = lunghezza del lato base
h = altezza.
La formula che ci dà il volume, ovvero la capacità, è V = b2h.
Queste due formule possono essere considerate come equazioni in cui S rappresenta una costante mentre b e h sono delle variabili o incognite che dir si voglia. Due equazioni e tre variabili quindi; è poi senz’altro possibile ridurle a una equazione con due variabili:
(il massimo o minimo valore di V lo si ha allorché l’incremento è pari a 0) pertanto
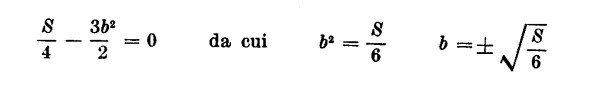
il massimo volume si ha allorché b è pari a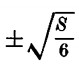 
. Nel medesimo tempo
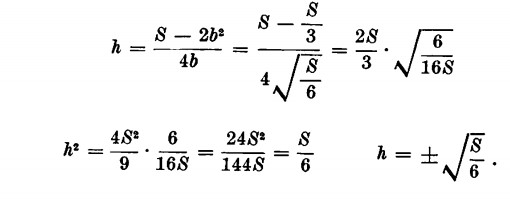
Osserviamo che i valori ottenuti di b e di h sono uguali: .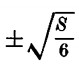
Ne deriva che il massimo volume con la minore superficie si ha quando b è uguale a h. La nostra scatola avrà quindi la forma di un cubo.