Oltre alle frazioni normali, che si indicano con coppie numeriche del tipo 
esistono anche le frazioni ‘decimali’. Le frazioni decimali non so-
no un insieme speciale di frazioni, sono le frazioni normali scritte secondo il sistema decimale. Tale metodo di scrittura si basa sull’idea di estendere il sistema posizionale decimale ‘a destra della virgola’, cioè per numeri o gruppi di numeri più piccoli dell’unità.
Così come il primo posto a sinistra della virgola è assegnato alle unità, il secondo alle decine, e così di seguito, allo stesso modo il primo posto a destra della virgola è assegnato ai decimi, il secondo ai centesimi, il terzo ai millesimi, e così via.
L’immagine che suggerisce la scrittura in frazioni decimali ricorda un po’ la retta numerica: anche qui come allora, il ‘centro’ (nella retta numerica il punto zero, nella frazione decimale la virgola che separa le unità dai decimi) è ‘fisso’, mentre la figura si può estendere a piacere verso sinistra o verso destra.
In effetti, la peculiarità della scrittura decimale con la virgola consiste nell’estrema libertà con cui si può procedere sia a sinistra della virgola, vale a dire nel dominio del ‘grande’, sia a destra della virgola, vale a dire nel dominio del ‘piccolo’.
Di tale possibilità di ampliamento arbitrario delle frazioni decimali si fa uso quando si trasformano le frazioni scritte sotto forma di coppie numeriche in frazioni decimali. Le frazioni decimali si ottengono, infatti, considerando le frazioni scritte in forma di coppie di numeri come divisioni e calcolandone poi il valore.
Il modo come si esegue una divisione lo si impara a scuola. Ad esempio,
Il metodo consiste nello scomporre il dividendo in addendi parziali e nel dividere singolarmente tali addendi, in base alla legge di distributività:
3948 = 3500 + 420 + 28.
Finché l’operazione non è terminata, i resti vengono aggiunti di volta in volta agli addendi rimanenti, ovvero, quando il dividendo è ‘esaurito’, si ha un resto finale:
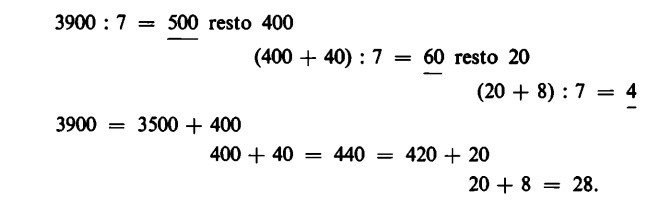
La scrittura in decimali con l’impiego della virgola ci permette di ‘calcolare’ esattamente il valore delle frazioni, in modo da evitare l’assunzione di resti o di frazioni proprie.
Possiamo così calcolare il quoziente di divisioni che non danno risultati interi, come 39 : 7, senza limitarci al risultato ‘5 con resto 4’ oppure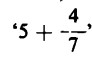 
: è sufficiente pensare il dividendo, il numero intero 39, nella
forma 39, 0000…
A questo punto possiamo ‘abbassare’ anche gli zero e proseguire indefinitamente la divisione anche sulla destra della virgola quanto si vuole:
La divisione non si può eseguire senza resto, ovvero non può essere portata a termine. Accade tuttavia un fatto notevole: dopo alcune operazioni nel quoziente compaiono delle cifre che si ripetono periodicamente, come nella filastrocca « C’era una volta un re, seduto sul sofà, chiamò il suo servo e disse: ‘Raccontami una storia’, e il servo incominciò: C’era… » Diciamo allora che la frazione decimale è ‘periodica’.
A questo punto si può mostrare che ogni numero razionale, vale a dire ogni coppia numerica che sia intesa come frazione e sia inoltre una divisione senza soluzione intera (come ad esempio: 35 : 7), può essere trasformata in una frazione decimale avente un numero finito di decimali oppure in una frazione decimale che ha un numero di decimali non finito, ma è periodica:
