Cosa Sono le Variabili in Matematica – Guida

In questa guida spieghiamo cosa sono le variabili in matematica.

Quando abbiamo parlato dei numeri e delle loro possibili operazioni, abbiamo molto spesso seguito questo procedimento: abbiamo disegnato una figura costituita da un ‘certo’ numero di trattini e poi abbiamo scritto, ad esempio, l’espressione: a + b = c.
Che cosa significano queste lettere? Chiaramente esse stanno per sequenze di trattini e pertanto — in forza dell’astrazione che porta da figure numeriche o cifre a numeri — designano numeri.
Ma che numeri sono? Quando si operava su sequenze di trattini non aveva importanza la quantità dei trattini. Se ne disegnavano 5, 7, o 11 ad arbitrio. Infatti le proprietà che volevamo dimostrare, per esempio la commutatività dell’addizione, dovevano risultare indipendenti dal numero occasionale dei trattini; in altri termini, la loro validità non doveva essere legata alla scelta casuale di determinati numeri, bensì doveva essere provata per numeri ‘qualsiasi’. Nessuna delle nostre dimostrazioni poteva dunque dipendere dal numero occasionale dei trattini che costituivano le figure che servivano ai fini della nostra dimostrazione. Un caso parallelo a questo l’abbiamo nella geometria, ove si fa oggetto delle nostre considerazioni un triangolo ‘qualsiasi’, irregolare al massimo (senza angoli uguali, senza lati uguali, senza angoli retti, ecc.), e in riferimento a quello si dimostra una determinata proprietà che vale per tutti i triangoli.

Le lettere a, b, c, . . non sono altro che abbreviazioni linguistiche per figure costituite da un numero qualunque di trattini.
Come alla figura I associamo il segno I, alla figura , I I il segno 2, alla figura I I I il segno 3 e così di seguito, così associamo a una figura ‘qualunque’, costituita da trattini, una lettera dell’alfabeto.
Chiamiamo queste lettere, che rappresentano numeri qualsiasi, variabili. Tale parola ha, a rigore, lo stesso significato del termine ‘mutabile’. Una simile traduzione può ingenerare, tuttavia, delle ambiguità, in quanto l’espressione ‘mutabile’ suggerisce l’idea, ovvia ma fuorviante, che il numero rappresentato da a, b, c, . . . venga continuamente mutato, come se con la lettera a si volesse indicare in questa riga 7, in quella dopo 5 e nell’altra ancora 11.
Non è però così. Infatti, in un determinato contesto una data lettera designa sempre lo stesso numero. Solo che questo numero non deve essere fissato una volta per tutte. Esso può cambiare da contesto a contesto e per questo è un numero ‘qualunque’, un numero ‘arbitrario’. Non si tratta, tuttavia, di un numero ‘qualunque’ in senso assoluto: infatti viene sempre fissato un dominio, all’interno del quale deve trovarsi il numero designato dalla lettera. Per esempio, vengono poste restrizioni come le seguenti: ‘a sia un numero intero’, ‘a sia diverso da 0’, ‘a sia positivo’, ‘a sia minore di 12’, ecc. Ma tali determinazioni dei ‘campo di variabilità’ non snaturano il concetto di variabile: all’interno di un dato contesto di derivazioni o d’altro genere, una lettera variabile designa sempre un numero ‘qualsiasi’, purché costante all’interno del contesto stesso.

Oggi, al posto della parola ‘variabile’, si usano volentieri termini come `detentore di posto’ o ‘posto libero’, termini questi che stanno a significare come una variabile non sia che una ‘lacuna nel testo’, in cui può essere inserito un numero. Si potrebbe dunque contrassegnare una variabile, anziché con una lettera dell’alfabeto, con uno ‘spazio vuoto’, per esempio con un trattino orizzontale -, oppure con due puntini .. , tutte scritture queste che suggeriscono l’idea di riempire il vuoto. È questo il motivo per cui si è paragonato, giustamente del resto, un testo matematico pieno di variabili a un questionario in cui sono previsti degli spazi liberi per l’inserimento dei dati. Il paragone con un questionario è, anzi, molto appropriato. Infatti, quando si distribuisce un questionario ad alcuni cittadini, chi lo distribuisce si aspetta che ognuno degli interpellati riempia il questionario con dati diversi; per esempio gli interpellati dichiareranno date di nascita diverse. Però i dati dichiarati da ogni singolo interpellato dovranno essere univocamente determinati in quanto riferiti alla stessa persona (sempre che le risposte siano veritiere).

La persona Taldeitali (`Taldeitali’ è anch’essa una variabile!) riempirà la voce « nato il . .  » con una data precisa.
Si può dunque dire: per chi distribuisce il questionario, la riga « nato il .. » è un posto vuoto da riempire con date ‘qualsiasi’, cioè con le date di nascita dei cittadini tuttora viventi. Al contrario, dal punto di vista del cittadino che compila il questionario, la riga « nato il . . » è un posto vuoto da riempire con un numero ben preciso.

Passando alla matematica: per svolgere una dimostrazione possiamo usare dei numeri qualsiasi scelti all’interno del dominio richiesto; però durante la dimostrazione una lettera designa sempre lo stesso numero.
Poiché le variabili non sono nient’altro che ‘posti vuoti’, si potrebbe in effetti lavorare semplicemente con essi senza scomodare le lettere dell’alfabeto. C’è però un motivo di carattere pratico che suggerisce di indicare tali posti vuoti con lettere dell’alfabeto: di solito, infatti, dobbiamo lavorare con parecchi numeri da sostituire con variabili. È necessario pertanto distinguere le singole variabili, cosa difficilmente realizzabile senza usare le lettere dell’alfabeto. Per sottolineare il carattere di ‘posti vuoti’ delle variabili, possiamo, dunque, lavorare con figure chiuse, per esempio  nelle quali si possano inserire dei segni numerici.
Ancora meno plausibile di ‘variabile’ è il termine ‘incognita’, termine questo proveniente dall’uso invalso nel calcolo delle equazioni. Non è detto infatti che il numero indicato con una variabile sia in ogni caso sconosciuto. Se, ad esempio, abbiamo la seguente relazione:

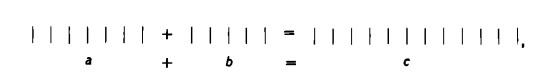
non ci sono per niente sconosciuti i numeri rappresentati dalle variabili a, b e c. Basta contare i trattini per vedere che a corrisponde a 7, b a 5 e c a 12. Però, per la nostra dimostrazione, è indifferente che le variabili abbiano i valori ora scritti o altri, la loro interpretazione è abritraria.
In matematica, tuttavia, sono molto poche le derivazioni che utilizzano solo variabili. È vero, ad esempio, che la legge della commutatività dell’addizione si può esprimere attraverso la sequenza di segni a + b = b + a,
costituita da = e lettere dell’alfabeto. Ma basta aver a che fare con concetti come ‘numero pari’, o ‘quadrato di un numero’, per dover scrivere 2a o a². In matematica esistono dunque molte espressioni in cui ricorrono oltre a variabili anche cifre. L’espressione ‘2a’ significa dunque: ‘un numero naturale à raddoppiato, vale a dire un numero pari, cioè un numero divisibile per 2’ (se, al contrario, vogliamo designare un prodotto di due qualsiasi numeri interi, usiamo per ambedue i fattori le variabili: ab).
Chiamiamo costanti (in contrapposizione alle variabili) quei segni, come 1, 2, . . . , 9, . . . , 374, . . . , 5892, .. . , che indicano numeri il cui valore è fisso anche in calcoli che contengono variabili. Costanti sono anche quei segni costituiti da una lettera per ragioni di brevità linguistica, ma che designano sempre un numero determinato. Il caso più conosciuto di tali costanti è il segno per il numero π, rapporto tra la circonferenza e il diametro di un cerchio, coincidente con 3, 14159 . .. Per ragioni di brevità, si indica con la lettera dell’alfabeto greco π. Anche espressioni come e simili designano naturalmente delle costanti.