In questa guida spieghiamo come si calcola il minimo comune multiplo.
Il minimo comune multiplo (anche: m.c.m.) è il più piccolo dei multipli comuni a due o più numeri diversi da zero. I multipli di un numero sono infiniti. Per costruire i multipli di un numero è sufficiente moltiplicare questo per 0, 1, 2, 3, … ecc. Dati due numeri come 2 e 3 i loro multipli saranno rispettivamente:

il numero sottolineato è il multiplo comune più piccolo, il quale è maggiore di entrambi i numeri considerati (cosa che non potrebbe essere altrimenti dato che si tratta di un multiplo).
Possiamo anche dire che se tra due o più numeri ve n’è uno divisibile per gli altri, questo è il minimo comune multiplo dei numeri dati. Nel nostro caso, dati i numeri 2, 3, 6, l’ultimo di questi, essendo divisibile per gli altri due, è il loro m.c.m.
Quando si hanno tre o più numeri, bisogna dapprima trovare il m.c.m. di due di essi, poi col m.c.m. trovato e un altro dei numeri considerati si ricerca un secondo m.c.m. e così via sino ad aver esaurito tutti i numeri.
Il m.c.m. degli ultimi due numeri è quello desiderato. Se due o più numeri vengono moltiplicati o divisi per uno stesso numero, anche il loro m.c.m. viene moltiplicato o diviso (sempre nel caso che tale numero sia un divisore comune dei numeri presi in considerazione) per tale numero.
Si può trovare il m.c.m. tra due o più numeri usando il metodo dei fattori primi, cioè scomponendo i numeri dati in fattori ed eseguendo il prodotto dei fattori primi (comuni e non comuni) al massimo esponente.
Vediamo un semplice esempio pratico.
Due treni passano davanti a un casello rispettivamente ogni 6 e ogni 8 ore.
Supposto che il casellante li abbia visti passare contemporaneamente alle ore 22 di un dato giorno, tra quante oro i treni torneranno a incrociarsi?
Il numero delle ore che trascorrerà prima del passaggio simultaneo, sarà dato dal m.c.m. di 6 e 8, cioè 24. Alle 22 dell’indomani i treni sfrecceranno di nuovo insieme davanti agli occhi del casellante.
Un altro calcolo. Sia da ricercare il m.c.m. tra le frazioni:
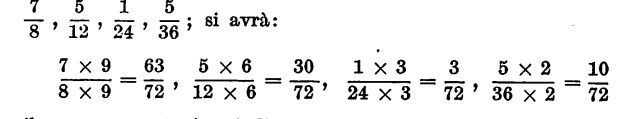
il m.c.m. cercato è quindi 72.